【1462. 课程表 IV】

news2024/10/6 6:41:35

来源：力扣（LeetCode）

描述：

你总共需要上 numCourses 门课，课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ，其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程，你必须先选 ai 课程。

有的课会有直接的先修课程，比如如果想上课程 1 ，你必须先上课程 0 ，那么会以 [0,1] 数对的形式给出先修课程数对。

先决条件也可以是间接的。如果课程 a 是课程 b 的先决条件，课程 b 是课程 c 的先决条件，那么课程 a 就是课程 c 的先决条件。

你也得到一个数组 queries ，其中 queries[j] = [uj, vj]。对于第 j 个查询，您应该回答课程 uj 是否是课程 vj 的先决条件。

返回一个布尔数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

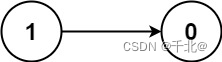
输入：numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

输入：numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：

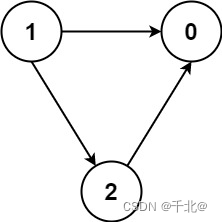
输入：numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

提示：

2 <= numCourses <= 100
0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
prerequisites[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
每一对 [ai, bi] 都不同
先修课程图中没有环。
1 <= queries.length <= 10⁴
0 <= ui, vi <= n - 1
ui != vi

方法一：广度优先搜索 + 拓扑排序

思路与算法

题目给出 numCourses 门课（编号从 0 开始），并给出了一个长度为 n 的课程之间的制约关系数组 prerequisite ，其中 prerequisite[i] = [ai, bi] 表示在学习课程 bi 之前必须要完成课程 ai 的学习，即课程 ai 为 bi 的先决条件。我们可以将上述条件构建一张有向图——将每一个课程看作一个点（课程编号即为点的编号），每一个制约关系 prerequisite[i] = [ai,bi] 对应一条从点 ai 指向 bi 的有向边，并且题目保证了这样构建出来的图不存在环。

现在有 m 个查询 queries，其中对于第 i 个查询 queries[i] = [ui,vi]，我们需要判断课程 ui 是否是课程 vi 的直接或间接先决条件。我们创建一个 numCourses×numCourses 的矩阵 isPre，其中 isPre[x][y] 表示课程 x 是否是课程 y 的直接或间接先决条件，若是则 isPre[x][y] = True，否则 isPre[x][y] = False。在完成 isPre 计算后，我们对于每一个查询就可以在 O(1) 时间得到结果。对于 isPre 的计算，我们可以通过「广度优先搜索」+「拓扑排序」来对矩阵 isPre 进行计算：

首先我们需要计算有向图中每一个节点的入度，并对入度为 0 的节点加入队列。然后只要队列非空，就进行以下操作：

取出队列队首元素，同时，将这个节点及其所有前置条件节点设置为所有后续节点的前置条件节点，然后对每一个后续节点入度进行 −1 操作，若操作后的节点入度为 0，则继续将该节点加入队列。

「拓扑排序」结束后，矩阵 isPre 计算完毕，然后我们遍历每一个查询，根据矩阵 isPre 即可得到每一个查询的结果。

代码：

class Solution {
public:
    vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
        vector<vector<int>> g(numCourses);
        vector<int> indgree(numCourses, 0);
        vector<vector<bool>> isPre(numCourses, vector<bool>(numCourses, false));
        for (auto& p : prerequisites) {
            ++indgree[p[1]];
            g[p[0]].push_back(p[1]);
        }
        queue<int> q;
        for (int i = 0; i < numCourses; ++i) {
            if (indgree[i] == 0) {
                q.push(i);
            }
        }
        while (!q.empty()) {
            auto cur = q.front();
            q.pop();
            for (auto& ne : g[cur]) {
                isPre[cur][ne] = true;
                for (int i = 0; i < numCourses; ++i) {
                    isPre[i][ne] = isPre[i][ne] | isPre[i][cur];
                }
                --indgree[ne];
                if (indgree[ne] == 0) {
                    q.push(ne);
                }
            }
        }
        vector<bool> res;
        for (auto& query : queries) {
            res.push_back(isPre[query[0]][query[1]]);
        }
        return res;
    }
};

时间 232ms 击败 46.33%使用 C++ 的用户
内存 58.08MB 击败 61.78%使用 C++ 的用户
复杂度分析

时间复杂度：O(numCourses²+n+m)，其中 numCourses 为课程数，n 为题目给出的先决条件的数目，m 为题目给出的查询数，其中通过计算矩阵 isPre 的时间复杂度为 O(numCourses²)，构建有向图的复杂度为 O(numCourses+n)，处理每一个查询的复杂度为 O(1)，共有 m 个查询，所以总的查询时间复杂度为 O(m)。
空间复杂度：O(numCourses²+n)，其中 numCourses 为课程数，n 为题目给出的先决条件的数目，主要为构建有向图和矩阵 isPre 的空间开销。注意返回值不计入空间复杂度。

方法二：深度优先搜索 + 拓扑排序

思路与算法

「方法一」中「拓扑排序」的实现同样可以通过「深度优先搜索」来实现。与「广度优先搜索」计入每一个点的出度不同，通过「深度优先搜索」需要记录每一个点是否被访问，我们用 vi[x] 来表示课程 x 是否被访问，初始时为 False。

我们从编号小到大遍历全部节点，若节点 i 未被访问，则进入「深度优先搜索」流程：

若当前节点 x 已被访问，则直接返回。
若当前节点 x 未被访问，将访问状态设为已访问，然后继续对其全部后继节点递归进行「深度优先搜索」流程。将节点 x 置为其每一个后继节点 y 的先决条件，有 isPre[x][y] = True，以及对于每一个以 y 为先决条件的节点 t，节点 x 同样为 t 的先决条件，有 isPre[x][t] = True。

遍历完成后，「拓扑排序」完成，矩阵 isPre 计算完毕，然后我们遍历每一个查询，根据矩阵 isPre 即可得到每一个查询的结果。

代码：

class Solution {
public:
    void dfs(vector<vector<int>>& g, vector<vector<bool>>& isPre, vector<bool>& vi, int cur) {
        if (vi[cur]) {
            return;
        }
        vi[cur] = true;
        for (auto& ne : g[cur]) {
            dfs(g, isPre, vi, ne);
            isPre[cur][ne] = true;
            for (int i = 0; i < isPre.size(); ++i) {
                isPre[cur][i] = isPre[cur][i] | isPre[ne][i];
            }
        }
    }

    vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
        vector<vector<int>> g(numCourses);
        vector<bool> vi(numCourses, false);
        vector<vector<bool>> isPre(numCourses, vector<bool>(numCourses, false));
        for (auto& p : prerequisites) {
            g[p[0]].push_back(p[1]);
        }
        for (int i = 0; i < numCourses; ++i) {
            dfs(g, isPre, vi, i);
        }
        vector<bool> res;
        for (auto& query : queries) {
            res.push_back(isPre[query[0]][query[1]]);
        }
        return res;
    }
};

时间 212ms 击败 55.98%使用 C++ 的用户
内存 57.84MB 击败 73.75%使用 C++ 的用户
复杂度分析

时间复杂度：O(numCourses²+n+m) ，其中 numCourses 为课程数，n 为题目给出的先决条件的数目，m 为题目给出的查询数，其中计算矩阵 isPre 的时间复杂度为 O(numCourses²) ，构建有向图的复杂度为 O(numCourses+n)，处理每一个查询的复杂度为 O(1)，共有 m 个查询，所以总的查询时间复杂度为 O(m)。
空间复杂度：O(numCourses²+n) ，其中 numCourses 为课程数，n 为题目给出的先决条件的数目，主要为构建有向图和矩阵 isPre 的空间开销。注意返回值不计入空间复杂度。
author：力扣官方题解