一、堆的概念及结构

1、什么是堆

堆就是以二叉树的顺序存储方式来存储元素，同时又要满足父亲结点存储数据都要大于儿子结点存储数据或者父亲结点数据都要小于儿子结点数据的一种数据结构。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

2、堆的性质

• 堆中某个节点的值总是不大于或不小于其父节点的值
• 堆总是一棵完全二叉树
• 堆的根节点总是极值

3、堆的结构及分类

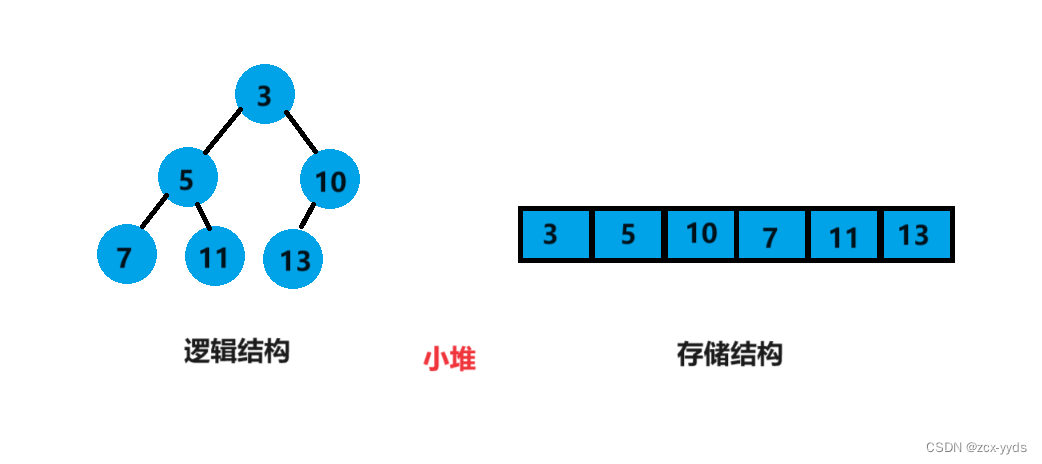
小堆：所有的双亲结点都小于孩子节点，根节点最小

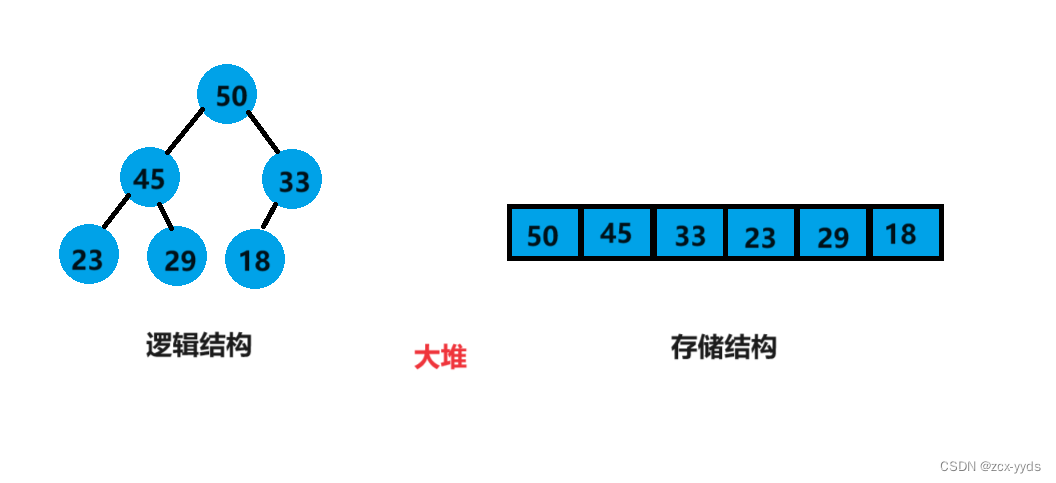
大堆：所有的双亲结点都大于孩子节点，根节点最大

二、堆的创建

后面代码用到的堆结构体：

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

重要关系：

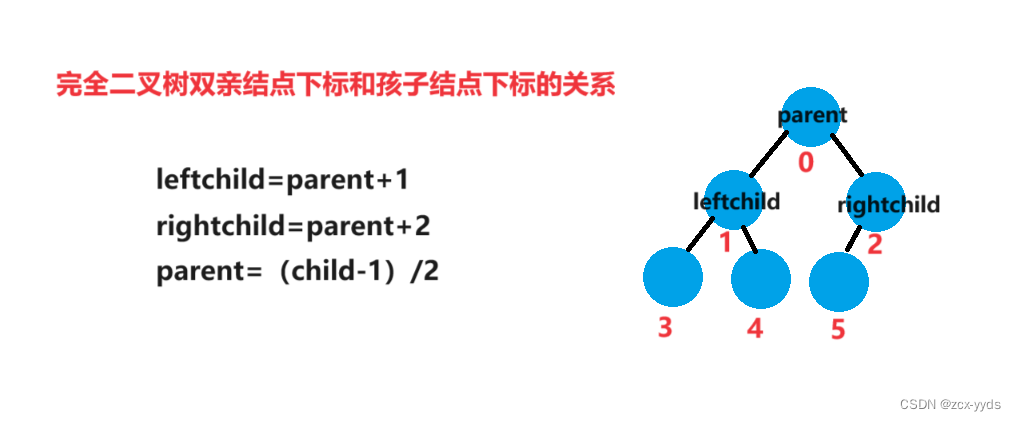
1、堆向下调整算法

例如有一个数组：

int arr[] = {27,15,19,18,28,34,65,49,25,37};

将这个数组逻辑上看成一颗完全二叉树，通过从根节点开始的向下调整算法可以把它调整成一个大堆或小堆。
向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

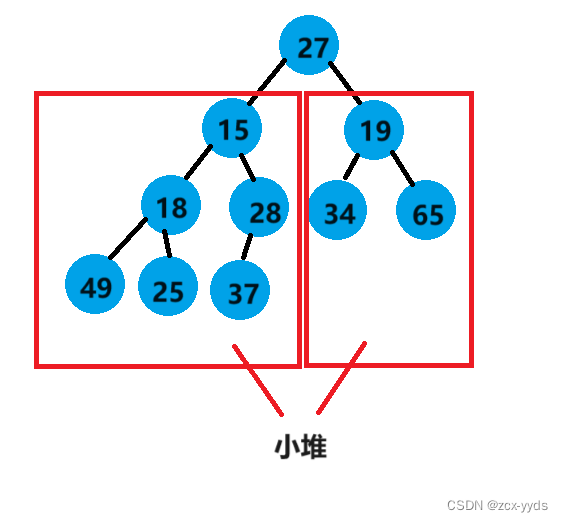
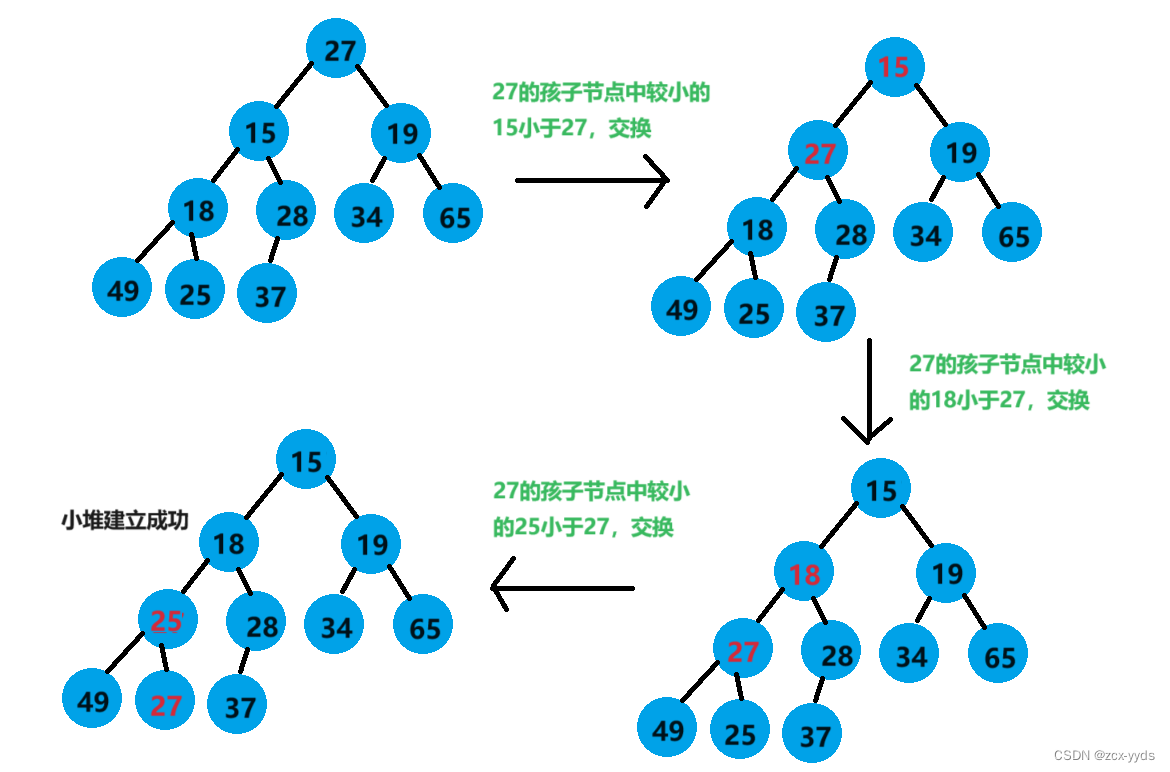
以下代码是用向下调整法调整为小堆：

//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
	//先默认左孩子是较小的
	int child = parent * 2 + 1;

	while (child < n)
	{
		//找出左右孩子中较小的
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		//孩子节点更小则交换
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

2、堆向上调整算法

例如对如下小堆：

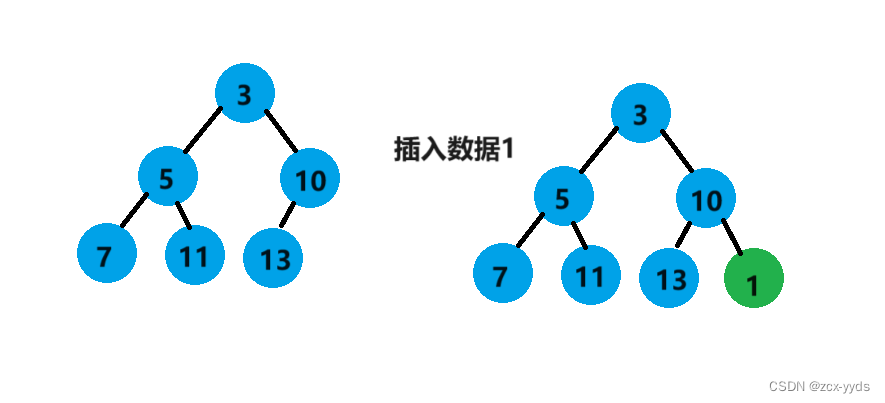
该小堆插入数字1后就不是小堆了，需要用从这个元素开始的向上调整算法对它进行调整。

向上调整有一个前提：前面的元素是堆

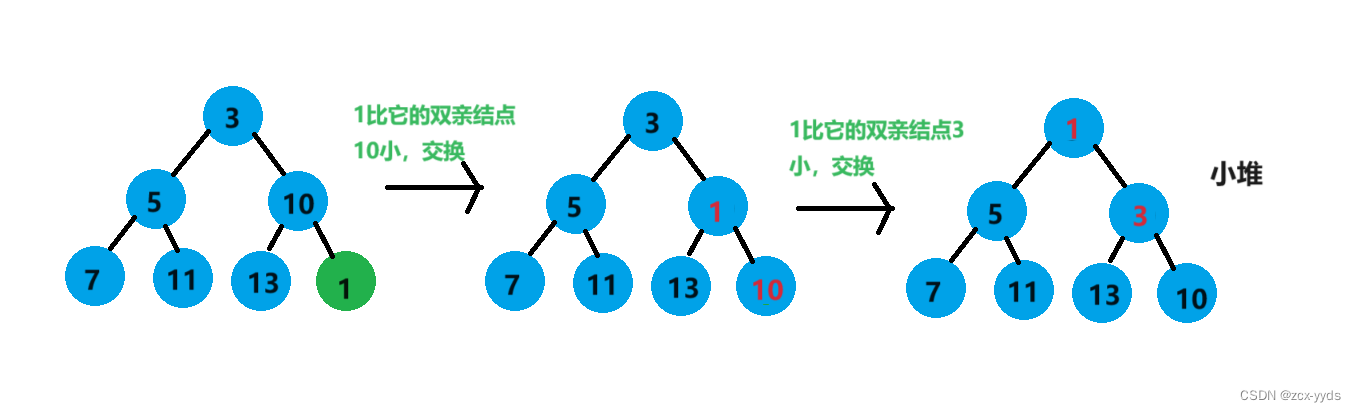
以下代码是用向上调整法调整为小堆：

//向上调整
void AdjustUp(HPDataType* a, int child)
{
	//找出双亲的下标
	int parent = (child - 1) / 2;

	while (child>0)
	{
		//孩子结点比双亲小则交换
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

3、堆的创建

向上调整算法和向下调整算法想要使用都有前提，对于一个数组，想要让它在逻辑结构上可以看作一个堆，那就可以先让它满足这两种算法其中一种的条件，然后进行调整即可。

对于单个结点来说既可以看作大堆也可以看作小堆，所有便可以通过向上调整算法依次对数组元素进行调整，那进行调整的元素前就一定是堆，满足条件，以下为该方法的代码：

// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
	assert(hp);
	assert(a);

    //开辟存放堆元素的内存空间
	hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (hp->a == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	hp->size = n;
	hp->capacity = n;

    //将数组元素复制到堆中存放元素的内存空间内
	memcpy(hp->a, a, sizeof(HPDataType) * n);

    //从下标1开始进行向上调整
	for (int i = 1; i < n; i++)
	{
		AdjustUp(hp->a, i);
	}
}