世界上最遥远的距离，不是生与死的距离，不是天各一方，而是，我就站在你的面前，你知道我爱你。 —— 木子李

学习数据科学中距离的度量方法，这里有一篇来自知乎的中文博文可以阅读，原文中有的内容就不赘述了，以下只是我对这些距离衡量方法的提炼、思考和理解。

距离本身的意思是，两个地点之间相距的距离，但被延申后距离应该指两个对象之间相异的程度（即有多大的不同或相同），差异不同于远近，因此我不认为计算机中的许多术语翻译成距离是合适的，距离一词容易让人联想到现实中的距离，差异比距离更合适，例如余弦距离，应该叫余弦差异，余弦相似度的翻译是取“差异”的反面。

一、欧式距离(Euclidean Distance)

$$D(x,y)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$

文章中说：“欧式距离不是尺度不变的，这意味着所计算的距离可能会根据特征的单位发生倾斜”，根据上述公式，即便是同样的距离如100cm和1m，单位为cm所计算出的数值会比单位m“大100倍，这就是根据特征的单位发生倾斜的含义的具体表现之一。

文中又说：“随着数据维数的增加，欧式距离的作用就越小。这与维数灾难（curse of dimensionality）有关。”，这里我貌似理解，但没有实际的例子可供举例。

二、余弦相似度(Cosine Similarity)

$$D(x,y)=cos(\theta )=\frac{x\cdot y}{||x||||y||}$$

当数据是高维，且向量的大小不重要时，使用余弦相似度。

三、汉明距离(Hamming Distance)

又叫海明距离，可用于计算机网络传输时的错误纠正/检测，此处需复习计算机网络。

四、曼哈顿距离(Manhattan Distance)

$$D(x,y)=\sum _{i=1}^k|x_i-y_i|$$

“当数据有离散或二进制属性时，此距离似乎很起效。”

五、切比雪夫距离(Chebyshev Distance)

切比雪夫距离定义为两个向量在任意坐标维度上的最大差值。但是它为什么又被称作棋盘距离？

国王可以上下左右斜着走，如果将国王所处位置视作原点，其向量是(0,0)，而从该点出发到其它棋格的向量视作(x,y)，套用刚刚的“两个向量在任意坐标维度上的最大差值”，则可以得到下面这张图，用来展示国王走到其它棋格的最小步数，来自百度百科。

实践中，切比雪夫距离经常用于仓库物流，道理也简单，机械臂可以同时沿着x轴与y轴移动。

六、闵可夫斯基距离(Minkowski Distance)

$$D(x,y)=(\sum _{i=1}^n{|x_i-y_i|}^p{)}^{\frac{1}{p}}$$

这么美的公式，会不会有什么直观的几何含义？ 换言之，这公式可视化出来是什么样子？在维度是二维(对于上面这个公式就是$n=2$)的前提下，图形长这个样子^[4]，蓝色线的含义是，蓝线上的点与原点$O$之间的距离，套用上面的公式时，其计算值都一样，类似于等高线，最显眼的形状分别是 $p=1,2,\infty$ 。

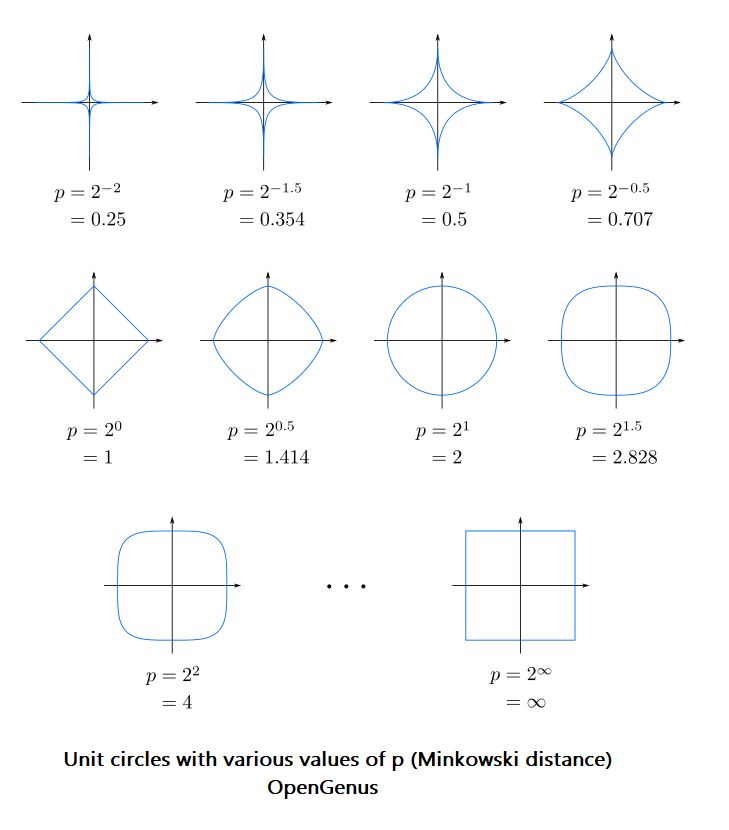
其中，有点意思的是$p=\infty$的推导过程，我们只取两个点，一个点是$(x,y)$，一个点是$(0,0)$，维度$n=2$，由于计算时带了绝对值，所以只考虑第一象限$(x>0,y>0)$，其余象限可以用对称性推导出来。
$$\begin{gathered} D=\underset{p\to \infty }{\lim }[(x-0{)}^p+(y-0{)}^p{]}^{\frac{1}{p}} \\ =\underset{p\to \infty }{\lim }(x^p+y^p{)}^{\frac{1}{p}} \\ \stackrel{y=ax}{=}\underset{p\to \infty }{\lim }[x^p+(ax{)}^p{]}^{\frac{1}{p}} \\ =\underset{p\to \infty }{\lim }[(1+a^p)x^p{]}^{\frac{1}{p}} \\ =\underset{p\to \infty }{\lim }(1+a^p{)}^{\frac{1}{p}}x(a>0) \end{gathered}$$
分类讨论：

(1)当$a=1$时。$D={\lim }_{p\to \infty }(2x^p{)}^{\frac{1}{p}}={\lim }_{p\to \infty }{2}^{\frac{1}{p}}x=x$，此时 $y=ax=x$。

符号 $p$ 作为自由变量，大多数人的眼睛应该是看不习惯的，下面，回归到纯粹的高等数学习题上，将符号 $p$ 替换成符号 $x$ ，久违的高数习题的感觉扑面而来，请求以下式子的极限值
$$\underset{x\to \infty }{\lim }(1+a^x{)}^{\frac{1}{x}}(a>0,a\ne 1)$$
(2)当$a<1$时。令$a^x=u$，则$x=lo{g}_{a}u$，原式等价于求
$$\begin{gathered} \underset{u\to 0}{\lim }(1+u{)}^{\frac{1}{{\log }_{a}u}} \\ =\underset{u\to 0}{\lim }(1+u{)}^{\frac{lna}{lnu}} \\ =\underset{u\to 0}{\lim }[(1+u{)}^{\frac{1}{lnu}}{]}^{lna} \\ =\underset{u\to 0}{\lim }[e^{ln(1+u{)}^{\frac{1}{lnu}}}{]}^{lna} \\ =\underset{u\to 0}{\lim }[e^{\frac{ln(1+u)}{lnu}}{]}^{lna} \\ \stackrel{洛}{=}\underset{u\to 0}{\lim }[e^{\frac{u}{1+u}}{]}^{lna} \\ =1^{lna} \\ =1 \end{gathered}$$
(3)当$a>1$时。沿用上面的式子
$$\begin{gathered} \stackrel{洛}{=}\underset{u\to \infty }{\lim }[e^{\frac{u}{1+u}}{]}^{lna} \\ =e^{lna} \\ =a \end{gathered}$$
总结：

(1)当$a=1$时。$D=(2x^p{)}^{\frac{1}{p}}=2^{\frac{1}{p}}x=x$，此时 $y=ax=x$。

(2)当$a<1$时，$D=1\cdot x=x$，此时$y=ax<x$。

(3)当$a>1$时。$D=a\cdot x=y$，此时$y=ax>x$。

也就是说，取两个向量在任意坐标维度上的最大差值。这也就是切比雪夫距离，又叫棋盘距离。

闵可夫斯基这属于犯规了，一个公式可以根据不同的参数，把欧氏距离，曼哈顿距离(这词就他发明的)，切比雪夫距离全部包括进去，生的晚还是有好处的。

七、Jaccard Index

$$D(x,y)=1-\frac{|x\bigcap y|}{|x\bigcup y|}$$

文中说：“Jaccard索引经常用于使用二进制或二进制化数据的应用程序中。当你有一个深度学习模型来预测一幅图像(例如一辆汽车)的片段时，Jaccard索引就可以用来计算给出真实标签的预测片段的准确性。同样，它也可以用于文本相似度分析，以衡量文档之间的选词重叠程度。因此，它可以用来比较模式集。”

八、Haversine Distance

$$d=2R\cdot arcsin\left(\sqrt{si{n}^2(\frac{{\phi }_2-{\phi }_1}{2})+cos({\phi }_1)cos({\phi }_2)si{n}^2(\frac{{\lambda }_2-{\lambda }_1}{2})}\right)$$

哈弗辛距离是球面上的两点在给定经纬度条件下的距离，公式的证明见 Distance between the Points on the Earth’s Surface^[5] 一文，链接置于文末。此处可以说一句，嗯，我爱数学。

九、Sørensen-Dice Index

$$D(x,y)=\frac{2|x\cap y|}{|x|+|y|}$$

“它衡量的是样本集的相似性和多样性，通常用于图像分割任务或文本相似度分析。”

References

[1] 一图看遍9种距离度量，图文并茂，详述应用场景！—— 知乎

[2] 9 Distance Measures in Data Science —— 原文

[3] [美]特南鲍姆(Tanenbaum, A.S.)，[美]韦瑟罗尔(Wetherall, D.J.). 计算机网络（第5版）[M].严伟,潘爱民.北京：清华大学出版社，2012.

[4] Minkowski distance [Explained]

[5] Distance between the Points on the Earth’s Surface