在真实的物理世界中，力、热、声、光、电等信号都可能携带了某种信息。我们需要使用数学抽象的方法来建立一套数学模型来作为我们对信号、系统进行描述，这其实就是一个数学建模的过程。 人们把随时间变化或随空间变化的物理信号根据其特性用数学方式来描述，最基本的方法就是写出它的时域解析表示式（函数）或绘出函数的波形。
在信号与系统中，我们对于信号、系统的描述通常使用时间函数，也就是时域来描述、也可以运用时域方法来解决问题。但是我们在实际使用是发现时域的描述简单、但计算是非常复杂的，后面就需要采用频域、复频域、z域等变换方式来快速、简便的解决问题。那就需要引入频谱分析、各种正交变换以及其他方式来描述和研究信号。

• 这节信号、系统的描述都是建立在时域的基础上来叙述的。

本节的思路：

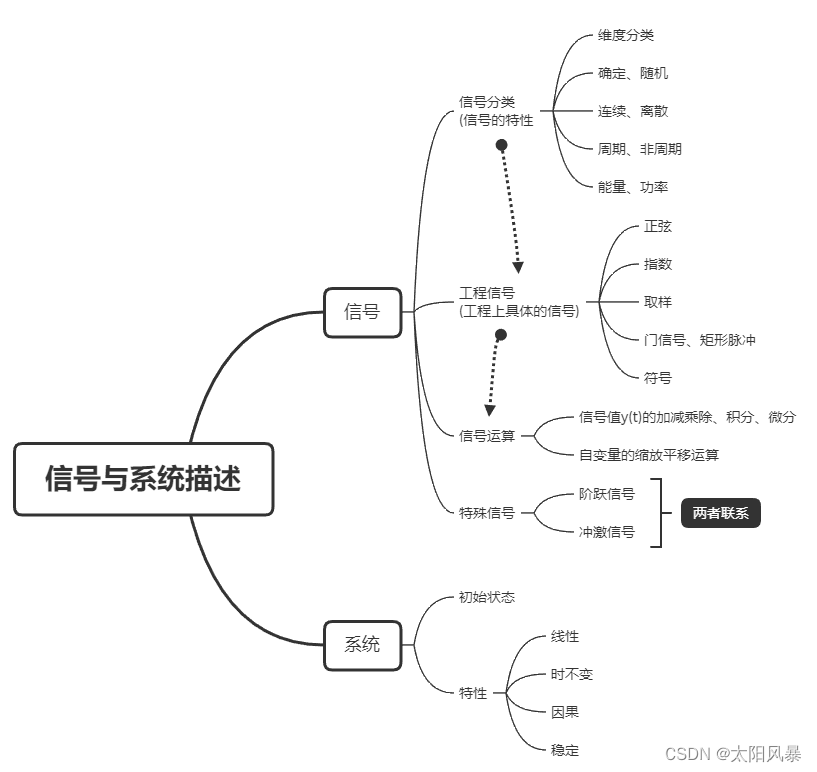
• 因为内容过多，分为两节，这里为下节 包含 信号基本运算、阶跃信号和冲激信号、系统特性及分类
  参考上节内容：
• 信号与系统的描述-上节

一、信号的基本运算

这里涉及到对信号的基本处理，很简单的，里面根据信号的不同，主要是离散和随机信号。

1. 信号的基本运算

1. 加法 、减法

对信号进行加法运算，是将两信号在同一时刻的函数值相加。
减法和加法是一样的，减法是特殊的加法而已。

2. 乘法、除法

对信号进行乘法运算与相加运算相似，是将两信号在同一时刻的函数值相乘。离散信号的相加、相乘运算的示例。相加、相乘运算均是针对同一时刻点的幅值。
除法和乘法一样，除法是特殊的乘法而已。

3. 微分 、差分

1、微分是对连续信号

• 设 f (t)是连续时间信号，则 f (t)对时间 t 的导数
  
  连续时间信号在所有不可导的点都是不连续的。特别是分段连续信号不是在所有的点都是可导的。

2、差分是对离散信号

• 一阶前向差分
  
• 一阶后向差分
  
• 高阶前向差分
  
• 高阶后向差分
  

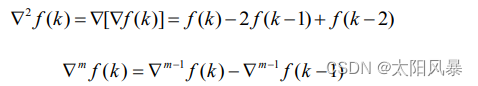
4.积分、迭分

1、积分是对连续信号

• 设 f (t)是连续时间信号，则 f (t)对时间 t 的积分
  

2、迭分是对离散信号

• 迭分运算实际上是一个求累加的过程。
  

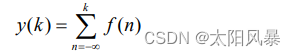
2. 关于时间（自变量）的运算

针对信号的自变量主要有三种运算：位移、反折、尺度变换。

1. 位移

信号 f (t)经过加工后输出的波形形状没有发生改变，与原始信号 f (t)相比仅仅是延迟了 t₀ 时间单位（设 t₀ > 0），则延迟后的信号可表示为 f(t -t₀ ) ，其波形相当于将 f (t)的波形沿着时间 t 轴向右水平移动了 t₀ 个时间单位。f (t + t₀ ) 的波形则相当于把 f (t)的波形沿着时间 t 轴向左水平移动了 t₀ 个时间单位。

• 左加右减 原则

例题

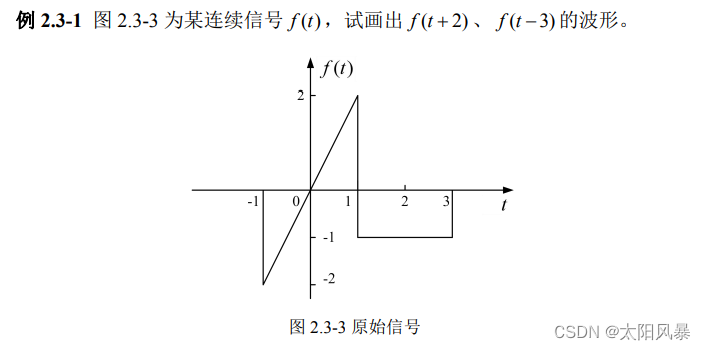
答案

2. 反折

设 f (t)是连续时间信号，信号的反折是将 f (t)的自变量 t 用t 替换，从而得到新的信号 y(t)

• y(t) = f(-t)

例题

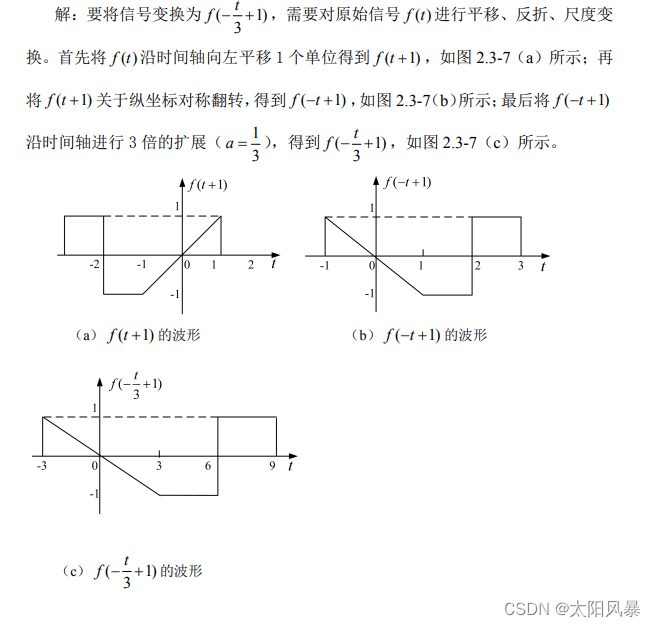
3. 尺度变换

设 f (t)是连续时间信号，对于实数 a ，信号的尺度变换表示将 f (t)的自变量 t 用at 替换，得到新的信号 y(t)

• y(t) = f(at)

若 |a| > 1，对信号 f (t) 进行尺度变换是将原信号 f (t) 沿着横轴方向压缩；若 |a| < 1，对信号 f (t)进行尺度变换是将原信号 f (t)沿着横轴方向展宽。

例题

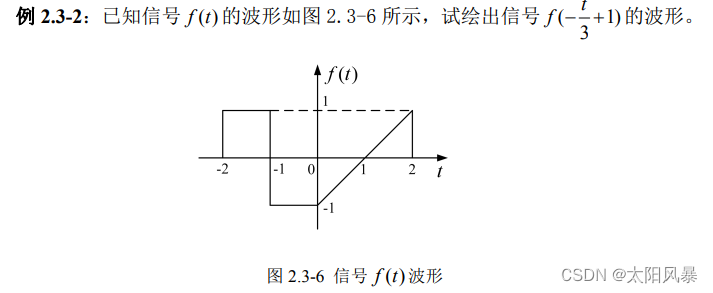
答案

二、阶跃信号与冲激信号

如果信号本身、其导数或积分有不连续点（跳变点），则把该信号称为 奇异信号（或称奇异函数），这里主要介绍两类奇异信号：单位阶跃信号和单位冲激信号。

1. 单位阶跃信号

• 定义
  
• 图像
  
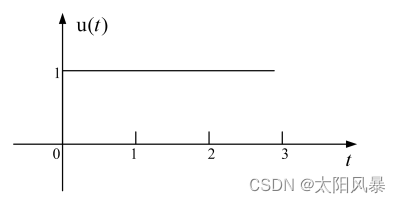
  该信号在t = 0时不同的书有不同的定义，有的书定义u(0) = 0，有的书定义u(0) = 1，还有的书定义u(0) 为 t = 0₊ 和 t = 0_- 的左右极限的平均值，我学习的那本书中不定义该点的值，视为无定义。
• 对阶跃信号u(t)平移 t₀ 个时间单位后可得：
  
• 平移后图像
  

2. 单位阶跃信号的特性

• 单边特性
  f(t) 在(-∞, +∞) 都有值，但是 f(t) * u(t) 后只有 (0, +∞) 后有值，这就是取单边特性
  

• 用阶跃表示矩形脉冲
  两个阶跃信号相互减，就构成了门函数，减的是 u(+) - u(-) 形成门函数
  

3. 单位冲激信号

单位冲激信号可用脉冲信号发生器输出的脉宽极窄而重复周期较长的窄脉冲信号来近似模拟。其物理模型可用一个突然接通又马上断开电源的电路表示。

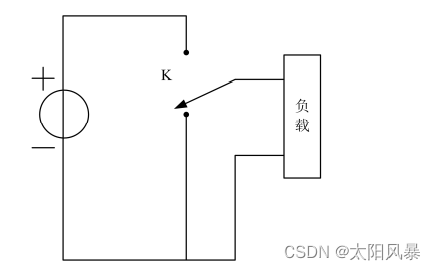
• 定义
  第一个条件表明δ(t)在所有t不为0时取0
  第二个条件就是冲激下的面积为1,因此 δ(t) 有单位面积。

• 图像
  
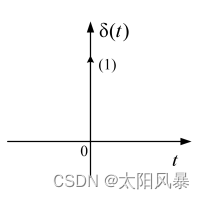
  冲激信号δ(t)可以近似地用一个位于原点处、持续时间为1/A、幅度为A的脉冲来表示，这里，A是一个很大的正值。
  
  单位冲激函数的积分等于单位阶跃函数：
  
  
  单位冲激信号的一阶微分称为冲激偶信号 δ_’
  
  这个信号的特性是 积分特性，其实可以看成上下积分和为0
  
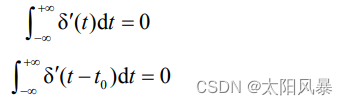
• 经典例题
  

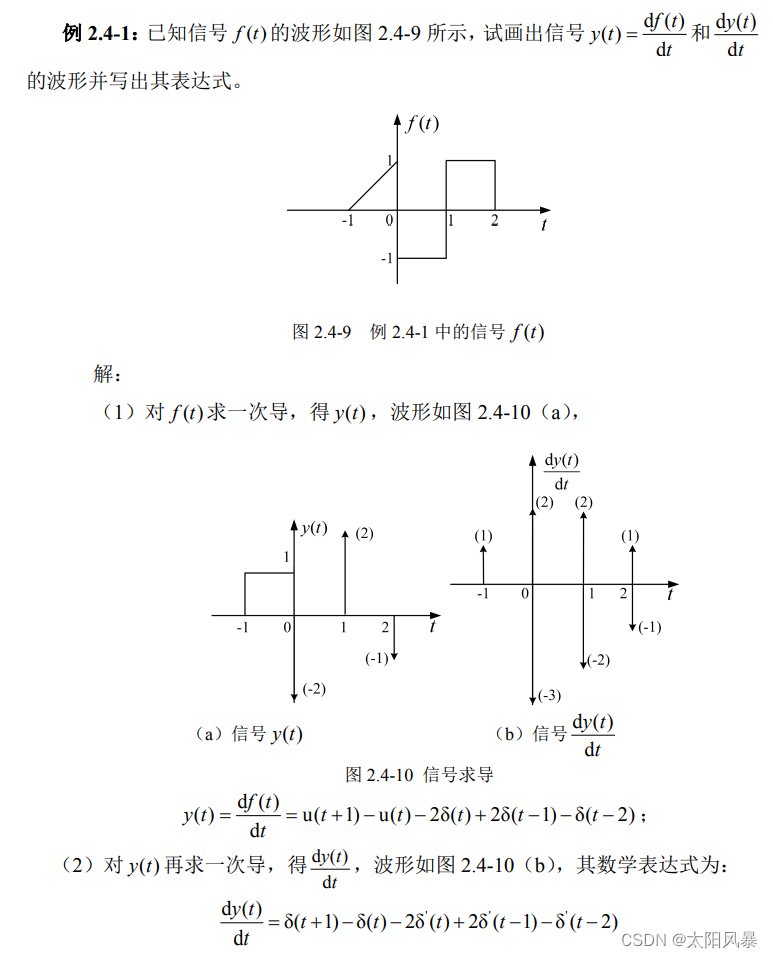
4. 单位冲激信号的性质

• 1、采样特性（筛选特性）
  考虑与任意函数 f (t)相乘，设 f (t)在t =0 处是连续的，由于δ(t) 仅仅t =0 时为非零值，其余时间均为零，则
  f (t) * δ(t) = f(0) * δ(0)
  由此可以有推论
  
  例题
  
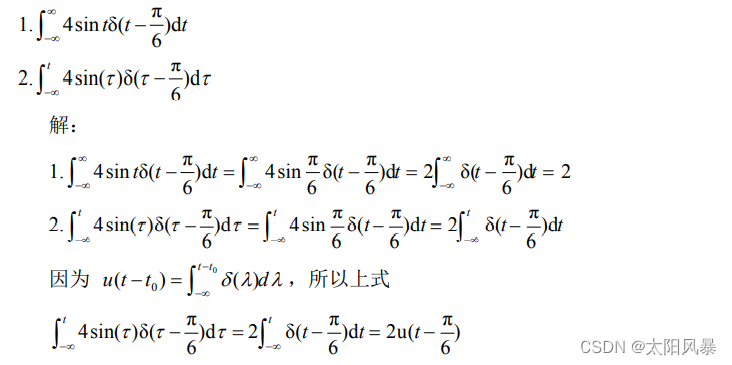
• 2、冲激偶信号与普通函数相乘
  f (t) * δ '(t) = f (0) * δ '(t) - f '(0) * δ(t)
  在通过定义的积分表达式推广后，有下面有用结论
  
• 3、尺度特性
  冲激信号的n 阶导数用 δ⁽ⁿ⁾(t 表示，其尺度特性可表示为：
  
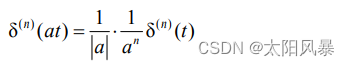
  这个公式就是万能公式。可以由此推出其他的结论
  
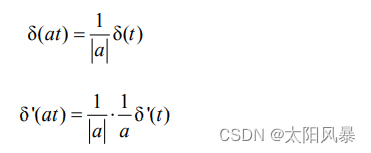
• 4、奇偶特性
  冲激函数具有偶函数特性，而冲激偶则具有奇函数特性
  当a = 1 时有
  
  当 n= 0 时
  

三、系统的特性及分类

系统的基本作用是将输入信号（也称为激励）经过传输、变换或处理后，在系统的输出端得到满足要求的输出信号（也称为响应）。这一过程可表示为系统的描述我们可以用下图来描述

y(●) 表示系统在激励 f (●)单独作用时产生的响应。信号变量用圆点标记，代表连续时间变量 t 或离散序号变量n。
根据系统输入、输出的情况，通常将只有单个输入信号和单个输出信号的系统称为单输入单输出系统；将有多个输入信号和多个输出信号的系统称为多输入多输出系统。

1. 系统的初始状态

在观察和分析系统时，总会有一个观察和分析的时间起始点，我们将它称为初始观察时刻 t₀ （或简称初始时刻 t₀ ）。它表示以 t₀ 时刻为界，我们只关心系统在 t > t₀ 时的输出，而对 t₀ 时刻以前系统的输出不感兴趣。以 t₀ 时刻为界，可以将输入信号分成历史输入 f₁ (t) 和当前输入 f₂(t)

• f (t)=f₁(t)+f₂(t), -∞ < t < +∞
  

在实际系统中会存在函数值在t=0 处可能发生跳变或出现冲激信号。就需要使需要用x(0^- ) 和 + x(0⁺ ) 分别表示观察起始点前一瞬间 t=0^- 和后一瞬间 t=0⁺ 的状态，分别称为 0^- 初始状态和 0⁺ 初始状态。0^- 时刻的状态反映了历史输入信号对系统作用的效果，0⁺ 时刻的状态则反映了历史输入信号和t=0 时刻输入信号共同作用于系统的效果。系统在t = 0时响应 y(t) 是由历史输入信号和当前输入共同决定的，而 0^- 初始状态 - x(0^- ) 反映了历史输入信号对系统的全部作用效果，所以也可以将响应 y(t) 看成是当前输入 f (t)和 - 0 初始状态 - x(0 ) 共同决定的。

• 系统的响应仅由当前输入信号决定，我们称这样的响应为系统的零状态响应
• 输出仅由 - 0 初始状态确定，我们称这样的响应为系统的零输入响应
• 零状态响应 + 零输入响应 = 全响应

2. 线性特性

线性特性需要两个，一个是齐次性、一个是可加性

• 齐次性
  当激励乘上一个任意的常数（包括复常数），如果系统的响应也将相应地乘上一个相同的常数
  f (●) → y(●) ，则 af (●) → ay(●)

• 叠加性或可加性
  如果任意两个激励共同作用时，系统的响应等于每个激励单独作用时所产生的响应之和
  f (●) → y (●) ，f (●) → y (●) 有
  {f₁(●), f₂(●)} → y₁(●)+ y₂(●) {f₁(●), f₂(●)} 表示两个激励同时作用于系统

• 齐次可加性
  如果一个系统既有齐次性又有可加性，就称该系统具有线性特性
  f (●) → y (●) ，f (●) → y (●) 有
  {a₁f₁(●), a₂f₂(●)} → a₁y₁(●)+ a₂y₂(●)

3. 时不变特性

参数不随时间变化的系统，称为时不变系统或定常系统，否则称为时变系统。
f (●) → y_f (●)
对连续系统有
f (t - t_d) → y_f(t - t_d)
对离散系统
f (k- k_d) → y_f(k - k_d)

例题

图像

实际的系统设计和分析中最常用的系统类型为 线性时不变系统。
如果一个系统既是线性的，也是时不变的，那么称这个系统为线性时不变（LinearTime Invariant）系统，简称 LTI 系统。

4. 因果特性

这个很好判断，如果任意时刻 t₁ 时输入 f (t₁)的响应 y(t₁) 都不依赖于 t > t₁ 时 f (t)的值，则称该系统是因果的或非超前的。这样，在因果系统里，不可能在输入加入系统前而获得输出（假设系统是零状态的）。 如果系统不是因果的，就称为非因果的或超前的。

例题

总结：

• 时间是因果信号判别的重要指标，不能响应的时间不能超过信号的结果

像阶跃信号就是典型的因果信号

5. 稳定性

一个系统，如果它对任何有界的激励 f (●) 所产生的零状态响应 y_f(●)  亦为有界的，就称该系统为有界输入/有界输出（Bound-input/Bound-output）稳定，简称BIBO 稳定，有时也称系统是零状态稳定的。例如电路系统等，都是稳定系统，因为不可能存在输出无限增大的情况。例如一个电子扩音器，可以实现对声音的放大，但这个放大不能是无限的，即当把人的声音看做输入（显然这个输入是有限的），则扩音器的声音就是系统的输出，这个输出也是有限的，所以是一个稳定系统。

总结：

• 有界输入 对应 有界输出 则稳定

参考上节内容：

• 信号与系统的描述-上节