[学习笔记]PageRank算法

news2024/10/7 6:51:12

参考资料：改变世界的谷歌PageRank算法

pagerank算法用于计算节点重要度

思想

如果网页被更多的入度(被引用)，则网页更重要。
被重要网站引用比被普通网站引用更加凸显重要性。
所以考虑一个网站是否重要，需要看引用它的网站是否重要，这就成了一个递归的问题。

理解pagerank的五个角度

迭代求解线性方程组

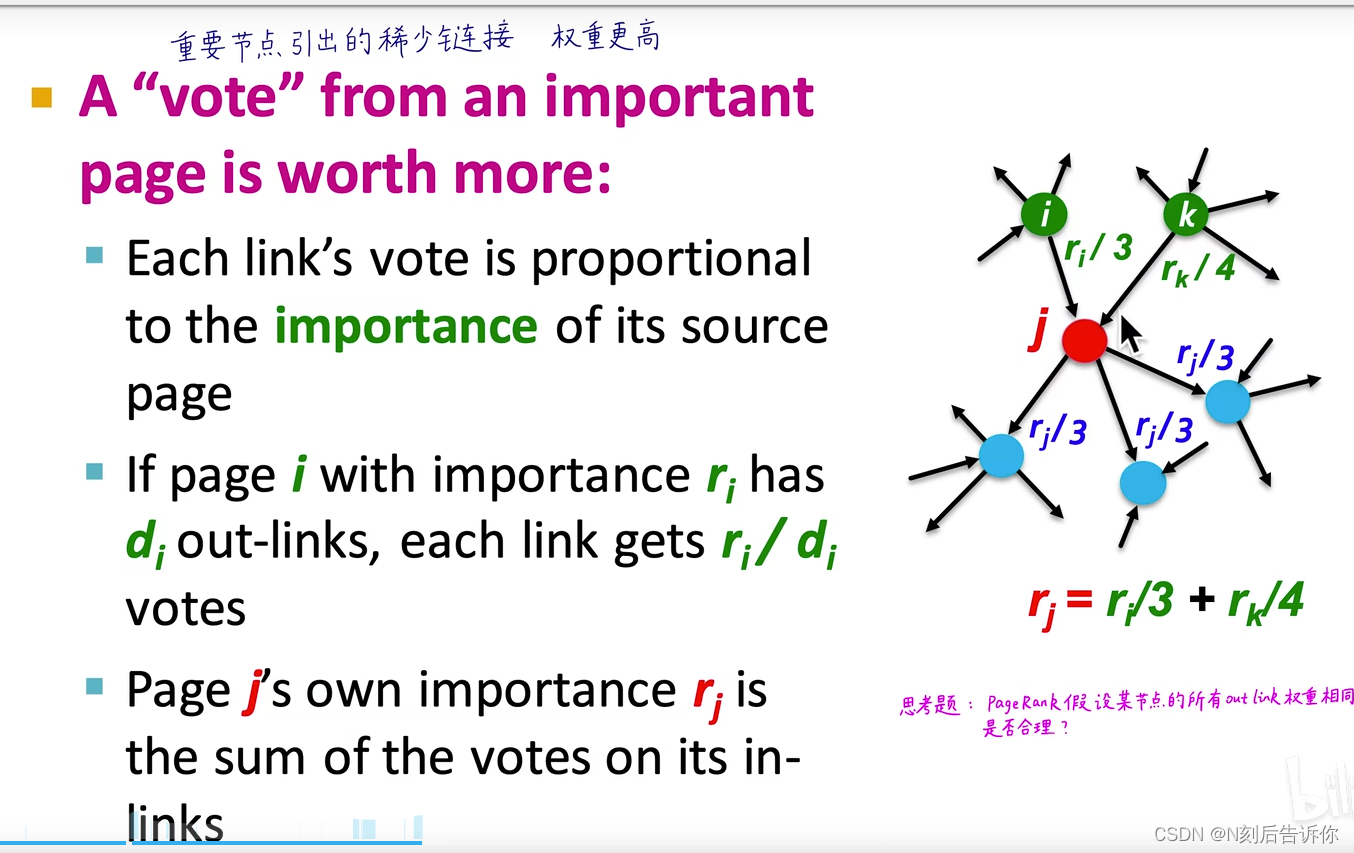
在这里插入图片描述

例子

在这里插入图片描述

这里看上去有三个方程，三个未知数，其实只有2个方程。
虽然高斯消元可以求解，但是可扩展性较差。
节点j的rank值 r j r_j rj​是考虑所有到 j j j的节点的rank值，各自除以它的出度，再求和。

迭代求解

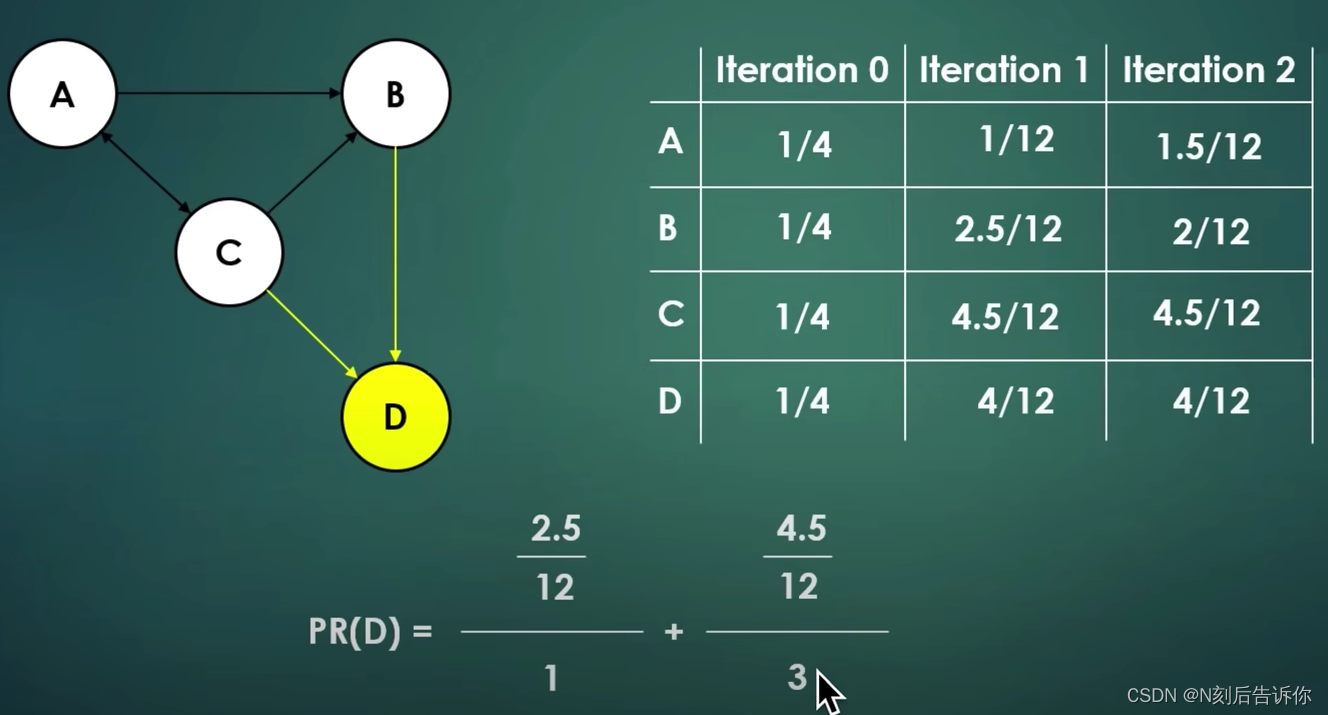
在这里插入图片描述

迭代左乘M矩阵

迭代的过程用矩阵表示：(左边的矩阵的i行j列 A i j 有非零值 A_{ij}有非零值 Aij​有非零值表示存在第j个节点到第i个节点的有向边)
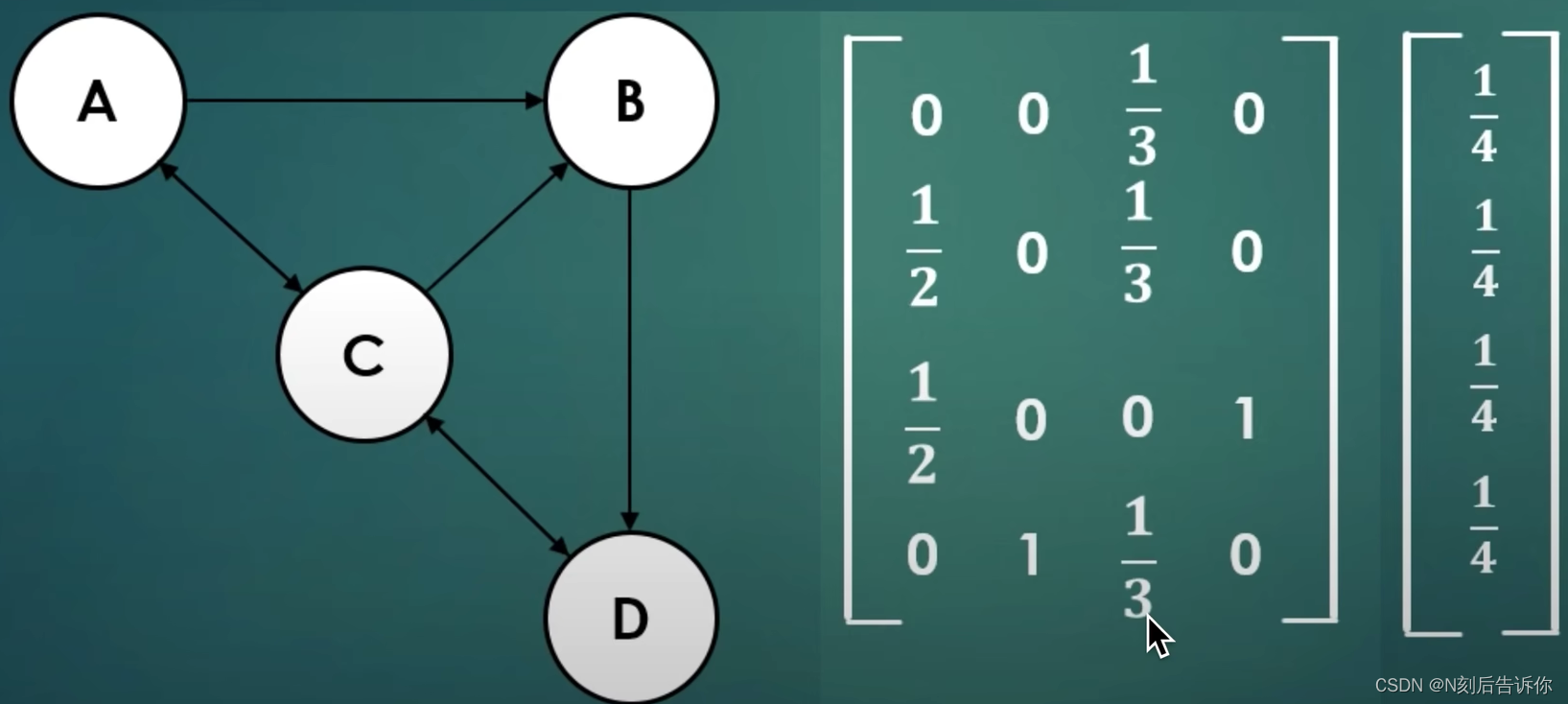
在这里插入图片描述

左边的矩阵称为列概率矩阵(列转移矩阵/列替代矩阵，column stochastic matrix)
右边的向量叫pagerank向量
在这里插入图片描述

矩阵的特征向量

迭代公式：
r = M ⋅ r r=M \cdot r r=M⋅r其实可以看作是
1 ⋅ r = M ⋅ r 1 \cdot r=M \cdot r 1⋅r=M⋅r
从这个角度看，pagerank向量就是M矩阵的特征值为1的特征向量。
在这里插入图片描述

对于Column Stochastic矩阵，由Perreon-Frobenius定理，最大的特征值就是1，且存在唯一的主特征向量(特征值1对应的特征向量)，向量所有元素求和为1。
通过幂迭代的方式，可以快速求解pagerank向量。

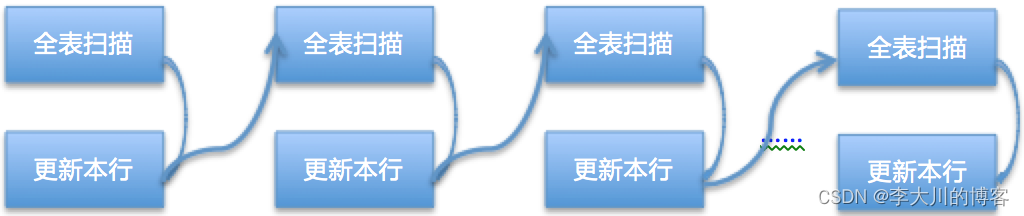
随机游走

随机游走->计数求和->归一化为概率，得到的就是pagerank向量。
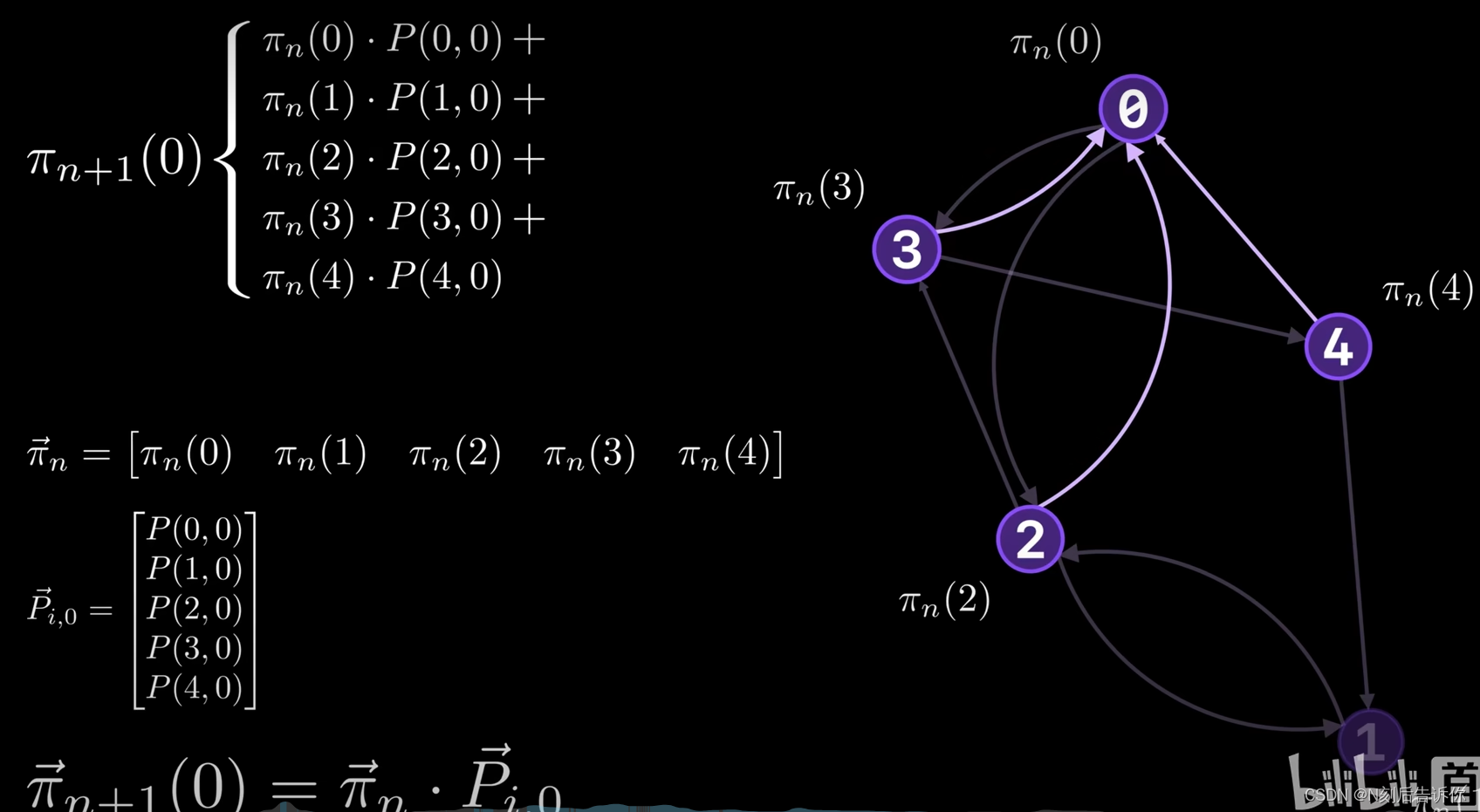
在这里插入图片描述
在这里插入图片描述

马尔科夫链

在这里插入图片描述
在这里插入图片描述

求解pagerank

在这里插入图片描述
在这里插入图片描述

收敛性分析

在这里插入图片描述

1. 是否收敛-收敛，收敛到同一个结果

Ergodic Theorem

根据Ergodic Theorem，对于不可约(irreducible)和非周期(aperiodic)的马尔可夫链：
1.存在一个唯一的稳定的马尔科夫分布
2.并且所有初始分布收敛到同一个分布

可约(reducible)马尔可夫链和不可约马尔可夫链

可约是存在孤立的状态
不可约是所有状态都可达
在这里插入图片描述

周期马尔可夫链和非周期马尔可夫链

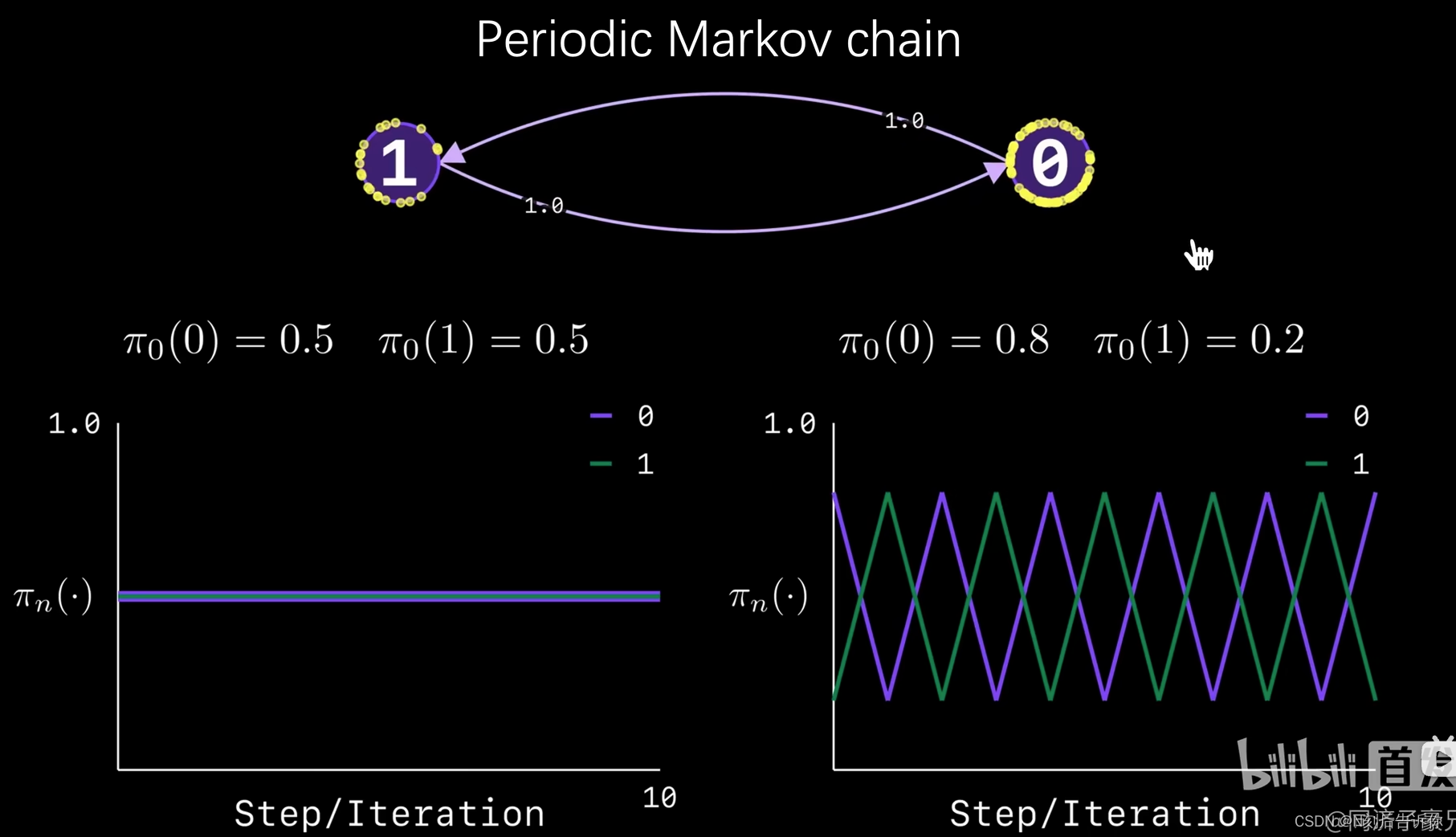
在这里插入图片描述

2.结果是不是代表重要度-两类问题

Spider trap问题

所有的出度边都在group里面，导致这个group吸收了所有的重要度
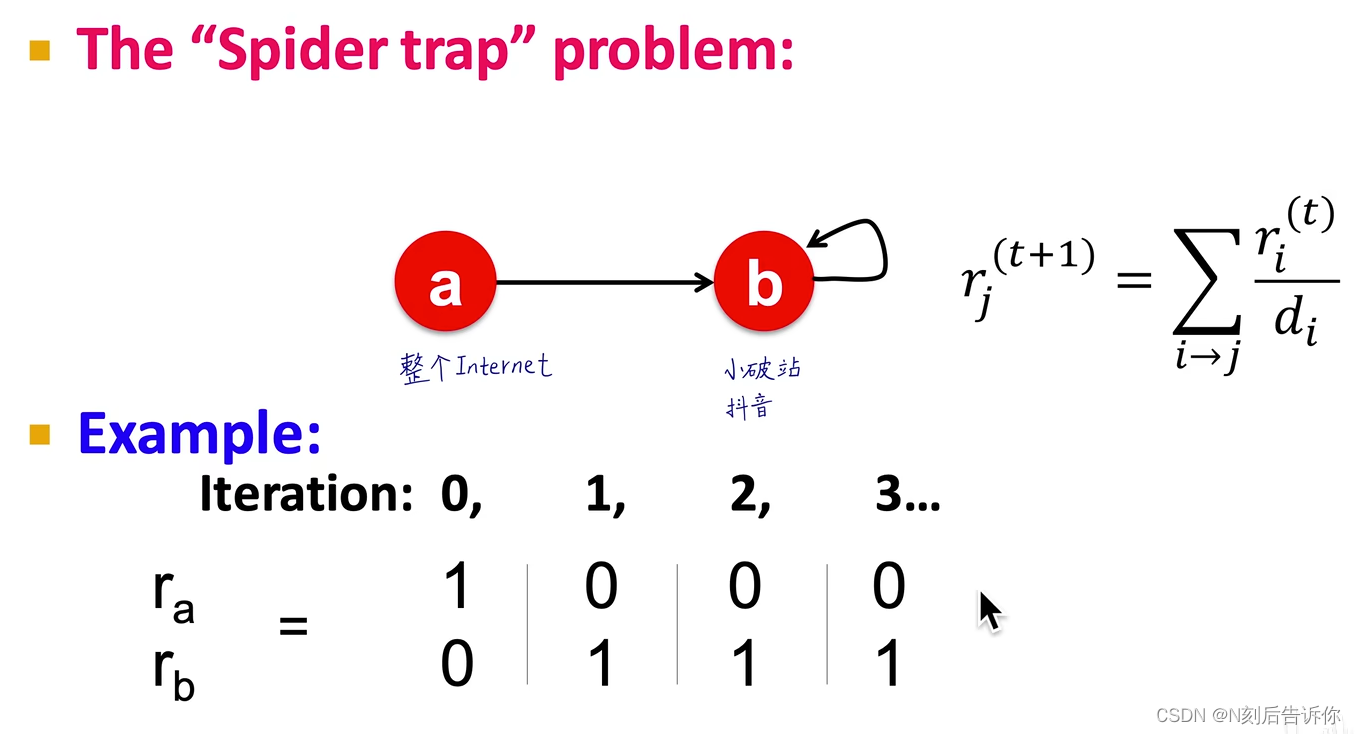
在这里插入图片描述

dead end问题

没有出度，重要度最终为0
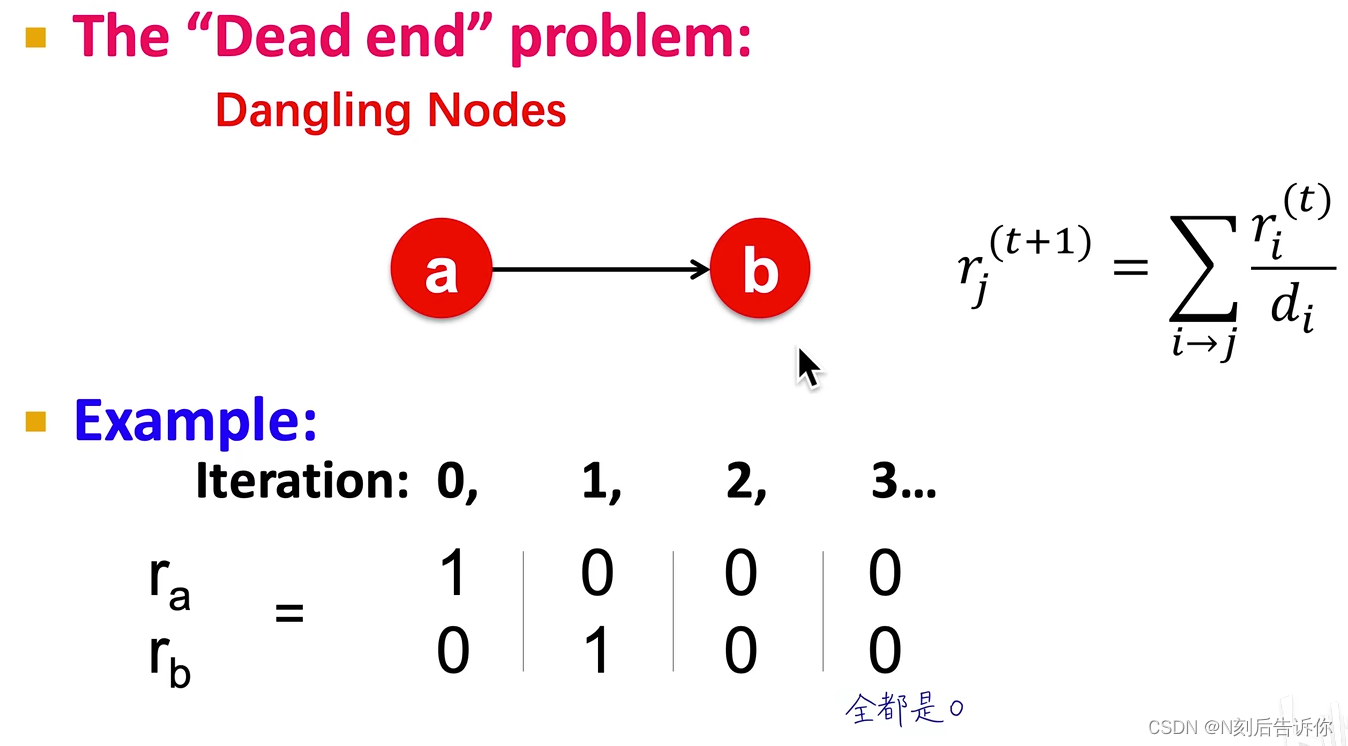
在这里插入图片描述
对于这两种情况，即使收敛了，也不是合理的网络重要度。

例子

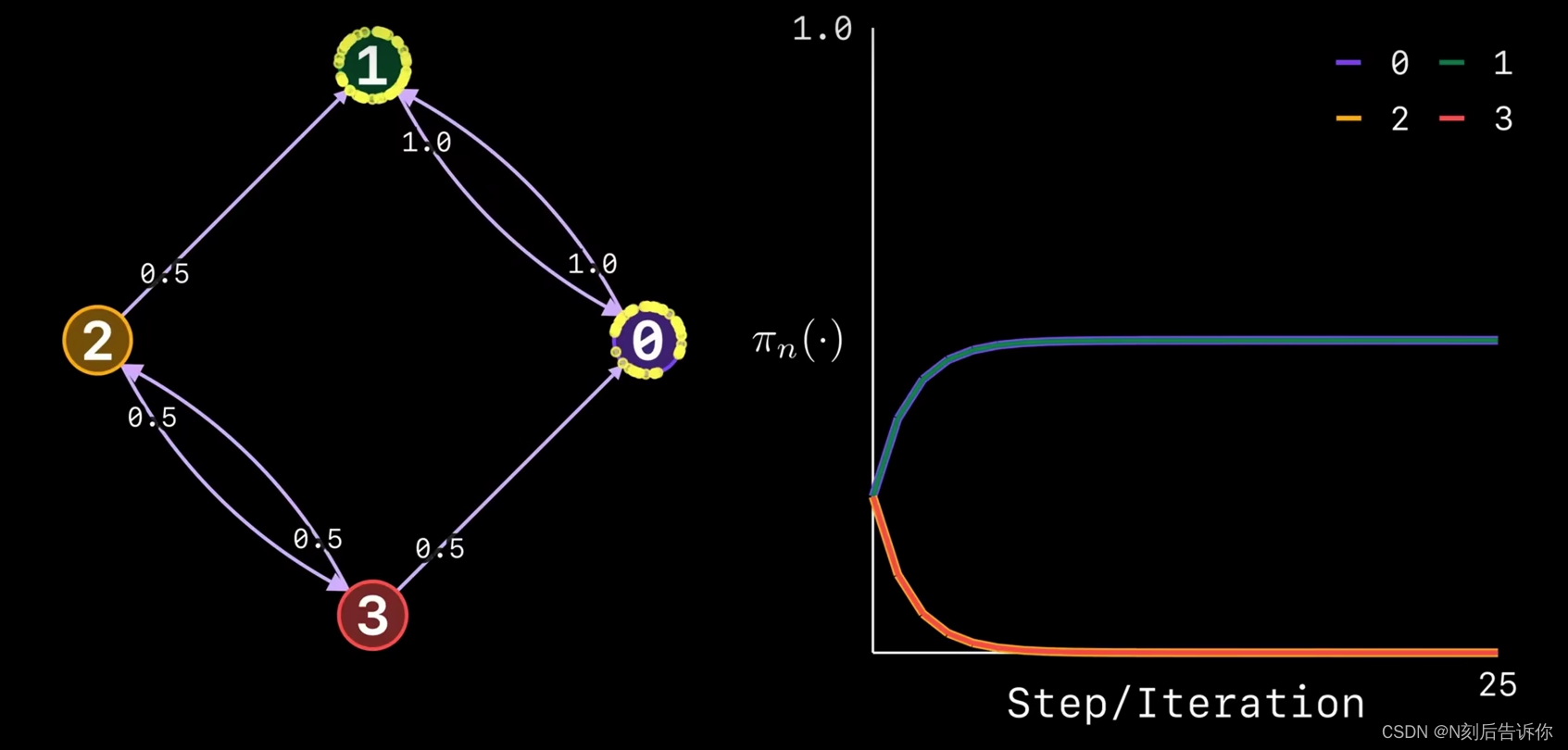
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

解决办法

spider trap问题的解决办法

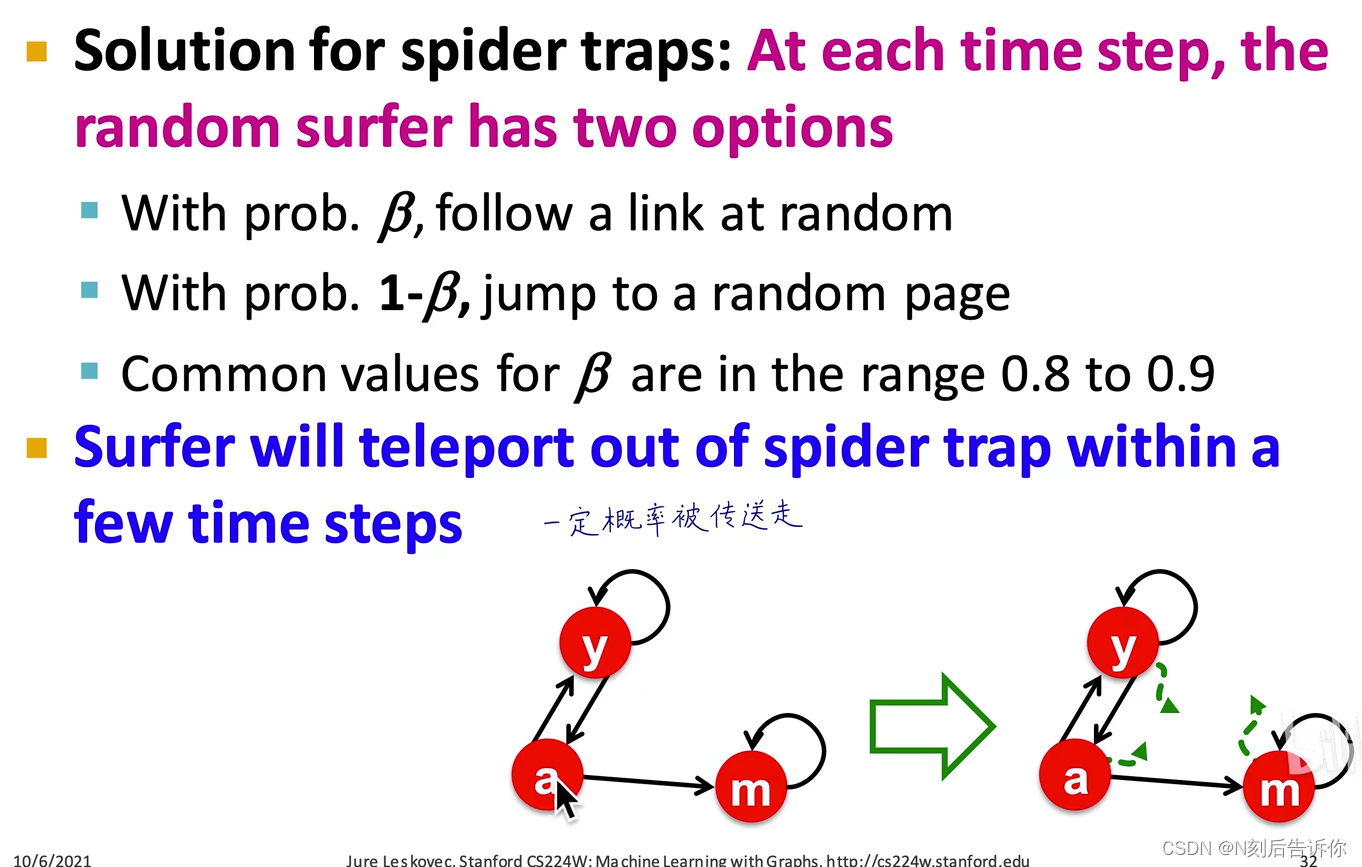
在这里插入图片描述

dead end的解决办法

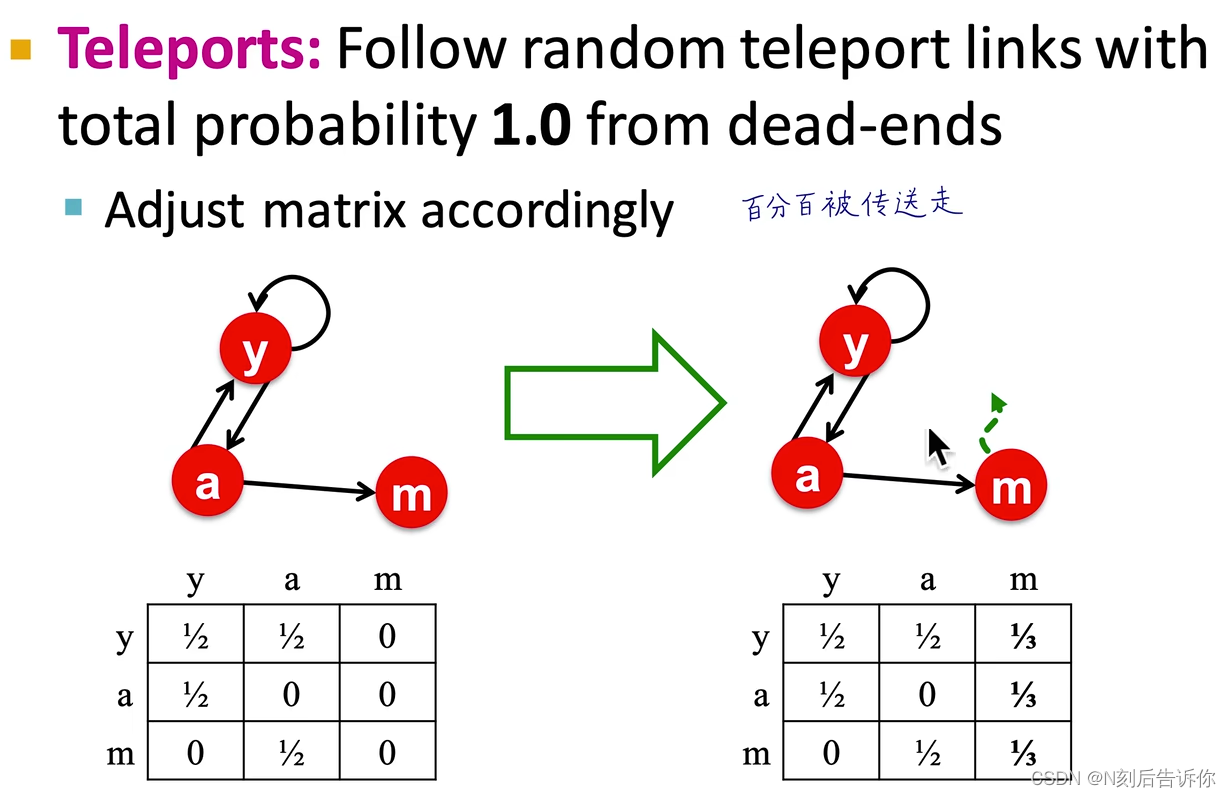
在这里插入图片描述

最终解决办法

在这里插入图片描述
在这里插入图片描述

pagerank的升级-mapreduce的工作

在这里插入图片描述

pagerank算法用于计算节点相似度-用于推荐系统

给定：一个bipartite graph用于表示用户和商品的交互
目标：寻找与指定节点最相似的节点
假设：被同一个用户访问过的节点，更可能是相似的

pagerank，随机游走视角的启发

pagerank的一种解释是：随机游走，并有概率随机传送到网络中的任意一个节点，继续游走
Topic-Specific PageRank(也称为personalized pagerank)：随机游走，并有传送到指定的一些节点，继续游走
random walks with restarts：随机游走，并有传送到指定的一个节点，继续游走

随机游走访问次数-相似性的度量

给定一个节点集query_nodes，模拟一个随机游走：

  • 记录访问次数
  • 在概率 α \alpha α下，在query_nodes中重启walk
  • 有高访问次数的节点则和query_nodes中的点有更高的相似性

伪代码

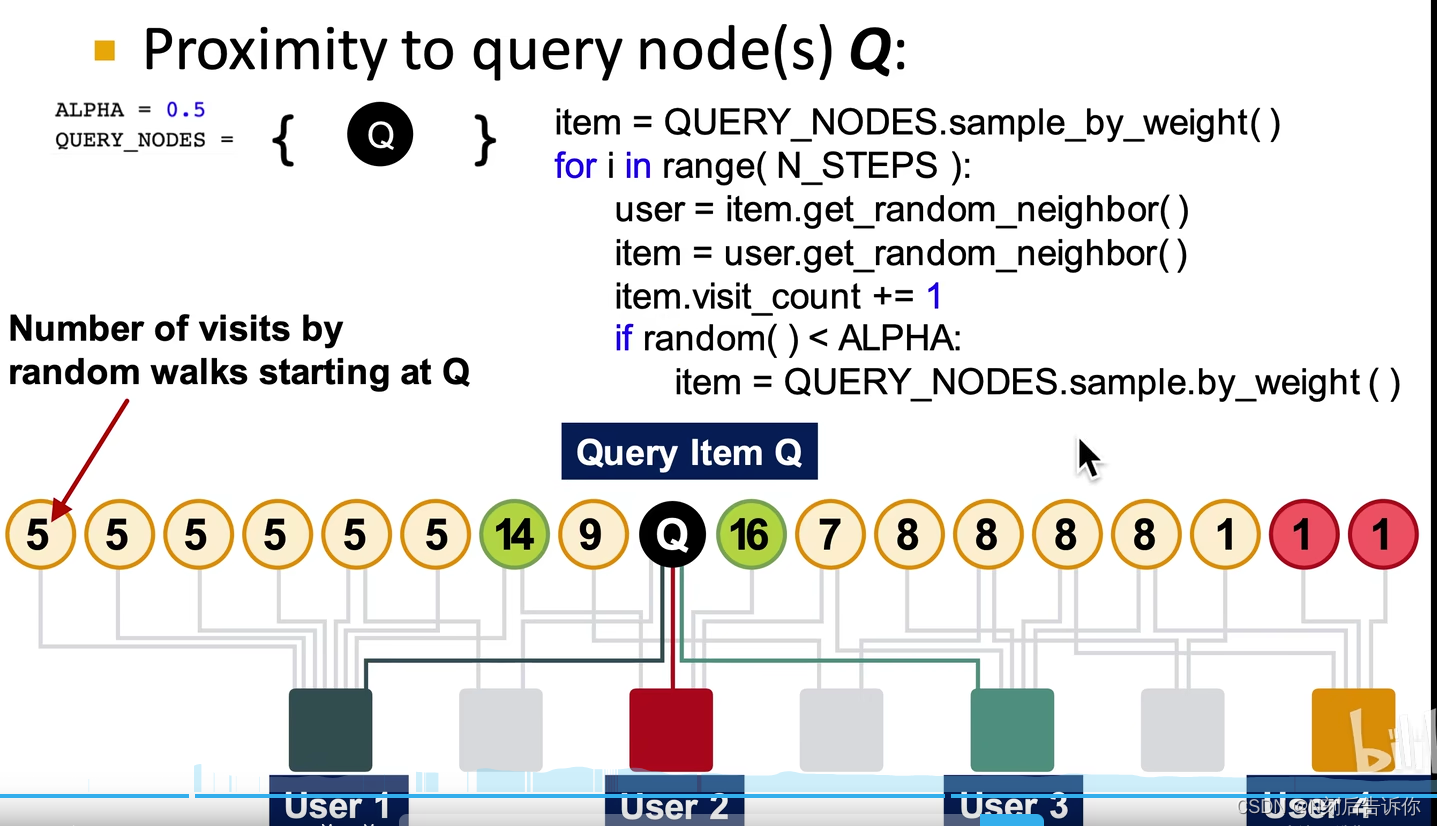
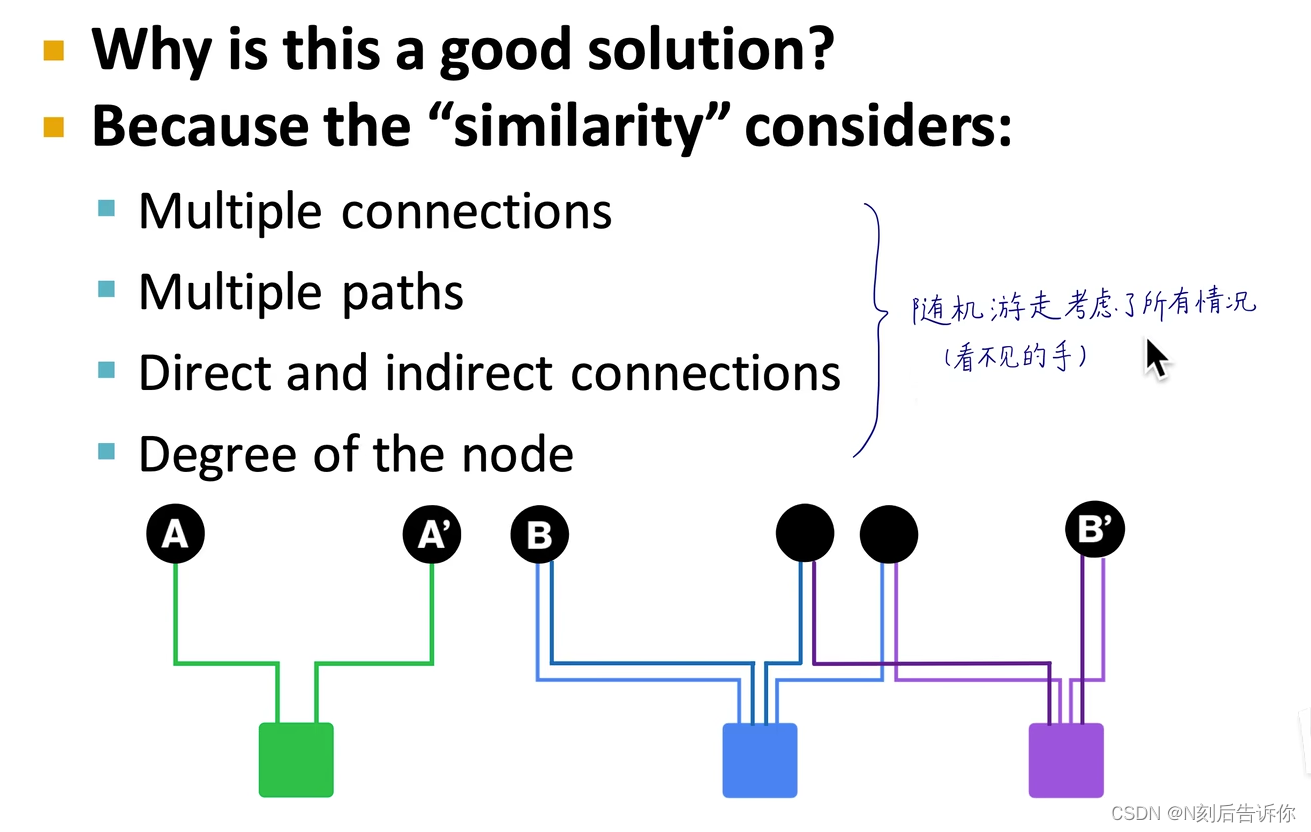
在这里插入图片描述

优点

在这里插入图片描述

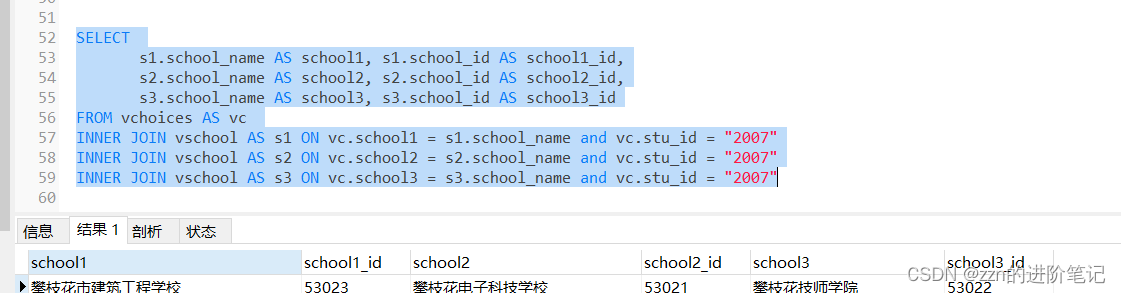
代码实战

参考资料：https://www.bilibili.com/video/BV1Wg411H7Ep/?p=16&spm_id_from=pageDriver

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1001750.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Mysql binlog的三种模式statement,row,mixed详解，以及无主键造成复制延时的测试

Mysql binlog的三种模式statement,row,mixed详解，以及无主键造成复制延时的测试

2.1 Statement 模式的概念 Statement 是基于语句的复制模式。 Statement 模式将数据库中执行的修改操作记录为 SQL 语句，再从数据库上执行相同的 SQL 语句来实现数据同步。 2.2 Statement 模式的优点 Statement 模式的优点是简单明了，易于理解和实现。…
阅读更多...
工作不好找，普通打工人如何破局

工作不好找，普通打工人如何破局

大家好，我是苍何，我的一位阿里朋友被裁后，找工作找了一个月都没结果，很多到最后一面被pass了，不由得做一下感慨，即使是大厂背景又如何，面对经济环境和大环境市场，每个人都不容易。 …
阅读更多...
关于一个left join的易错点

关于一个left join的易错点

很多人在学习mysql的时候应该都出现过很多问题，特别是连接方面的问题应该最多，希望这篇文章帮助到正在找bug的你 Java报错数据返回数量出现错误 遇到这种问题一定要看日志 很明显通过left join查询除了两条数据并且为空 马上思考错误的原因，…
阅读更多...
【playwright】访问不同链接方法

【playwright】访问不同链接方法

every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 访问不同页面方法方法比较 browser.new_page() page context.new_page() 1. 访问不同url 1.1 方法一 browser.new_page() 打开多个浏览器&#xff0…
阅读更多...
JS如何判断一个变量是否为数组类型？

JS如何判断一个变量是否为数组类型？

聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 使用 Array.isArray() 方法⭐ 使用 instanceof 操作符⭐ 使用 Object.prototype.toString.call() 方法⭐ 使用 Array.from() 方法⭐ 使用 Array.prototype.isArray 属性（不推荐）⭐ 写在最后 ⭐ 专栏简介 前端入门之…
阅读更多...
人机融合的熵增定律

人机融合的熵增定律

在信息论中，熵增定律是指在信息传输或处理过程中，总的熵（即不确定性或信息的度量）通常会增加。然而，对于人机融合的情况，熵增定律并不是一个普适的定律，而是取决于具体情境和应用。 当人与机器进…
阅读更多...
uniapp-小程序登录授权框

uniapp-小程序登录授权框

微信官方文档 不弹出授权框原因 因为版本问题，目前的最新的版本是不支持 wx.getUserInfo 去主动弹出授权框 只能引导用户去点击 butten 去授权 解决方法 我的思路是参考了其他的微信微信小程序, 就是跳转到我的页面的时候 在钩子函数内去触发一个封装的模态框,状…
阅读更多...
STM32-HAL库07-软件SPI驱动0.96寸OLED

STM32-HAL库07-软件SPI驱动0.96寸OLED

STM32-HAL库07-软件SPI驱动0.96寸OLED 一、所用材料： STM32VGT6自制控制板 STM32CUBEMX（HAL库软件） MDK5 二、所学内容： 通过HAL库配置四个GPIO输出口，对其进行软件模拟SPI发送规则，进而驱动OLED进行数…
阅读更多...
VisualStudio Code 支持C++11插件配置

VisualStudio Code 支持C++11插件配置

问题 Visual Studio Code中的插件: Code Runner 支持运行C、C、Java、JS、PHP、Python等多种语言。 但是它不支持C11特性的一些使用，比如类似错误： binarySearch.cpp:26:17: error: non-aggregate type ‘vector’ cannot be initialized with an ini…
阅读更多...
C++(day4)

C++(day4)

思维导图 封装Mystring #include <iostream> #include<cstring>using namespace std;class Mystring{ public://无参构造函数Mystring():size(10){strnew char[size];strcpy(str,"");cout<<"无参构造函数"<<endl;}//有参构造函数…
阅读更多...
前端内存泄漏和溢出的情况以及解决办法

前端内存泄漏和溢出的情况以及解决办法

写在前面&#xff1a; 在平时写代码时&#xff0c;内存泄漏的情况会时有发生&#xff0c;虽然js有内存回收机制&#xff0c;但在平时编程中还是需要注意避免内存泄漏的情况&#xff1b;前几天做移动端时遇到一个内存泄漏造成移动端页面卡顿的问题&#xff0c;所以想总结下前端…
阅读更多...
GO语言网络编程（并发编程）Channel

GO语言网络编程（并发编程）Channel

GO语言网络编程&#xff08;并发编程&#xff09;Channel 1、Channel 1.1.1 Channel 单纯地将函数并发执行是没有意义的。函数与函数间需要交换数据才能体现并发执行函数的意义。 虽然可以使用共享内存进行数据交换&#xff0c;但是共享内存在不同的goroutine中容易发生竞态…
阅读更多...
Linux Debian12使用git将本地项目打标签、创建分支和分支合并到master再上传到码云(gitee)远程仓库

Linux Debian12使用git将本地项目打标签、创建分支和分支合并到master再上传到码云(gitee)远程仓库

一、git创建分支并克隆指定分支到本地 gitee官网&#xff1a;https://gitee.com/ 登录上gitee账号,我这用test仓库作测试。新建分支名称为develop&#xff0c;分支起点选择master&#xff0c;创建即可&#xff0c;如下图所示&#xff1a; 使用git管理代码版本时&#xff0…
阅读更多...
SpringBoot 中的事务管理讲解

SpringBoot 中的事务管理讲解

Spring Boot 中的事务管理 在实际的开发中&#xff0c;事务是非常重要的一个概念。在 Spring Boot 中&#xff0c;我们可以使用事务管理器来管理事务。事务管理器可以确保一系列操作要么全部成功&#xff0c;要么全部失败&#xff0c;从而保证数据的一致性和完整性。在本文中&…
阅读更多...
音频驱动嘴型的视频数字人虚拟主播工具motionface replay使用教程

音频驱动嘴型的视频数字人虚拟主播工具motionface replay使用教程

音频驱动嘴型的视频数字人虚拟主播工具motionface replay使用教程 1&#xff1a;系统要求 软件运行支持32位/64位window 10/11系统&#xff0c;内存最低要求> 8Gb.无其他硬性要求。 1&#xff1a;下载安装 打开百度网盘链接下载&#xff1a; 链接&#xff1a;百度网盘 请输入…
阅读更多...
unityhub登录不上，登录界面刷新不出来, 或检测不到Unity

unityhub登录不上，登录界面刷新不出来, 或检测不到Unity

如果是登录界面白屏的话 或 检测不到Unity 可以尝试 1.关闭hub&#xff08;右下角也要退出&#xff0c;找不到的可以直接任务管理器退出&#xff09; 2.删除 %UserProfile%\AppData\Roaming 里面的 \UnityHub\Cache和\Unity\Caches 文件夹 C:\Users\Administrator\AppData\Ro…
阅读更多...
Linkstech多核并行仿真丨光伏发电系统模型及IEEE 39 bus模型多核并行实测

Linkstech多核并行仿真丨光伏发电系统模型及IEEE 39 bus模型多核并行实测

新能源场站和区域电网作为复杂且具有动态特性的大规模电力系统&#xff0c;需要实时仿真测试来验证其性能、稳定性和响应能力。在这种背景下&#xff0c;多核并行仿真运算显得尤为重要。多核并行仿真能够同时处理电力系统的复杂模型&#xff0c;加速仿真过程&#xff0c;实现接…
阅读更多...
C#自定义控件组件实现Chart图表（多Y轴，选择图例加粗，选择放大，缩放，点击查看信息等功能）

C#自定义控件组件实现Chart图表（多Y轴，选择图例加粗，选择放大，缩放，点击查看信息等功能）

先看看ECharts的效果 C# 工具箱里的Chart控件就不演示了，很多效果没办法做出来，做出来效果也很不理想。所以，需要自己去手动实现工具箱里的Chart没办法实现的效果； 先看看实现后的效果 绑定数据 点击图表 点击右侧图例加粗 选择放大 右键 点击缩小，恢复
阅读更多...
Docker Desktop使用宿主机Windows的配置文件持久化存储数据

Docker Desktop使用宿主机Windows的配置文件持久化存储数据

《微软官网Windows 上的 Docker 引擎帮助文档》 以Nginx为例 拉取Nginx镜像 docker pull nginx:1.23.1先启动Nginx&#xff0c;然后把Nginx的配置文件复制到Windows docker run --namenginx-1.23.1 -d -p 80:80 nginx:1.23.1把Nginx的配置文件复制到Windows 注意&#xff1…
阅读更多...
【算法训练-数组 四】【合并】：合并两个有序数组

【算法训练-数组 四】【合并】：合并两个有序数组

废话不多说&#xff0c;喊一句号子鼓励自己&#xff1a;程序员永不失业&#xff0c;程序员走向架构&#xff01;本篇Blog的主题是【数组合并】&#xff0c;使用【数组】这个基本的数据结构来实现&#xff0c;这个高频题的站点是&#xff1a;CodeTop&#xff0c;筛选条件为&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023