公众号:尤而小屋
作者:Peter
编辑:Peter
持续更新《Python深度学习》一书的精华内容,仅作为学习笔记分享。

本文是第4篇:基于Keras解决深度学习中的回归问题。
Keras内置数据集
回归问题中使用的是内置的波士顿房价数据集。在keras中有多个内置的数据集:
- 波士顿房价数据集
- CIFAR10数据集(包含10种类别的图片集)
- CIFAR100数据集(包含100种类别的图片集)
- MNIST数据集(手写数字图片集)
- Fashion-MNIST数据集(10种时尚类别的图片集)
- IMDB电影点评数据集
- 路透社新闻数据集
其中IMDB数据集在二分类问题中被使用过,路透社新闻数据集在多分类问题中被使用。
In [1]:
import numpy as np
np.random.seed(1234) # 设置随机种子
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore") # 忽略notebook中的警告
导入数据
In [2]:
from keras.datasets import boston_housing
(train_data,train_targets), (test_data, test_targets) = boston_housing.load_data()
查看数据的基本信息:
In [3]:
train_data[:3]
Out[3]:
array([[1.23247e+00, 0.00000e+00, 8.14000e+00, 0.00000e+00, 5.38000e-01,
6.14200e+00, 9.17000e+01, 3.97690e+00, 4.00000e+00, 3.07000e+02,
2.10000e+01, 3.96900e+02, 1.87200e+01],
[2.17700e-02, 8.25000e+01, 2.03000e+00, 0.00000e+00, 4.15000e-01,
7.61000e+00, 1.57000e+01, 6.27000e+00, 2.00000e+00, 3.48000e+02,
1.47000e+01, 3.95380e+02, 3.11000e+00],
[4.89822e+00, 0.00000e+00, 1.81000e+01, 0.00000e+00, 6.31000e-01,
4.97000e+00, 1.00000e+02, 1.33250e+00, 2.40000e+01, 6.66000e+02,
2.02000e+01, 3.75520e+02, 3.26000e+00]])
In [4]:
train_data.shape, test_data.shape
Out[4]:
((404, 13), (102, 13))
数据标准化
在机器学习中,对数据进行标准化是非常重要的,主要有以下原因:
- 消除量纲影响:不同特征的数值大小可能相差很大,例如重量和价格。如果这些特征之间具有很大的差异,那么某些特征的值可能会主导模型的训练过程,从而削弱其他特征的重要性。通过标准化,可以将所有特征的值缩放到相同的尺度上,消除量纲的影响。
- 加速收敛:在机器学习算法中,梯度下降是一种常用的优化算法。当数据存在较大的尺度差异时,梯度更新可能会变得非常慢,导致算法收敛速度变慢。通过标准化,可以减少尺度差异,从而加速梯度下降算法的收敛速度。
- 提高模型性能:标准化可以使数据分布更加均匀,避免出现极端值或离群点。这有助于提高模型的泛化能力和性能。 因此,对数据进行标准化是机器学习中一个重要的预处理步骤,可以提升模型的训练效果和预测性能。
首先求出训练集的均值和标准差,进行标准化;再使用训练集的均值和标准差对测试集进行标准化。
In [5]:
# 手动标准化
mean = train_data.mean(axis=0) # 均值
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
对测试集的标准化:
In [6]:
# 仍然使用训练集的mean std
test_data -= mean
test_data /= std
搭建网络
In [7]:
from keras import models, layers
In [8]:
def build_model():
model = models.Sequential()
# 输入层
model.add(layers.Dense(64,activation="relu",input_shape=(train_data.shape[1],)))
# 隐藏层
model.add(layers.Dense(64,activation="relu"))
# 输出层:回归问题预测一个值,最终只有一个单元
model.add(layers.Dense(1))
model.compile(optimizer="rmsprop", # 优化器
loss="mse", # 损失
metrics=["mae"]) # 评价指标
return model
k折交叉验证
本小节的部分代码和原文有不同:
In [9]:
k = 5 # k折
num_val_samples = (len(train_data)) // k
num_epochs = 500
all_mae = []
all_val_mae = []
all_loss = []
all_val_loss = []
for i in range(k):
print(f"第 {i+1} fold正在running")
# 准备验证集数据
valid_data = train_data[i*num_val_samples:(i+1)*num_val_samples]
valid_targets = train_targets[i*num_val_samples:(i+1)*num_val_samples]
# 准备训练集(除去验证集部分)
part_train_data = np.concatenate([
train_data[:i*num_val_samples], # 索引i之前和i+1之后,两部分合并起来成为训练集
train_data[(i+1)*num_val_samples:]
],axis=0)
part_train_targets = np.concatenate([
train_targets[:i*num_val_samples],
train_targets[(i+1)*num_val_samples:]
],axis=0)
# 模型训练
model = build_model()
history = model.fit(part_train_data,
part_train_targets,
epochs=num_epochs,
batch_size=1,
verbose=0, # 静默模式,不显示每个epochs的具体打印信息
validation_data=[valid_data,valid_targets])
history_dict = history.history
mae = history_dict["mae"] # 训练集的mae
val_mae = history_dict["val_mae"] # 训练集的mae
loss = history_dict["loss"]
val_loss = history_dict["val_loss"]
all_mae.append(mae)
all_val_mae.append(val_mae)
all_loss.append(loss)
all_val_loss.append(val_loss)
第 1 fold正在running
第 2 fold正在running
第 3 fold正在running
第 4 fold正在running
第 5 fold正在running
模型指标可视化
In [10]:
len(all_mae) # 5折
Out[10]:
5
In [11]:
# all_mae[0] # 第1折的全部信息
第1折有500个元素(epochs=500)
In [12]:
len(all_mae[0])
Out[12]:
500
计算每个指标的平均值:
In [13]:
mae_average = [np.mean([x[i] for x in all_mae]) for i in range(num_epochs)]
mae_val_average = [np.mean([x[i] for x in all_val_mae]) for i in range(num_epochs)]
loss_average = [np.mean([x[i] for x in all_loss]) for i in range(num_epochs)]
loss_val_average = [np.mean([x[i] for x in all_val_loss]) for i in range(num_epochs)]
LOSS
In [14]:
num_epochs
Out[14]:
500
In [15]:
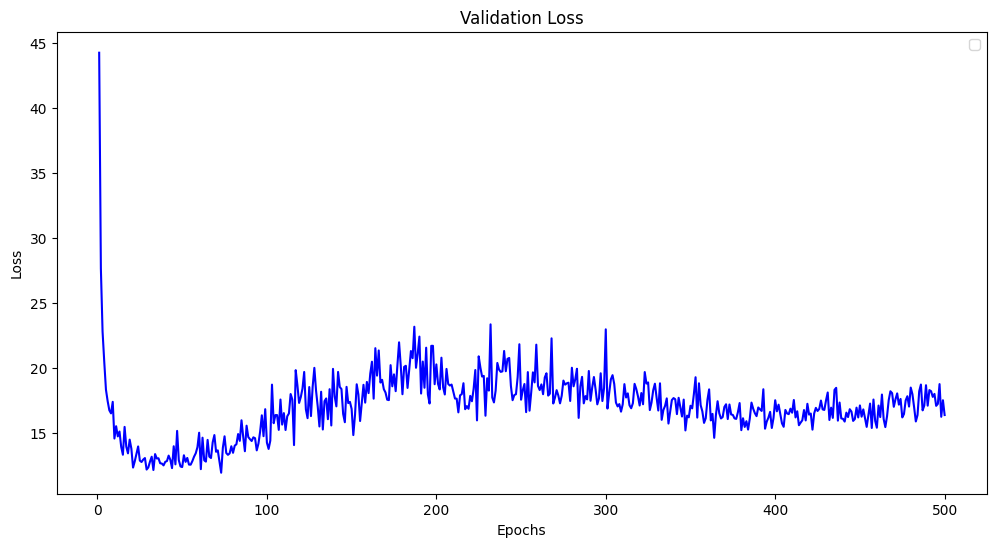
epochs = range(1, num_epochs+ 1) # 作为横轴
plt.figure(figsize=(12,6))
plt.plot(epochs, loss_val_average, "blue")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.title("Validation Loss")
plt.show()
基于plotly绘制图像:
In [16]:
import plotly_express as px
px.scatter(x=epochs,y=loss_val_average)

In [17]:
epochs = range(1, num_epochs+ 1) # 作为横轴
plt.figure(figsize=(12,6))
plt.plot(epochs, loss_average, "blue", label="Training Loss")
plt.plot(epochs, loss_val_average, "red", label="Validation Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.title("Training and Validation Loss")
plt.show()

MAE
In [18]:
epochs = range(1, num_epochs+1) # 作为横轴
plt.plot(epochs, mae_average, "blue", label="Training MAE")
plt.plot(epochs, mae_val_average, "red", label="Validation MAE")
plt.xlabel("Epochs")
plt.ylabel("MAE")
plt.legend()
plt.title("Training and Validation MAE")
plt.show()

模型优化
可以看到,在训练集或者验证集上,不管是损失Loss还是误差MAE,前面的10个数据点和其他点差异很大,属于异常值,考虑直接删除。
数据的平滑处理:将每个数据点替换为前面数据点的平均值,得到较为光滑的曲线。
In [19]:
def smooth(points, factor=0.9):
smooth_points = []
for point in points:
if smooth_points:
previous = smooth_points[-1]
smooth_points.append(previous * factor + point * (1 - factor)) # 前一个点 * 0.9 + 当前点 * 0.1
else: # 不存在元素则添加point点
smooth_points.append(point)
return smooth_points
排除前10个点后进行平滑处理:
In [20]:
smooth_mae = smooth(mae_average[10:])
smooth_mae_val = smooth(mae_val_average[10:])
smooth_loss = smooth(loss_average[10:])
smooth_loss_val = smooth(loss_val_average[10:])
新LOSS
In [21]:
epochs = range(1, len(smooth_mae)+ 1) # 作为横轴
plt.figure(figsize=(12,6))
plt.plot(epochs, smooth_loss, "blue", label="Training Loss")
plt.plot(epochs, smooth_loss_val, "red", label="Validation Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.title("Smoothed Training and Validation Loss")
plt.show()

# fig = px.scatter(x=epochs, y=smooth_mae)
fig = px.scatter(x=epochs, y=smooth_loss_val)
fig.show()

新MAE
In [23]:
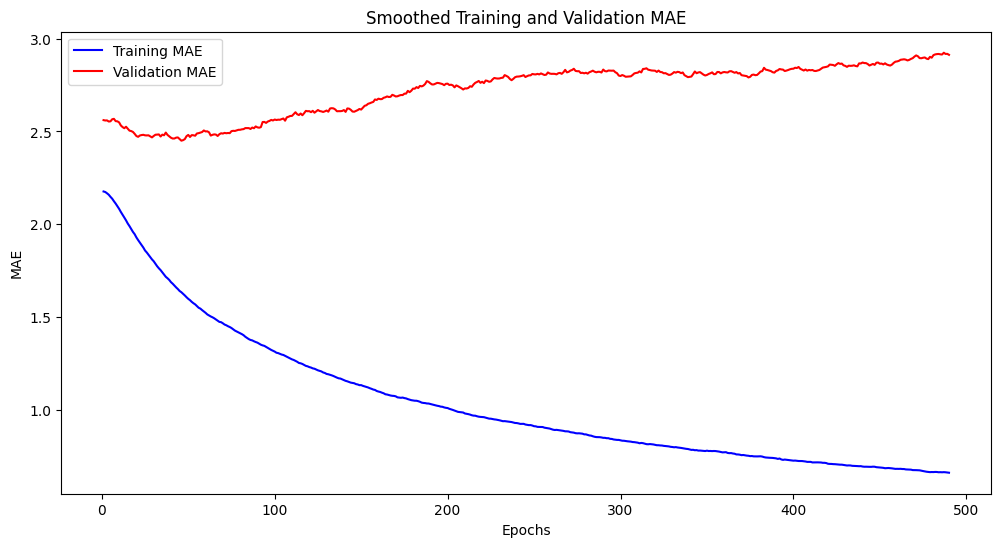
epochs = range(1, len(smooth_mae)+ 1) # 作为横轴
plt.figure(figsize=(12,6))
plt.plot(epochs, smooth_mae, "blue", label="Training MAE")
plt.plot(epochs, smooth_mae_val, "red", label="Validation MAE")
plt.xlabel("Epochs")
plt.ylabel("MAE")
plt.legend()
plt.title("Smoothed Training and Validation MAE")
plt.show()
# fig = px.scatter(x=epochs, y=smooth_mae)
fig = px.scatter(x=epochs, y=smooth_mae_val)
fig.show()
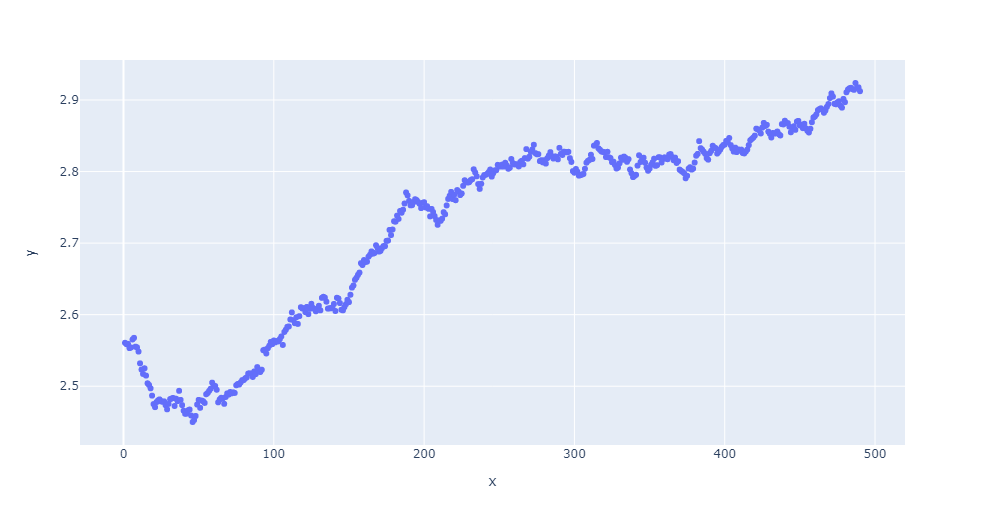
可以看到:在训练集上loss和mae随着轮次的进行,都在逐渐变小;但是在验证集上,并非如此,在50轮左右降到最低;