算法拾遗三十九SB树及跳表
- SB树
- SB树四种违规类型
- 总结
- SB树Code
- 跳表
SB树
SB树是基于搜索二叉树来的,也有左旋和右旋的操作,只是不同于AVL树,它也有它自己的一套平衡性方法。
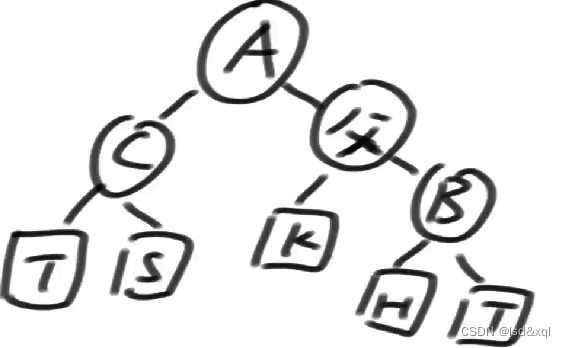
任何以叔叔节点为头的子树的节点个数不小于自己任何一个侄子树的节点个数。
如下图:
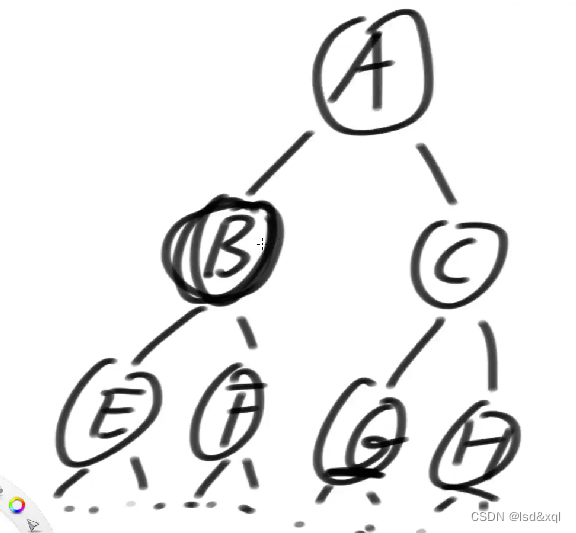
对于节点B是节点GH的叔叔,B整棵树的节点个数,不能比G或者H任何一个节点个数少,同理C整颗节点个数一定不能比E或者F这两棵树的节点个数少。
如果每个节点作为叔叔节点都能满足如上标准,那么称这棵树为Size Balance Tree。
得到:
AVL树维护的平衡因子是两颗子树的高度,而SB树则维护的是节点的size
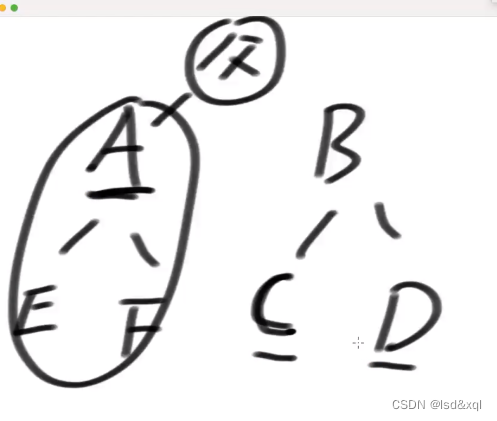
最悬殊的情况:
假设一棵树左树的节点比较少,右树的节点比较多,左树的A节点不能比右树的C节点以及D节点少,如果这棵树的右树是比较多的节点,也能满足左右两棵树不会特别悬殊,以此来达到高度收敛于O(logN)的效果
SB树四种违规类型
LL:
我左儿子的左边的节点个数,多余了我父儿子的节点个数
LR:
我左儿子的右孩子的节点个数,多余了我右孩子的节点个数
RL:
我左儿子的节点个数,小于右儿子的左孩子节点个数
RR:
我左儿子的节点个数,授予我右儿子的右孩子的节点个数
假设现在有个LL型违规:
假设进行一个m函数的调整,传入父节点,去做调整,然后返回一个父亲节点。
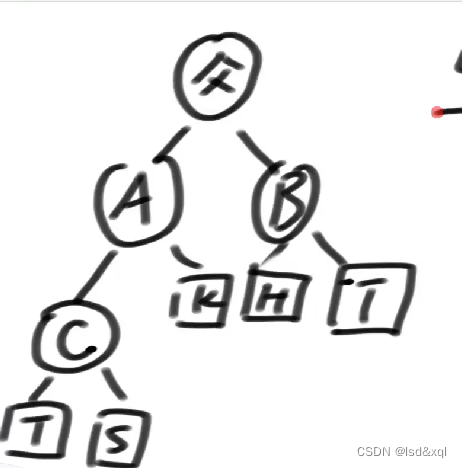
如上图所示,假设是AVL树进行右旋,得到如下所示:
但是SB树则需要进行进一步的调整,需要找到谁的孩子发生了变化:
A的孩子节点发生了变化,以及父节点的孩子也发生了变化。
此时需要递归的调用m(A)以及m(父),重复的查是否发生了违规。
AVL树是一个平衡性非常敏感的树,所以每次加一个节点以及删一个节点都会有一系列的调整,而SB树则是关注侄子节点的个数之间的关系,所以可能是很久才需要调整一次,没有AVL树那么敏感。
LL违规代码片段:
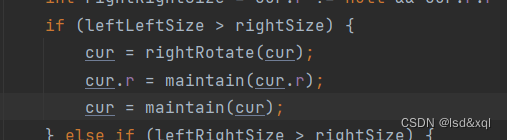
之所以都用返回值是为了防止在递归的过程中再次出现换头。
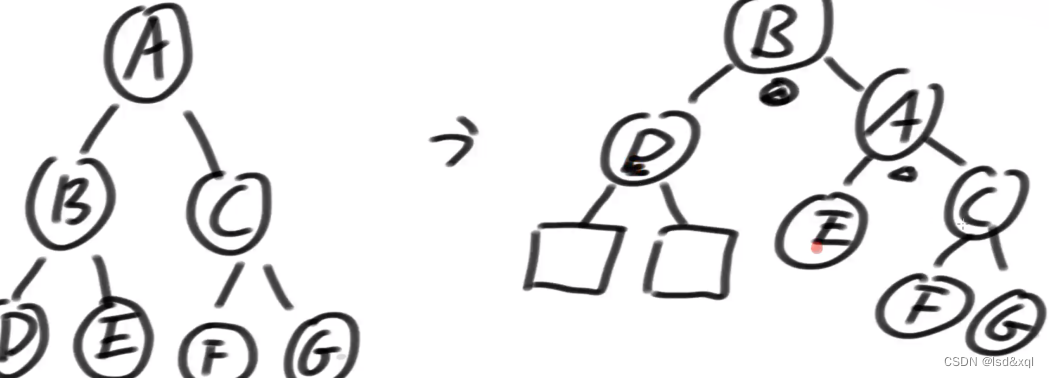
D现在面对的对手是E和C,在原树中D不以E做对手,以C做对手,D的节点比C多才会出现如上的右旋调整,现在D以E做对手了,可能出现违规(E可能把D干掉,可能需要调整),现在的C以E的两个孩子做对手,同时现在的E以F和G做对手也不知道它是否平衡,所以得去做递归。
总结
四种违规类型得调整和AVL树一样,不一样得地方就在于谁的孩子变了,则需要重新递归调用,SB树在删除得时候可以不用去做平衡性调整,在加入节点得过程中进行平衡性调整,因为递归是具有传递性的。
SB树Code
public static class SBTNode<K extends Comparable<K>, V> {
public K key;
public V value;
public SBTNode<K, V> l;
public SBTNode<K, V> r;
public int size; // 不同的key的数量
public SBTNode(K key, V value) {
this.key = key;
this.value = value;
size = 1;
}
}
public static class SizeBalancedTreeMap<K extends Comparable<K>, V> {
private SBTNode<K, V> root;
private SBTNode<K, V> rightRotate(SBTNode<K, V> cur) {
SBTNode<K, V> leftNode = cur.l;
cur.l = leftNode.r;
leftNode.r = cur;
//不同于AVL树换size
leftNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return leftNode;
}
private SBTNode<K, V> leftRotate(SBTNode<K, V> cur) {
SBTNode<K, V> rightNode = cur.r;
cur.r = rightNode.l;
rightNode.l = cur;
rightNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return rightNode;
}
private SBTNode<K, V> maintain(SBTNode<K, V> cur) {
if (cur == null) {
return null;
}
int leftSize = cur.l != null ? cur.l.size : 0;
int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
int rightSize = cur.r != null ? cur.r.size : 0;
int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
//LL违规,右旋
if (leftLeftSize > rightSize) {
cur = rightRotate(cur);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (leftRightSize > rightSize) {
//先左旋后右旋
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
//返回的新头部被cur的左孩子捕获
cur.l = maintain(cur.l);
//返回的新头部被cur的右孩子捕获
cur.r = maintain(cur.r);
//自己调整
cur = maintain(cur);
} else if (rightRightSize > leftSize) {
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur = maintain(cur);
} else if (rightLeftSize > leftSize) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
}
return cur;
}
private SBTNode<K, V> findLastIndex(K key) {
SBTNode<K, V> pre = root;
SBTNode<K, V> cur = root;
while (cur != null) {
pre = cur;
if (key.compareTo(cur.key) == 0) {
break;
} else if (key.compareTo(cur.key) < 0) {
cur = cur.l;
} else {
cur = cur.r;
}
}
return pre;
}
private SBTNode<K, V> findLastNoSmallIndex(K key) {
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.key) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.key) < 0) {
ans = cur;
cur = cur.l;
} else {
cur = cur.r;
}
}
return ans;
}
private SBTNode<K, V> findLastNoBigIndex(K key) {
SBTNode<K, V> ans = null;
SBTNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.key) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.key) < 0) {
cur = cur.l;
} else {
ans = cur;
cur = cur.r;
}
}
return ans;
}
// 现在,以cur为头的树上,新增,加(key, value)这样的记录
// 加完之后,会对cur做检查,该调整调整
// 返回,调整完之后,整棵树的新头部
private SBTNode<K, V> add(SBTNode<K, V> cur, K key, V value) {
if (cur == null) {
return new SBTNode<K, V>(key, value);
} else {
cur.size++;
//新加的key去左边或者右边
if (key.compareTo(cur.key) < 0) {
cur.l = add(cur.l, key, value);
} else {
cur.r = add(cur.r, key, value);
}
//cur自己调m传递下去
return maintain(cur);
}
}
// 在cur这棵树上,删掉key所代表的节点
// 返回cur这棵树的新头部
private SBTNode<K, V> delete(SBTNode<K, V> cur, K key) {
cur.size--;
if (key.compareTo(cur.key) > 0) {
cur.r = delete(cur.r, key);
} else if (key.compareTo(cur.key) < 0) {
cur.l = delete(cur.l, key);
} else { // 当前要删掉cur
if (cur.l == null && cur.r == null) {
// free cur memory -> C++
cur = null;
} else if (cur.l == null && cur.r != null) {
// free cur memory -> C++
cur = cur.r;
} else if (cur.l != null && cur.r == null) {
// free cur memory -> C++
cur = cur.l;
} else { // 有左有右
SBTNode<K, V> pre = null;
SBTNode<K, V> des = cur.r;
des.size--;
while (des.l != null) {
pre = des;
des = des.l;
des.size--;
}
if (pre != null) {
pre.l = des.r;
des.r = cur.r;
}
des.l = cur.l;
des.size = des.l.size + (des.r == null ? 0 : des.r.size) + 1;
// free cur memory -> C++
cur = des;
}
}
// cur = maintain(cur); 可以删掉,删除的时候不调整平衡性
return cur;
}
private SBTNode<K, V> getIndex(SBTNode<K, V> cur, int kth) {
if (kth == (cur.l != null ? cur.l.size : 0) + 1) {
return cur;
} else if (kth <= (cur.l != null ? cur.l.size : 0)) {
return getIndex(cur.l, kth);
} else {
return getIndex(cur.r, kth - (cur.l != null ? cur.l.size : 0) - 1);
}
}
public int size() {
return root == null ? 0 : root.size;
}
public boolean containsKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
return lastNode != null && key.compareTo(lastNode.key) == 0 ? true : false;
}
// (key,value) put -> 有序表 新增、改value
public void put(K key, V value) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.key) == 0) {
lastNode.value = value;
} else {
root = add(root, key, value);
}
}
public void remove(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
if (containsKey(key)) {
root = delete(root, key);
}
}
public K getIndexKey(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).key;
}
public V getIndexValue(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).value;
}
public V get(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.key) == 0) {
return lastNode.value;
} else {
return null;
}
}
public K firstKey() {
if (root == null) {
return null;
}
SBTNode<K, V> cur = root;
while (cur.l != null) {
cur = cur.l;
}
return cur.key;
}
public K lastKey() {
if (root == null) {
return null;
}
SBTNode<K, V> cur = root;
while (cur.r != null) {
cur = cur.r;
}
return cur.key;
}
public K floorKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNoBigNode = findLastNoBigIndex(key);
return lastNoBigNode == null ? null : lastNoBigNode.key;
}
public K ceilingKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);
return lastNoSmallNode == null ? null : lastNoSmallNode.key;
}
}
// for test
public static void printAll(SBTNode<String, Integer> head) {
System.out.println("Binary Tree:");
printInOrder(head, 0, "H", 17);
System.out.println();
}
// for test
public static void printInOrder(SBTNode<String, Integer> head, int height, String to, int len) {
if (head == null) {
return;
}
printInOrder(head.r, height + 1, "v", len);
String val = to + "(" + head.key + "," + head.value + ")" + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.l, height + 1, "^", len);
}
// for test
public static String getSpace(int num) {
String space = " ";
StringBuffer buf = new StringBuffer("");
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
public static void main(String[] args) {
SizeBalancedTreeMap<String, Integer> sbt = new SizeBalancedTreeMap<String, Integer>();
sbt.put("d", 4);
sbt.put("c", 3);
sbt.put("a", 1);
sbt.put("b", 2);
// sbt.put("e", 5);
sbt.put("g", 7);
sbt.put("f", 6);
sbt.put("h", 8);
sbt.put("i", 9);
sbt.put("a", 111);
System.out.println(sbt.get("a"));
sbt.put("a", 1);
System.out.println(sbt.get("a"));
for (int i = 0; i < sbt.size(); i++) {
System.out.println(sbt.getIndexKey(i) + " , " + sbt.getIndexValue(i));
}
printAll(sbt.root);
System.out.println(sbt.firstKey());
System.out.println(sbt.lastKey());
System.out.println(sbt.floorKey("g"));
System.out.println(sbt.ceilingKey("g"));
System.out.println(sbt.floorKey("e"));
System.out.println(sbt.ceilingKey("e"));
System.out.println(sbt.floorKey(""));
System.out.println(sbt.ceilingKey(""));
System.out.println(sbt.floorKey("j"));
System.out.println(sbt.ceilingKey("j"));
sbt.remove("d");
printAll(sbt.root);
sbt.remove("f");
printAll(sbt.root);
}
跳表
先看流程:
在有序表最顶层上面放一个最小值,可以认为是系统最小,然后进来一个值,经过计算得到一个层数信息。
如下图先进来一个3,它的层数是2,那么就造两层树,让第二层指向3,后面进来一个4,计算它的层数为3,那么则新建层数让第三层指向4,剩下的节点去连空
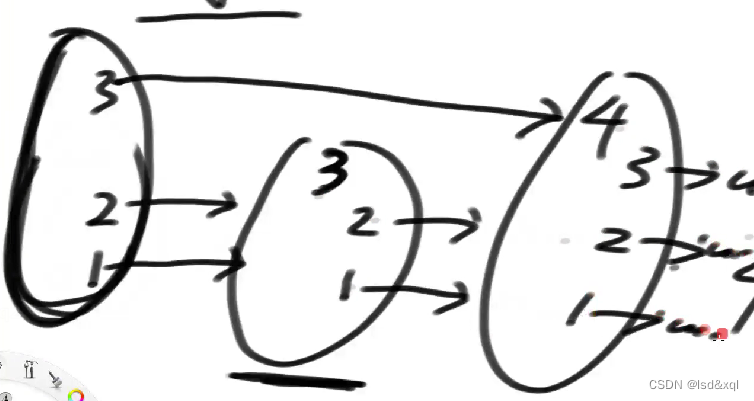
下面看一个比较正式的例子:
假设先来一个5,row出来层数为2,先创建层数2
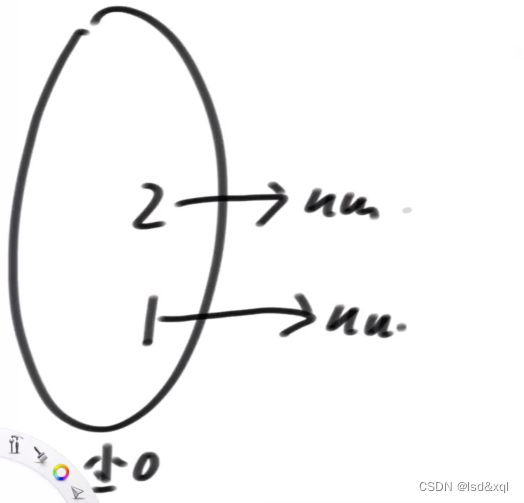
然后生成5的链表,有一层链表指向空,第二层链表指向空
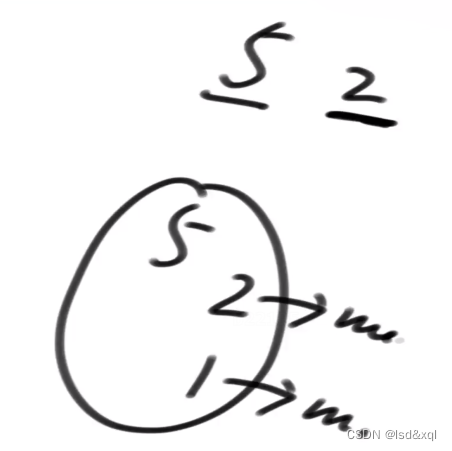
然后从第一个图中的高链表开始往下查,查到第一个大于5的节点,没有则进行挂载
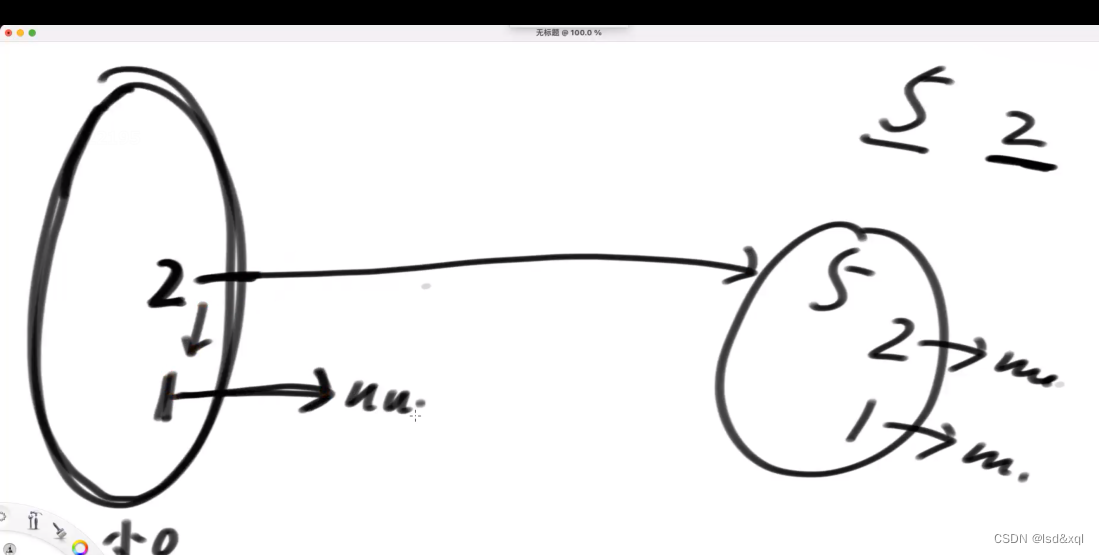
1链表里面找到第一个大于5的节点,没有则又连接起来
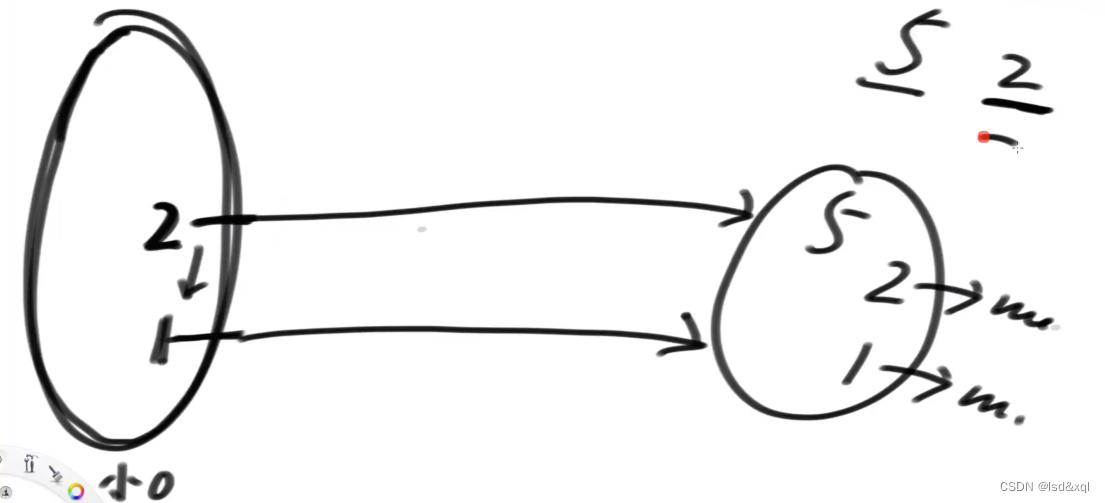
现在用户再给一个3,然后row出来4
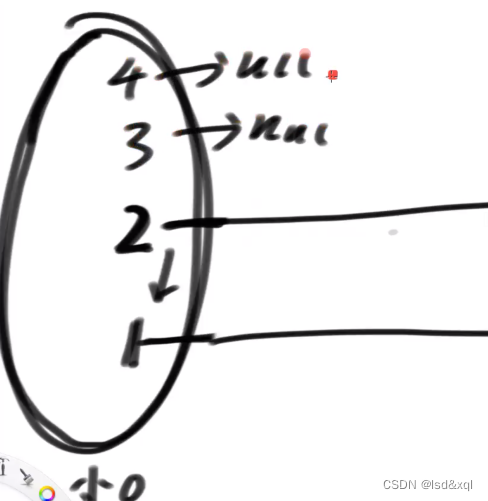
再建立出一个大的节点

从上图中的4开始找到第一个大于3的节点,发现没有则进行直接连接,然后从下一层的3开始找,发现也没有,则进行直连
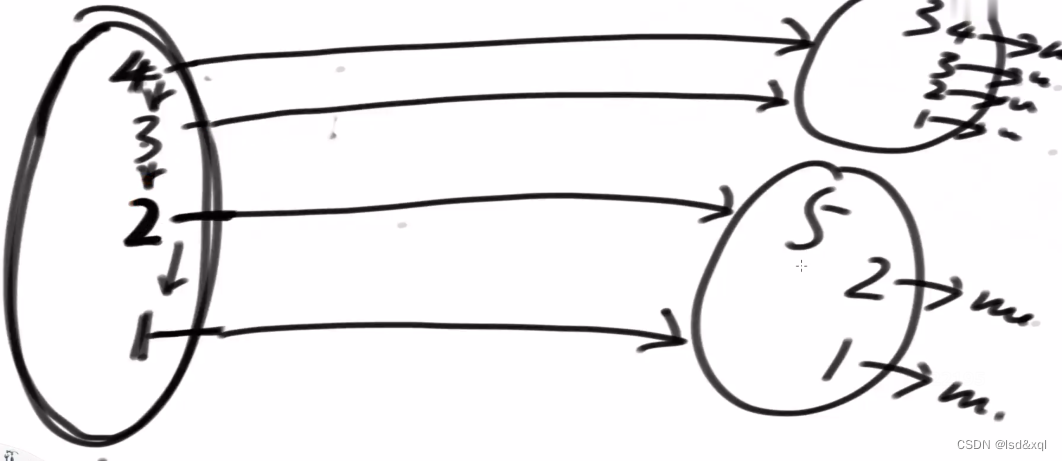
再找到2层里面第一个比3大的,发现有则让左边的2连接右边的3,右边3中的2连右下的5

以此类推最后的1也是那样

由此可以推导:
第一层数的个数为N,第二层为N/2,第三层为N/4依次类推,时间复杂度logN,用运气因素决定上层节点所处位置,上层移动一点下层跨过很多中间节点,把输入规律给屏蔽掉。时间复杂度推导可以画如下图:
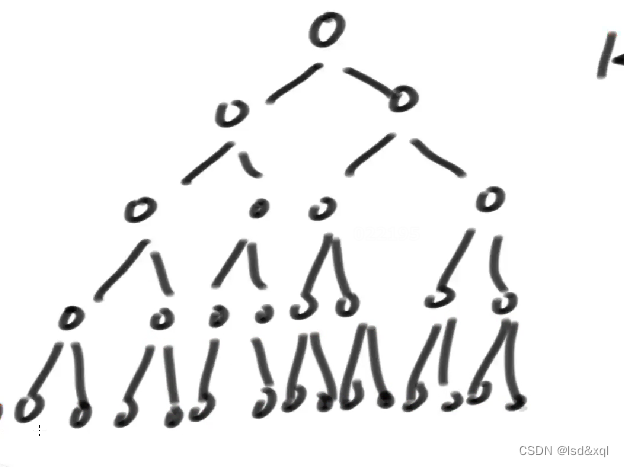
假设要找一个节点:
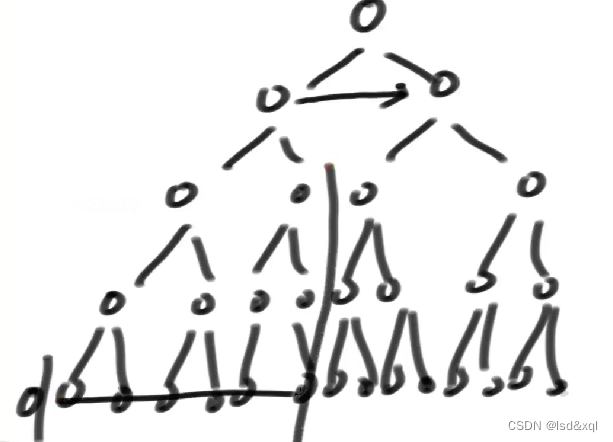
我第一层跨越后,那么我整棵树的左子树就可以完全屏蔽了,我每次跨都会淘汰掉相当多的节点往右跨则舍去左子树,往下跨则舍弃右子树部分。
public class SkipListMap {
// 跳表的节点定义
public static class SkipListNode<K extends Comparable<K>, V> {
public K key;
public V val;
//每个Node里面缓存多层链表
public ArrayList<SkipListNode<K, V>> nextNodes;
public SkipListNode(K k, V v) {
key = k;
val = v;
nextNodes = new ArrayList<SkipListNode<K, V>>();
}
// 遍历的时候,如果是往右遍历到的null(next == null), 遍历结束
// 头(null), 头节点的null,认为最小
// node -> 头,node(null, "") node.isKeyLess(!null) true
// node里面的key是否比otherKey小,true,不是false
public boolean isKeyLess(K otherKey) {
// otherKey == null -> false
return otherKey != null && (key == null || key.compareTo(otherKey) < 0);
}
public boolean isKeyEqual(K otherKey) {
return (key == null && otherKey == null)
|| (key != null && otherKey != null && key.compareTo(otherKey) == 0);
}
}
public static class SkipListMap<K extends Comparable<K>, V> {
private static final double PROBABILITY = 0.5; // < 0.5 继续做,>=0.5 停
//头节点
private SkipListNode<K, V> head;
//大小
private int size;
//最高层级
private int maxLevel;
public SkipListMap() {
//初始化
head = new SkipListNode<K, V>(null, null);
//第0层链表
head.nextNodes.add(null); // 0
size = 0;
maxLevel = 0;
}
// 从最高层开始,一路找下去,
// 最终,找到第0层的<key的最右的节点
private SkipListNode<K, V> mostRightLessNodeInTree(K key) {
if (key == null) {
return null;
}
int level = maxLevel;
SkipListNode<K, V> cur = head;
while (level >= 0) { // 从上层跳下层
// cur level -> level-1
//在这一层里小于key的最右的节点,这里cur接住返回值,是为了继续找下一层
cur = mostRightLessNodeInLevel(key, cur, level--);
}
return cur;
}
// 在level层里,如何往右移动
// 现在来到的节点是cur,来到了cur的level层,在level层上,找到<key最后一个节点并返回
private SkipListNode<K, V> mostRightLessNodeInLevel(K key,
SkipListNode<K, V> cur,
int level) {
SkipListNode<K, V> next = cur.nextNodes.get(level);
while (next != null && next.isKeyLess(key)) {
cur = next;
next = cur.nextNodes.get(level);
}
return cur;
}
public boolean containsKey(K key) {
if (key == null) {
return false;
}
SkipListNode<K, V> less = mostRightLessNodeInTree(key);
SkipListNode<K, V> next = less.nextNodes.get(0);
return next != null && next.isKeyEqual(key);
}
// 新增、改value
public void put(K key, V value) {
if (key == null) {
return;
}
// 0层上,最右一个,< key 的Node -> >key(注意是最下层第0层)
SkipListNode<K, V> less = mostRightLessNodeInTree(key);
//看找到的最右一个的下一个节点是否等于传入的key
SkipListNode<K, V> find = less.nextNodes.get(0);
if (find != null && find.isKeyEqual(key)) {
//如果相等则更新value,不用挂新记录
find.val = value;
} else { // find == null 8 7 9
//新来一条记录
size++;
int newNodeLevel = 0;
//row层数
while (Math.random() < PROBABILITY) {
newNodeLevel++;
}
// newNodeLevel如果大于maxlevel则最左边的head层数会升到和newNodeLevel一样高
while (newNodeLevel > maxLevel) {
head.nextNodes.add(null);
maxLevel++;
}
//新节点建立并且也建立那么多层
SkipListNode<K, V> newNode = new SkipListNode<K, V>(key, value);
for (int i = 0; i <= newNodeLevel; i++) {
newNode.nextNodes.add(null);
}
//从最高层开始
int level = maxLevel;
//最左节点
SkipListNode<K, V> pre = head;
while (level >= 0) {
// level 层中,找到最右的 < key 的节点
pre = mostRightLessNodeInLevel(key, pre, level);
//此处if判断是防止我原本左边的层数大于现在row出来的层数,那么就应该跳过
if (level <= newNodeLevel) {
//新节点在level层挂pre的下一个
newNode.nextNodes.set(level, pre.nextNodes.get(level));
//pre的下一个挂我自己
pre.nextNodes.set(level, newNode);
}
level--;
}
}
}
public V get(K key) {
if (key == null) {
return null;
}
SkipListNode<K, V> less = mostRightLessNodeInTree(key);
SkipListNode<K, V> next = less.nextNodes.get(0);
return next != null && next.isKeyEqual(key) ? next.val : null;
}
public void remove(K key) {
if (containsKey(key)) {
//存在削减最高层的情况
size--;
int level = maxLevel;
SkipListNode<K, V> pre = head;
while (level >= 0) {
//在本层找到最右的节点
pre = mostRightLessNodeInLevel(key, pre, level);
SkipListNode<K, V> next = pre.nextNodes.get(level);
// 1)在这一层中,pre下一个就是key
// 2)在这一层中,pre的下一个key是>要删除key
if (next != null && next.isKeyEqual(key)) {
// free delete node memory -> C++
// level : pre -> next(key) -> ...
pre.nextNodes.set(level, next.nextNodes.get(level));
}
// 在level层只有一个节点了,就是默认节点head
if (level != 0 && pre == head && pre.nextNodes.get(level) == null) {
head.nextNodes.remove(level);
maxLevel--;
}
level--;
}
}
}
public K firstKey() {
return head.nextNodes.get(0) != null ? head.nextNodes.get(0).key : null;
}
public K lastKey() {
int level = maxLevel;
SkipListNode<K, V> cur = head;
while (level >= 0) {
SkipListNode<K, V> next = cur.nextNodes.get(level);
while (next != null) {
cur = next;
next = cur.nextNodes.get(level);
}
level--;
}
return cur.key;
}
public K ceilingKey(K key) {
if (key == null) {
return null;
}
SkipListNode<K, V> less = mostRightLessNodeInTree(key);
SkipListNode<K, V> next = less.nextNodes.get(0);
return next != null ? next.key : null;
}
public K floorKey(K key) {
if (key == null) {
return null;
}
SkipListNode<K, V> less = mostRightLessNodeInTree(key);
SkipListNode<K, V> next = less.nextNodes.get(0);
return next != null && next.isKeyEqual(key) ? next.key : less.key;
}
public int size() {
return size;
}
}
// for test
public static void printAll(SkipListMap<String, String> obj) {
for (int i = obj.maxLevel; i >= 0; i--) {
System.out.print("Level " + i + " : ");
SkipListNode<String, String> cur = obj.head;
while (cur.nextNodes.get(i) != null) {
SkipListNode<String, String> next = cur.nextNodes.get(i);
System.out.print("(" + next.key + " , " + next.val + ") ");
cur = next;
}
System.out.println();
}
}
public static void main(String[] args) {
SkipListMap<String, String> test = new SkipListMap<>();
printAll(test);
System.out.println("======================");
test.put("A", "10");
printAll(test);
System.out.println("======================");
test.remove("A");
printAll(test);
System.out.println("======================");
test.put("E", "E");
test.put("B", "B");
test.put("A", "A");
test.put("F", "F");
test.put("C", "C");
test.put("D", "D");
printAll(test);
System.out.println("======================");
System.out.println(test.containsKey("B"));
System.out.println(test.containsKey("Z"));
System.out.println(test.firstKey());
System.out.println(test.lastKey());
System.out.println(test.floorKey("D"));
System.out.println(test.ceilingKey("D"));
System.out.println("======================");
test.remove("D");
printAll(test);
System.out.println("======================");
System.out.println(test.floorKey("D"));
System.out.println(test.ceilingKey("D"));
}
}







![【Flutter】引入网络图片时,提示:Failed host lookup: ‘[图片host]‘](https://img-blog.csdnimg.cn/img_convert/598930c90963d9f6bff62257d937d0b8.png)