需要源码和数据集请点赞关注收藏后评论区留言私信~~~

 与分簇、分类和标注任务不同，回归任务预测的不是有限的离散的标签值，而是无限的连续值。回归任务的目标是通过对训练样本的学习，得到从样本特征集到连续值之间的映射。如天气预测任务中，预测天气是冷还是热是分类问题，而预测精确的温度值则是回归问题。

一、回归任务

设样本集S={s_1,s_2,…,s_m}包含m个样本，样本s_i=(x_i,y_i)包括一个实例x_i和一个实数标签值y_i，实例由n维特征向量表示，即x_i=(x_i^(1),x_i^(2),…,x_i^(n))。 回归任务可分为学习过程和预测过程。

在学习过程，回归任务基于损失函数最小的思想，学习得到一个决策函数模型或神经网络模型。

决策函数回归模型要建立起合适的从实例特征向量到实数的映射函数Y=f(X)，X是定义域，它是所有实例特征向量的集合，Y是值域R。

神经网络回归模型要利用一定的网络结构N，学习到能够正确体现从实例到标签的映射关系的网络参数W，即得到合适的网络模型N(S,W)。

记测试样本为x=(x^(1),x^(2),…,x^(n))。在预测过程，决策函数回归模型依据决策函数Y=f(X)给予测试样本x一个预测标签值y ̂；神经网络回归模型将x馈入已经训练好的网络N(S,W)，从输出得到预测标签值y ̂。

回归常表现为用曲线或曲面（二维或高维）去逼近分布于空间中的各样本点，因此也称之为拟合。直线和平面可视为特殊的曲线和曲面。

二、线性回归与回归评价指标 

当用输入样本的特征的线性组合作为预测值时，就是线性回归（Linear Regression）。

记样本为s=(x,y)，其中x为样本的实例，x=(x^(1),x^(2),…,x^(n))，x^(j)为实例x的第j维特征，也直接称为该样本的第j维特征，y为样本的标签，在回归问题中，y是一个无限的连续值。

定义一个包含n个实数变量的集合{w^(0),w^(1),w^(2),…,w^(n)}，将样本的特征进行线性组合：

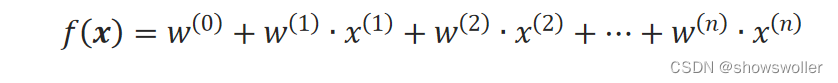
线性回归模型用向量表示为：

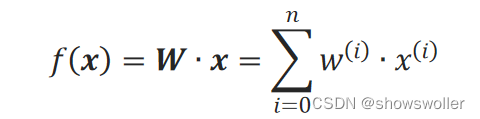
其中，x=(■8(x^(0)&■8(x^(1)&⋯)&x^(n)))^T为特征向量，并指定x^(0)=1，W=(w^(0) w^(1) … w^(n))为系数向量。向量W称为回归系数，负责调节各特征的权重，它就是要学习的知识。

线性回归是参数学习模型，因为它先假定了模型符合的决策函数，学习过程实际上求得该决策函数的最优参数值。

当只有1个特征时：

 

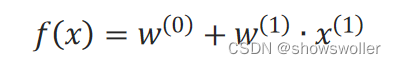
可看作是二维平面上的直线，此时x^(1)是直线的斜率，w^(0)是截距。

在二维平面上，让一条线去尽可能地贴近所有点，直接的想法是使所有点到该直线的距离和最小，使之最小的直线被认为是最“好”的。

 

距离l计算起来比较麻烦，一般采用更容易计算的残差s：

s_i=|y_i−f(x_i)|

式中，f(x)是拟采用的直线。容易理解，残差s与距离l之间存在等比例关系。因此，可以用所有点与该直线的残差和∑▒s_i代替距离和∑▒l_i作为衡量“贴近”程度的标准。

因为残差需要求绝对值，后续计算时比较麻烦，尤其是在一些需要求导的场合，因此常采用残差的平方作为衡量“贴近”程度的指标：

s_i^2=(y_i−y ̂_i)^2

残差称为绝对误差（Absolute Loss），残差平方称为误差平方（Squared Loss）。误差平方对后续计算比较方便，因此常采用所有点的误差平方和（Sum of Squared Error, SSE）作为损失函数来评价回归算法，该叫法与聚类的误差平方和损失函数相同。

还经常采用均方误差（Mean of Squared Error, MSE）作为损失函数，它是误差平方和除以样本总数。

线性回归中，不同的回归系数W确定了不同的线性模型，会带来不同的残差，因此，对于第i个样本来说，可将误差平方s_i^2记为s_i^2(W)。误差平方s_i^2(W)为实际值y_i与预测值f(x_i)之差的平方：

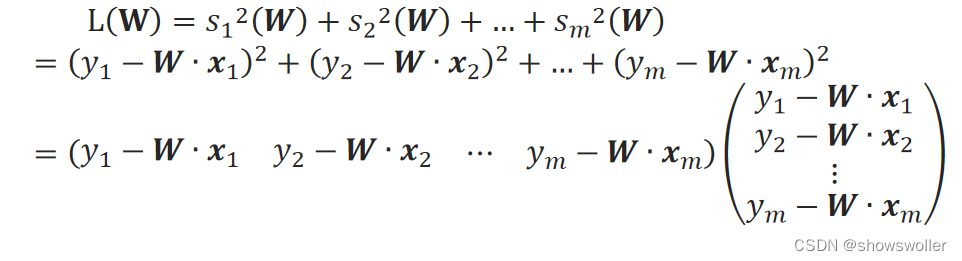
 因此，线性模型的求解，就是要求得使L(W)达到最小值时的W

三、线性回归温度与花朵数量实战

当温度处于15至40度之间时，数得某块草地上小花朵的数量和温度值的数据。现在要来找出这些数据中蕴含的规律，用来预测其它未测温度时的小花朵的数量。

线性回归拟合结果如下

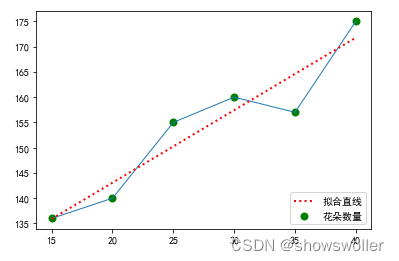
 部分代码如下

import numpy as np
from sklearn.metrics import mean_squared_error
175]
new_tempera = [18, 22, 33]
 
from sklearn import linear_model
reg = linear_model.LinearRegression()
temps = np.array(temperatures).reshape(-1,1)
reg.fit (temps, flowers)
temps_pred = reg.predict(temps)
print('MSE: %.2f' % mean_squared_error(flowers, temps_pred))
print("W(0):", reg.intercept_, "   W(1):", reg.coef_)
>>>  MSE: 17.80
W(0): 114.39047619047619    W(1): [1.43428571]
 
new_temps = np.array(new_tempera).reshape(-1,1)
reg.predict(new_temps)
>>> array([140.20761905, 145.9447619 , 161.72190476])

创作不易 觉得有帮助请点赞关注收藏~~~