创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!!
主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步!
给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ

目录
- 问题描述
- 问题分析
- 代码实现
- 复杂性分析
问题描述
给定一个序列,对其按照大小递增或递减进行排序
问题分析
找到一个基准值x,将序列中小于x的元素放在左侧,将大于x的元素放在右侧,对左右两个子序列分别重复同样的操作,直至子序列的长度为1或0时结束
步骤如下:
-
选择基准,一般选择第一个元素作为基准,或者随机选择
-
将数组划分为两个部分,小于等于基准点的元素在左边,大于基准点的元素在右边
从数组的第二个元素开始遍历,如果当前元素小于基准,就交换它和第一个元素的位置。
这样,所有小于基准的元素都在基准的左边,所有大于基准的元素都在基准的右边。
- 然后对左右两个部分分别进行递归排序
快速排序就是先将⼀个元素排好序,然后再将剩下的元素排好序
选择一个基准元素,将数组分成两部分,使得一部分的元素都比基准元素小,另一部分的元素都比基准元素大,然后对这两部分分别进行快速排序。
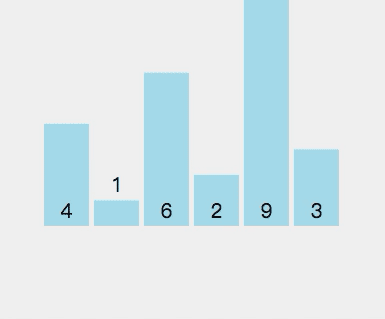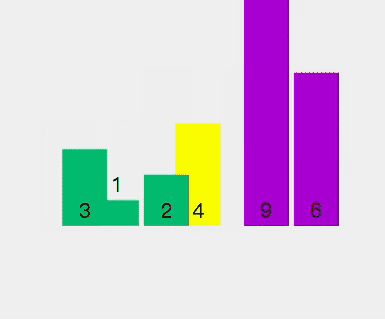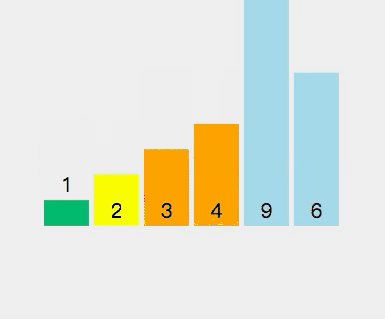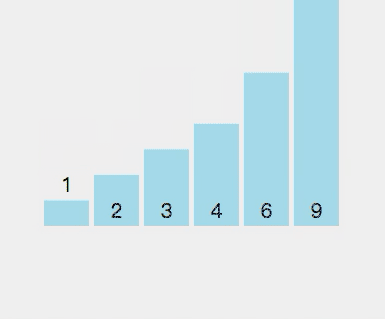
代码实现
#include <iostream>
using namespace std;
void QuickSort(int arr[], int left, int right)
{
if (left >= right) {
return;
}
int mark = arr[left]; //基准值
int l = left;
int r = right;
int t = 0;
while (l < r)
{
while (l < r && arr[r] >= mark) {//循环找到前序列大于基准的值
r--;
}
while (l < r && arr[l] <= mark) {
l++;
}
if (l < r) {
t = arr[l]; arr[l] = arr[r]; arr[r] = t;
}
}
t = arr[l]; arr[l] = arr[left]; arr[left] = t;
QuickSort(arr, left, l - 1);
QuickSort(arr, l + 1, right);
}
int main()
{
int arr[5] = { 3,6,5,1,8 };
QuickSort(arr,0,4);
for (int v : arr)
{
cout << v << " ";
}cout << endl;
return 0;
}

这里介绍一下我看过的labuladong的算法笔记中的内容:
快速排序的基本框架:
void quicksort(int nums[], int lo, int hi) {
if (lo >= hi) {
return;
}
// 对 nums[lo..hi] 进⾏切分
// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
int p = partition(nums, lo, hi);
// 去左右⼦数组进⾏切分
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}
复杂性分析
- 如果每次划分都产生
两个n-1和1个元素的区间:
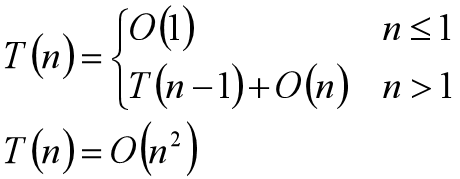
- 如果每次划分所取的基准恰好为中值:
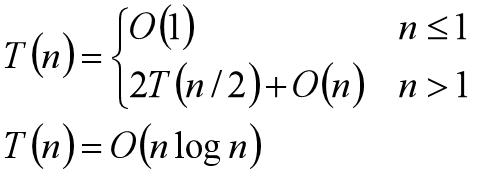
快速排序的时间复杂度在最坏情况下是O(n^2),但是在平均情况下,时间复杂度是O(n log n)

在数组中随机选出一个元素作为划分基准,这样可以使划分基准的选择是随机的,从而可以期望划分是较对称的

| 大家的点赞、收藏、关注将是我更新的最大动力! 欢迎留言或私信建议或问题。 |
| 大家的支持和反馈对我来说意义重大,我会继续不断努力提供有价值的内容!如果本文哪里有错误的地方还请大家多多指出(●'◡'●) |