使用迭代方式解决汉诺塔问题（Java语言）

news2025/1/13 8:07:31

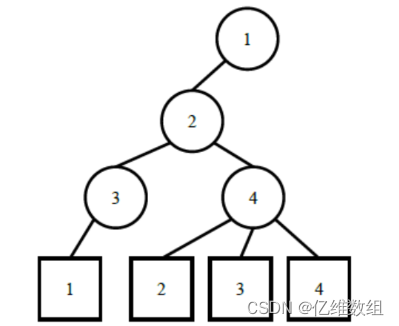
汉诺塔问题解决

迭代介绍

汉诺塔问题解决

在这个Java示例中，我们使用了一个Stack数据结构来模拟递归调用的过程。hanoiIterative函数接受盘子数量n以及三个柱子的名称作为参数，并在迭代过程中模拟汉诺塔的移动操作。moveDisk函数用于模拟盘子的移动操作。

示例代码中的main函数演示了如何使用hanoiIterative函数来解决汉诺塔问题。你可以根据需要调整盘子数量和柱子的名称来执行不同规模的问题。

import java.util.Stack;

public class HanoiTower01 {

    public static void hanoiIterative(int n, char source, char auxiliary, char target) {
        if (n % 2 == 0) {
            char temp = auxiliary;
            auxiliary = target;
            target = temp;
        }

        int numMoves = (int) Math.pow(2, n) - 1;
        for (int move = 1; move <= numMoves; move++) {
            if (move % 3 == 1) {
                moveDisk(source, target);
            } else if (move % 3 == 2) {
                moveDisk(source, auxiliary);
            } else {
                moveDisk(auxiliary, target);
            }
        }
    }

    public static void moveDisk(char source, char target) {
        System.out.println("Move disk from " + source + " to " + target);
    }

    public static void main(String[] args) {
        int n = 6; // 汉诺塔的盘子数量
        char source = 'A'; // 源柱子的名称
        char auxiliary = 'B'; // 辅助柱子的名称
        char target = 'C'; // 目标柱子的名称

        hanoiIterative(n, source, auxiliary, target);
    }
}

迭代介绍

在计算机领域中，"迭代"是一种重复执行一组指令或操作的过程的概念。这是一种基本的控制流程，用于处理循环和重复性任务。迭代是计算机程序中的常见编程模式，它允许程序在某些条件下反复执行一段代码，直到满足特定的终止条件。

以下是关于迭代的一些重要概念和含义：

迭代过程：迭代是一种过程，其中一组指令被重复执行，通常是通过循环结构实现的。这个过程一直持续，直到满足终止条件。
循环结构：循环是一种控制结构，它允许程序反复执行一段代码块。在计算机编程中，有各种各样的循环结构，如for循环、while循环和do-while循环，它们都用于实现迭代。
迭代器：迭代器是一种数据结构，用于遍历集合中的元素，如数组、链表或其他数据结构。通过迭代器，程序可以依次访问集合中的每个元素，从而实现对集合的迭代操作。
终止条件：在迭代过程中，通常需要定义一个或多个终止条件，以确定何时停止迭代。这些条件是根据问题的要求和逻辑来定义的。
迭代 vs. 递归：迭代和递归都是处理重复性任务的方式，但它们的实现方式不同。迭代使用循环结构和栈来重复执行代码，而递归使用函数自身来实现任务的重复。
性能考虑：在一些情况下，迭代可能比递归更具性能优势，因为递归调用会增加栈的深度，可能导致栈溢出。迭代通常更适用于处理大规模数据和算法。