⛲️
路程问题是根据速度、时间、路程之间的关系,研究物体相向、相背和同向运动的问题,解决路程问题常用方法:
(1)分解。将综合性的题目先分解成若干个基本题,再按其所属类型,直接利用基本数量关系解题。
(2)图示。将题中复杂的情节通过线段图清楚地表示出来,帮助分析思考。
(3)简化。对于一些较复杂的问题,解答时可以先退一步,考虑最基本的情况,复杂的问题简单化,从而找到解题途径。
(4)找规律。有些路程问题,物体运动具有一定的规律,解题时,如果能先找出运动规律,问题就能顺利破解。
(5)沟通。将路程问题和比例问题、分数问题相互沟通,利用份数来建立联系,灵活、巧妙地找到1份的量,使难题变易。
题型1 定速路程问题
考向1 巧抓等量关系
思路:根据题干信息进行问题转化,也可利用图示法找到对应的等量关系来快速求解。
考向2 巧用速度比
思路:在路程问题中,先利用比例关系来找到等量关系,再按照份数进行求解,可以将题目进行简化,在考场上赢得宝贵的时间。
考向3 路程盈亏问题
思路:盈亏问题是两次分配产生盈亏,解题方法是(盈+亏)÷ 分配差,得到分配对象有多少个。其他类似盈亏问题的应用题也可以表述为:总量固定,一个量增减,则另外一 个量减增。
考向4 整体法求路程
思路:当不好求每一段行驶的路程的时候,可以采用整体思路利用:
总时间
×
总速度
=
总路程
总时间×总速度=总路程
总时间×总速度=总路程来进行求解。
题型2 变速路程问题
考向1 同一路程变速问题
思路:解决同一路程变速问题的常用方法有:
(1)方程组法;(2)比例法;(3)法宝公式法;(4)等面积法;(5)假设法
考向2 不同路程变速向题
思路:对于不同路程的变速问题,通常要用假设转化的方法找到比例,达到化简的目的。
题型3 往返路程问题
思路:多次往返相遇问题的技巧是抓住“路程和”来建立等量关系或寻找比例关系。假设相遇次数为几次,两端的路程为S。
记住口诀:
同向往返相遇两人的路程和为
S
路程和
=
2
n
S
S_{路程和}=2nS
S路程和=2nS;
反向往返相遇两人的路程和为
S
路程和
=
(
2
n
−
1
)
S
S_{路程和}=(2n-1)S
S路程和=(2n−1)S。
题型4 假设法解路程问题
思路:路程问题中路程、速度、时间三个未知量的关系是知二求一。当有两个未知量的时候,可以利用假设法(设数法)来进行求解,此时主要求的是比例。
题型5 三个对象的路程问题
考向1 两人同向,一人反向
思路:根据题目进行画图,找到三人之间路程的等量关系。
考向2 三个对象同向
思路:看到三个对象同向同起点运动,要用比例法解决。
题型6 流水行船问题
思路:
V
顺
=
V
静
+
V
水
,
V
逆
=
V
静
−
V
水
,
V
静
=
V
顺
+
V
逆
2
,
V
水
=
V
顺
−
V
逆
2
V_顺=V_静+V_水,V_逆=V_静-V_水,V静=\frac{V_顺+V_逆}{2},V_水=\frac{V_顺-V_逆}{2}
V顺=V静+V水,V逆=V静−V水,V静=2V顺+V逆,V水=2V顺−V逆,
特别提醒:水中掉落物体(漂浮)时,从落水到发现与从发现到找到的时间相同!
题型7 跑圈问题
思路:记住口诀:同向时“路程差”为一圈,反向时“路程和”为一圈;起点相遇找速度比;不同起点第一次相遇和追及当成直线型,第二次开始当成“同起点”的跑圈问题。
👊
- 路程s,速度v和时间t之间的关系: s = v t , t = s v , v = s t s=vt,t=\frac{s}{v},v=\frac{s}{t} s=vt,t=vs,v=ts
- 相对速度:同向而行,相对速度= ∣ V 甲 − V 乙 ∣ |V_甲-V_乙| ∣V甲−V乙∣;相向而行,相对速度= V 甲 + V 乙 V_甲+V_乙 V甲+V乙
- 速度相同,时间比等于路程比,时间相同,速度比等于路程比;路程相同,速度比等于时间的反比
- 顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度
- 追及与相遇问题:
①直线型路程:
相遇: S 相遇 = S 甲 + S 乙 = ( v 甲 + v 乙 ) t S_{相遇}=S_甲+S_乙=(v_甲+v_乙)t S相遇=S甲+S乙=(v甲+v乙)t;
追及: S 追及 = S 甲 − S 乙 = ( v 甲 − v 乙 ) t S_{追及}=S_甲-S_乙=(v_甲-v_乙)t S追及=S甲−S乙=(v甲−v乙)t
②圆圈型路程:
同向运动:同一起点出发,顺时针方向跑,第一次在B点遇上( V 甲 > V 乙 V_甲>V_乙 V甲>V乙)。等量关系(经历时间相同): S 甲 − S 乙 = S S_甲-S_乙=S S甲−S乙=S。甲乙每相遇一次,甲比乙多跑一圈,若相遇n次,则有 S 甲 − S 乙 = n S ; S 甲 S 乙 = n S + S 乙 S 乙 S_甲-S_乙=nS;\frac{S_甲}{S_乙}=\frac{nS+S_乙}{S_乙} S甲−S乙=nS;S乙S甲=S乙nS+S乙。

逆向运动:同一起点出发,相反方向跑,第一次在B点遇上。等量关系: S 甲 + S 乙 = S S_甲+S_乙=S S甲+S乙=S。甲乙每相遇一次,甲与乙路程之和为一圈,若相遇n次,则有 S 甲 + S 乙 = n S ; V 甲 V 乙 = S 甲 S 乙 = n S − S 乙 S 乙 S_甲+S_乙=nS;\frac{V_甲}{V_乙}=\frac{S_甲}{S_乙}=\frac{nS-S_乙}{S_乙} S甲+S乙=nS;V乙V甲=S乙S甲=S乙nS−S乙

⛲️
路程问题是联考常考题型,题型难度属于中等偏上,以直线型和圆圈型两大类型为主线,以相遇与追及为模板。
1.路程s、速度v、时间t之间的关系:
s
=
v
t
,
t
=
s
v
,
v
=
s
t
s=vt,t=\frac{s}{v},v=\frac{s}{t}
s=vt,t=vs,v=ts
2.对于直线型的路程问题:
(1)相遇
s
相遇
=
S
1
+
S
2
=
v
1
t
+
v
2
t
=
(
v
1
+
v
2
)
t
s_{相遇}=S_1+S_2=v_1t+v_2t=(v_1+v_2)t
s相遇=S1+S2=v1t+v2t=(v1+v2)t
(2)追赶
s
追及
=
S
1
−
S
2
=
v
1
t
−
v
2
t
=
(
v
1
−
v
2
)
t
s_{追及}=S_1-S_2=v_1t-v_2t=(v_1-v_2)t
s追及=S1−S2=v1t−v2t=(v1−v2)t
3.对于圆圈型的路程问题:(从同一起点同时出发,周长为s,相遇一次时间为t)
反向运动:
S
=
S
1
+
S
2
=
v
1
+
v
2
t
=
(
v
1
+
v
2
)
t
S=S_1+S_2=v_1+v_2t=(v_1+v_2)t
S=S1+S2=v1+v2t=(v1+v2)t;
同向运动:
S
=
S
1
−
S
2
=
v
1
t
−
v
2
t
=
(
v
1
−
v
2
)
t
S=S_1-S_2=v_1t-v_2t=(v_1-v_2)t
S=S1−S2=v1t−v2t=(v1−v2)t。
4.顺水、逆水问题:
v
顺水
=
v
船
+
v
水
;
v
逆水
=
v
船
−
v
水
v_{顺水}=v_船+v_水;v_{逆水}=v_船-v_水
v顺水=v船+v水;v逆水=v船−v水
5.相对速度(两个物体运动时,可将一个作为参照物,看成相对静止的)
同向运动:
v
同向
=
v
1
−
v
2
v_{同向}=v_1-v_2
v同向=v1−v2;
相向运动:
v
相向
=
v
1
+
v
2
v_{相向}=v_1+v_2
v相向=v1+v2。
【评注】路程问题主要涉及路程、时间、速度三者的关系,一般以时间或路程为等量关系来列方程路程又分为直线型、圆圈型、顺水逆水、相对速度等题型。
此外,路程问题可延伸至工程问题:路程可以看做工作量,时间可以看做工作时间,速度可以看做工作效率。
⛲️
(一)直线路程问题
一、考点讲解
- 基本公式
s = v t , v = s t , t = s v s=vt,v=\frac{s}{t},t=\frac{s}{v} s=vt,v=ts,t=vs - 直线相遇公式
S 相遇 = S 1 + S 2 = v 1 t + v 2 t = ( v 1 + v 2 ) t S_{相遇}=S_1+S_2=v_1t+v_2t=(v_1+v_2)t S相遇=S1+S2=v1t+v2t=(v1+v2)t - 直线追及公式
S 追及 = S 1 − S 2 = v 1 t − v 2 t = ( v 1 − v 2 ) t S_{追及}=S_1-S_2=v_1t-v_2t=(v_1-v_2)t S追及=S1−S2=v1t−v2t=(v1−v2)t
二、考试解读
- 路程问题在考试中出现的频率较高,做路程问题,首先根据题意要画出示意图,标注已知对象的相关信息,其次建立等量关系,常用的是时间或路程为基本等量式。
- 路程问题的重点在于设未知数和找等量关系,尤其多对象运动问题,对考生要求较高。
- 难点在于变速运动的路程问题及图像的路程问题。
- 考试频率级别:高。
三、命题方向
- 直线相遇
思路:两车相向而行,相遇时间=路程和÷速度和或相遇时间=路程差÷速度差。 - 直线往返相遇
思路:对于多次往返相遇的题目,要根据两人的路程关系列方程求解。 - 直线追及
思路:两个运动物体在不同地点同时出发(或者在同一地点而不是同时出发,或者在不同地点又不是同时出发)做同向运动,在后面的行进速度要快些,在前面的行进速度较慢些,在一定时间之内,后面的追上前面的物体。这类应用题就叫作追及问题,根据追及时间与路程的关系列方程,所用公式为:路程差 = 速度差×追及时间. - 直线变速
思路:变速运动难度较大,主要根据速度变化前后的时间关系列方程。
(二)水中行船问题
一、考点讲解
- 船顺流时速度: v 顺 = v 船 + v 水 v_顺=v_船+v_水 v顺=v船+v水
- 船逆流时速度: v 逆 = v 船 − v 水 v_逆=v_船-v_水 v逆=v船−v水
二、考试解读
- 水中行船问题要看清楚水流方向,分清是顺水还是逆水。
- 难点在于水流何时对船有影响。
- 考试频率级别:中。
三、命题方向
- 与水速有关
思路:单一物体在水上运动时,时间与水速有关。 - 与水速无关
思路:多个物体在水中运动,无论是相遇还是追及,都与水速无关。因为水速抵消了。
(三)相对速度问题
一、考点讲解
- 相对速度: v = v 1 + v 2 v=v_1+v_2 v=v1+v2
- 相对速度: v = v 1 − v 2 v=v_1-v_2 v=v1−v2
二、考试解读
- 当出现多个物体同时运动时,将某个物体看成“静止”的,当作参照物,利用相对速度分析会比较简便。
- 路程问题的难点在于运动的方向,对考生要求较高。
- 考试频率级别:低。
三、命题方向
- 队伍行军
思路:可以将队伍看成静止的,通讯员转化为相对运动分析即可。 - 火车与行人
思路:将行人看成静止的,然后火车转化为相对运动分析即可。 - 发车间隔
思路:将行人看成静止的,然后公交车转化为相对运动分析即可。
(四)火车过桥问题
一、考点讲解
火车过桥时间:
t
=
l
车
+
l
桥
v
t=\frac{l_车+l_桥}{v}
t=vl车+l桥
二、考试解读
- 火车过桥比较简单,按公式计算即可。
- 由于火车速度不变,时间与长度成比例,采用比例法分析比较简单。
- 考试频率级别:低。
三、命题方向
- 火车过桥
思路:根据公式 t = l 车 + l 桥 v t=\frac{l_车+l_桥}{v} t=vl车+l桥,列方程求解分析。
(五)圆圈路程问题
一、考点讲解
-
同向同起点:甲乙每相遇一次,甲比乙多跑一圈
相遇时的等量关系: s 甲 − s 乙 = s s_甲-s_乙=s s甲−s乙=s(经历时间相同)
甲、乙每相遇一次,甲比乙多跑一圈,若相遇n次,则有 s 甲 − s 乙 = n s s_甲-s_乙=ns s甲−s乙=ns
v 甲 v 乙 = s 甲 s 乙 = s 乙 + n s s 乙 = 1 + n s s 乙 \frac{v_甲}{v_乙}=\frac{s_甲}{s_乙}=\frac{s_乙+ns}{s_乙}=1+\frac{ns}{s_乙} v乙v甲=s乙s甲=s乙s乙+ns=1+s乙ns -
反向同起点:每相遇一次,甲与乙路程之和为一圈
相遇时的等量关系: s 甲 + s 乙 = s s_甲+s_乙=s s甲+s乙=s
每相遇一次,甲与乙路程之和为一圈,若相遇n次有 s 甲 + s 乙 = n s s_甲+s_乙=ns s甲+s乙=ns
v 甲 v 乙 = s 甲 s 乙 = n s − s 乙 s 乙 = n s s 乙 − 1 \frac{v_甲}{v_乙}=\frac{s_甲}{s_乙}=\frac{ns-s_乙}{s_乙}=\frac{ns}{s_乙}-1 v乙v甲=s乙s甲=s乙ns−s乙=s乙ns−1
【解题技巧】在做圆圈型追及相遇题时,求第k次相遇情况,可以将第k-1次相遇看成起点进行分析考虑。
二、考试解读
- 圆圈型路程问题比较难,容易出错,但考试只要求掌握定速的圆圈型问题。
- 难点在于运动方向以及是否同起点运动,对考生要求较高。
- 考试频率级别:低。
三、命题方向
- 同起点
思路:如果起点相同,当同向运动时,每相遇一次,路程差为一圈;当反向运动时,每相遇一次,路程和为一圈。 - 不同起点
思路:如果两人不同起点,则第一次相遇后,就变成同起点的运动了。
(六)图像路程问题
一、考点讲解
s
=
v
t
,
v
=
s
t
,
t
=
s
v
s=vt,v=\frac{s}{t},t=\frac{s}{v}
s=vt,v=ts,t=vs
- v-s 图
(1)匀速运动(见图2-3)
(2)变速运动(见图2-4,图2-5)



- s-t 图
(1)匀速运动(见图2-6,图2-7)


(2)加速运动(见图2-11,图2-12)

二、考试解读
- 利用图像描述物体的速度、路程、时间关系。首先要看清横坐标、纵坐标分别表示什么物理量,再从图像中读出速度、路程或时间的大小。
- 路程问题的难点在于根据图像区分是匀速运动还是非匀速运动。
- 考试频率级别:低。
三、命题方向
-
v-s 图
思路:对于v-s 图,如果图像是水平的直线,则表示匀速运动,其他直线或曲线表示变速运动。 -
s-t 图
思路:对于s-t 图,如果图像为直线时,表示匀速运动,直线的斜率表示速度,当斜率为0时,物体静止;如果图像为曲线,表示变速运动。 -
v-t 图
思路:对于v-t 图,当图像为直线时,直线的斜率表示加速度,当斜率为零时,表示匀速运动,斜率不为零时,表示匀变速运动;当图像为曲线时,表示非匀变速运动。
👑
一、普通匀速直线运动问题:路程=速度×时间;平均速度=总路程÷总时间
【解题提示】根据题意画出简单的示意图,设未知数列方程求解,同时注意路程、时间、速度三者中的恒定量,将问题转化为比例关系求解。
注:行程问题中常用的比例关系:
① 时间相同时,速度比等于路程比;
② 速度相同时,时间比等于路程比;
③ 路程相同时,速度比等于时间的反比。
二、行程问题中的相遇、追赶题型
1 直线型相遇、追赶问题
【解题提示】此类问题比较常见,根据题意画出简单示意图,抓住等量关系(一般是时间和路程),列方程求解。
(1)同时相向而行
问题表述:甲、乙两人同时分别从A、B两地相向而行,在C点相遇会合。
等量关系:
S
甲
+
S
乙
=
S
A
B
⇒
(
V
甲
+
V
乙
)
t
=
S
A
B
,
V
甲
V
乙
=
S
甲
S
乙
=
A
C
B
C
(
时间相同
)
S_甲+S_乙=S_{AB}\Rightarrow(V_甲+V_乙)t=S_{AB},\frac{V_甲}{V_乙}=\frac{S_甲}{S_乙}=\frac{AC}{BC}(时间相同)
S甲+S乙=SAB⇒(V甲+V乙)t=SAB,V乙V甲=S乙S甲=BCAC(时间相同)
(2)追赶问题
问题表述:甲、乙相距AC时甲追赶乙,并最终在B点追上乙。
等量关系:
S
甲
−
S
乙
=
S
A
C
⇒
(
V
甲
−
V
乙
)
t
=
S
A
C
,
V
甲
V
乙
=
S
甲
S
乙
=
A
B
B
C
(
时间相同
)
S_甲-S_乙=S_{AC}\Rightarrow(V_甲-V_乙)t=S_{AC},\frac{V_甲}{V_乙}=\frac{S_甲}{S_乙}=\frac{AB}{BC}(时间相同)
S甲−S乙=SAC⇒(V甲−V乙)t=SAC,V乙V甲=S乙S甲=BCAB(时间相同)
2.圆圈型(操场)相遇、追赶问题
(1)同向(设圆周长为S)
等量关系:
S
甲
−
S
乙
=
S
S_甲-S_乙=S
S甲−S乙=S(假设甲的速度较快)
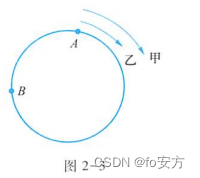
如图2-3,甲 、乙每相遇一次,甲比乙多跑一圈,若n次相遇,则有
S
甲
−
S
乙
=
n
S
,
V
甲
V
乙
=
S
甲
S
乙
=
S
乙
+
n
S
S
乙
S_甲-S_乙=nS,\frac{V_甲}{V_乙}=\frac{S_甲}{S_乙}=\frac{S_乙+nS}{S_乙}
S甲−S乙=nS,V乙V甲=S乙S甲=S乙S乙+nS
(2)逆向
等量关系:
S
甲
+
S
乙
=
S
S_甲+S_乙=S
S甲+S乙=S
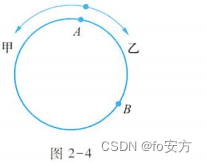
如图2-4,每次相遇,甲、乙的路程之和为一圈,若相遇n次,则有
S
甲
+
S
乙
=
n
S
,
V
甲
V
乙
=
S
甲
S
乙
=
n
S
−
S
乙
S
乙
S_甲+S_乙=nS,\frac{V_甲}{V_乙}=\frac{S_甲}{S_乙}=\frac{nS-S_乙}{S_乙}
S甲+S乙=nS,V乙V甲=S乙S甲=S乙nS−S乙
【解题技巧】在做圆圈型追及相遇问题时,求第k次相遇情况,可以将(k-1)次相遇看成起点进行分析考虑。
三、船在水中航行问题
V
顺水
=
V
船
+
V
水
V_{顺水}=V_{船}+V_{水}
V顺水=V船+V水;
V
逆水
=
V
船
−
V
水
V_{逆水}=V_{船}-V_{水}
V逆水=V船−V水;
V
船
=
V
顺水
+
V
逆水
2
V_{船}=\frac{V_{顺水}+V_{逆水}}{2}
V船=2V顺水+V逆水;
V
水
=
V
顺水
−
V
逆水
2
V_{水}=\frac{V_{顺水}-V_{逆水}}{2}
V水=2V顺水−V逆水。


💂
-
基本公式
路程 s = 速度 v × 时间 t , 路程s=速度v×时间t, 路程s=速度v×时间t, 速度 v = 路程 s 时间 t , 速度v=\frac{路程s}{时间t}, 速度v=时间t路程s, 时间 t = 路程 s 速度 v 时间t=\frac{路程s}{速度v} 时间t=速度v路程s -
相遇和追及
相向运动的两物体相对速度为两速度之和,同向运动的两物体相对速度为两速度之差。
相遇时间 = 相遇距离 速度之和 v 1 + v 2 相遇时间=\frac{相遇距离}{速度之和v_1+v_2} 相遇时间=速度之和v1+v2相遇距离
追及时间 = 追及距离 速度之差 v 1 − v 2 追及时间=\frac{追及距离}{速度之差v_1-v_2} 追及时间=速度之差v1−v2追及距离 -
环形道路
两人自同一起点沿环形跑道相向/同向行进,直至相遇,有如下等量关系:
相向时:甲路程 + 乙路程 = 环形周长
同向时:快者路程 ― 慢者路程 = 环形周长
事实上,相向跑圈每相遇一次,两人路程之和为环形跑道周长;同向跑圈每相遇一次,快者比慢者多跑一个环形跑道周长。 -
顺水/逆水行船
逆水行船时:实际速度为 v 船 − v 水 v_船-v_水 v船−v水;顺水行船是:实际速度为 v 船 + v 水 v_船+v_水 v船+v水。 -
火车错车/过桥过洞
相向错车: t = 车长之和 l 1 + l 2 速度之和 v 1 + v 2 t=\frac{车长之和l_1+l_2}{速度之和v_1+v_2} t=速度之和v1+v2车长之和l1+l2
同向超车: t = 车长之和 l 1 + l 2 速度之差 v 1 − v 2 t=\frac{车长之和l_1+l_2}{速度之差v_1-v_2} t=速度之差v1−v2车长之和l1+l2
火车过桥/过山洞: t = l 山洞 / 桥梁 + l 火车 v t=\frac{l_{山洞/桥梁}+l_{火车}}{v} t=vl山洞/桥梁+l火车
💭
- 相遇问题,反向行驶,第一次遇见路程和等于总路程
相遇时间=总路程 ÷ (甲速 + 乙速)
总路程 = (甲速 + 乙速)× 相遇时间 - 追及问题,每追上一次表示速度快的比慢的多跑一圈
追及时间 = 追及路程 ÷ (快速 - 慢速)
追及路程 = (快速 - 慢速)× 追及时间
🌐
解题提示:根据题意画图,找等量关系(一般是时间和路程),列方程求解。
常见类型有:
类型一:

A 的行程 + B 的行程 = 甲、乙两地的距离
相遇过程:相遇时间=
距离之和
速度之和
\frac{距离之和}{速度之和}
速度之和距离之和
类型二:同向
(圆圈型)每相遇一次,甲比乙多跑一圈

类型三:逆向

解题技巧:在做圆圈型追及相遇题时,在求第 k 次相遇情况时,可以将 k-1 次相遇看成起点进行分析考虑。




![[hello,world]这个如何将[ ] 去掉](https://img-blog.csdnimg.cn/fe1f55d13c3b497f8cab63cfed4c85e8.png#pic_center)


![[H5动画制作系列] Sprite及Text Demo](https://img-blog.csdnimg.cn/9ed8797be3244513acd8cba2a3736fe7.png)