一 背景介绍
- 日常会有很多定量分析的场景,然而也会有一些定性分析的场景
- 针对定性分析的场景,预测者只能通过主观判断分析能力来推断事物的性质和发展趋势
- 然而针对个人的直觉和虽然能够有一定的协助判断效果,但是很难量化到指标做后期的复用 AHP层次分析法可以将定性分析和定量分析更好地融合
二 AHP简单介绍
AHP(Analytic Hierarchy Process,简称AHP)中文名称为层次分析法,是美国运筹学匹兹堡大学教授萨蒂于20世纪70年代提出,用于将决策相关的因素划分不同层次,做定性和定量分析结合的方法。
其主要的思路为将决策分层三个层次:
- 最高层:最终决策的目的、要解决的问题,即目标层
- 中间层:主因素,考虑的因素、决策的准则层
- 最低层:决策时的备选方案,也可为中间层的子因素,方案层
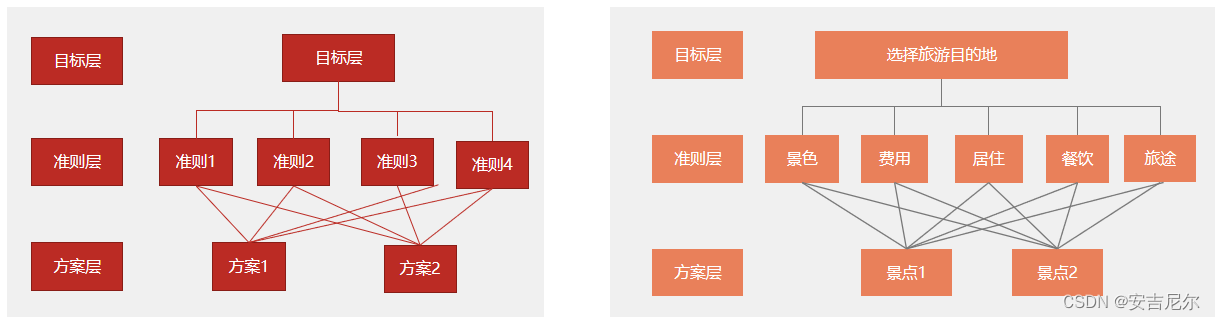
整体决策的思路为:
1.构建层次评价模型:有明确的准则(指标)、可选方案、目标
2.基于AHP确定指标定权重
3.基于指标权重,计算量化后的方案选择
其中指标权重确认的整个步骤为:
1.构建指标判断矩阵(也就是指标两两比较,用数字区分重要程度)
2.进行权重的计算
3.进行一致性校验(保证比较是合理的)
4.进行层次总排序
5.进行方案选择
计算原理详细步骤细节建议可以参考相关书籍内容

三 相关代码
说明:
- 由于做测试数据结果验证,做了特殊的手工入口录入
- 可以根据实际录入需求做导入对象替换,或者原始数据数组粘贴对象替换
调试代码参考
import numpy as np
# 计算指标权重的判断矩阵
def calculate_weights(comparison_matrix):
num_indicators = comparison_matrix.shape[0]
eigenvalues, eigenvectors = np.linalg.eig(comparison_matrix)
max_eigenvalue_index = np.argmax(eigenvalues)
max_eigenvector = eigenvectors[:, max_eigenvalue_index]
weights = max_eigenvector / np.sum(max_eigenvector)
return weights
# 输入当前指标对应不同方案的打分判断矩阵
def input_comparison_matrix(indicator):
num_solutions = len(indicator)
comparison_matrix = np.zeros((num_solutions, num_solutions))
for i in range(num_solutions):
for j in range(i+1, num_solutions):
comparison = float(input("{}相对{}的比较重要性为:".format(indicator[i], indicator[j])))
comparison_matrix[i][j] = comparison
comparison_matrix[j][i] = 1 / comparison
return comparison_matrix
# 进行一致性检验
def consistency_check(comparison_matrix):
num_criteria = comparison_matrix.shape[0]
# 计算特征向量
eigenvalues, eigenvectors = np.linalg.eig(comparison_matrix)
max_eigenvalue = max(eigenvalues)
max_eigenvector = eigenvectors[:, np.argmax(eigenvalues)].real
# 计算一致性指标CI
consistency_index = (max_eigenvalue - num_criteria) / (num_criteria - 1)
# 计算随机一致性指标RI
random_index = {
1: 0,
2: 0,
3: 0.58,
4: 0.90,
5: 1.12,
6: 1.24,
7: 1.32,
8: 1.41,
9: 1.45,
10: 1.49,
11: 1.51,
12: 1.48,
13: 1.56,
14: 1.57,
15: 1.59
}
random_index_value = random_index.get(num_criteria)
# 计算一致性比例CR
consistency_ratio = consistency_index / random_index_value
return consistency_ratio
#主程序
# 计算指标的权重结果
num_indicators = int(input("请输入指标的数量:"))
indicators = []
for i in range(num_indicators):
indicator = input("请输入第{}个指标:".format(i+1))
indicators.append(indicator)
# 进行指标权重的比较,并计算指标的权重结果
indicator_comparison_matrix = input_comparison_matrix(indicators)
indicator_weights = calculate_weights(indicator_comparison_matrix)
#计算录入不同方案的比较矩阵
num_solutions = int(input("请输入方案的数量:"))
solutions = []
for i in range(num_solutions):
solution = input("请输入第{}个方案:".format(i+1))
solutions.append(solution)
#计算不同方案在同一指标下评估占比的权重
solution_weight_matrix = np.zeros((num_indicators, num_solutions))
solution_check_list = []
for indicator in range(num_indicators):
print("请根据{}对不同方案的重要程度进行比较:".format(indicators[indicator]))
comparison_matrix = input_comparison_matrix(solutions)
solutions_weight = calculate_weights(comparison_matrix)
solution_check = consistency_check(comparison_matrix)
solution_weight_matrix[indicator] = solutions_weight
solution_check_list.append(solution_check)
# 计算不同方案综合比较结果
scores = np.dot(indicator_weights,solution_weight_matrix)
# 进行一致性检验
indicator_check = consistency_check(indicator_comparison_matrix)
# 输出评估结果
print("指标权重结果为:")
print(indicator_weights)
print("不同指标对应方案的综合打分结果为:")
print(solution_weight_matrix)
print("方案综合评选结果为:")
print(scores)
print("指标检验和方案检验,进行一致性检验结果如下:")
print(indicator_check,solution_check_list)
输出结果参考:
请输入指标的数量:3
请输入第1个指标:指标1
请输入第2个指标:指标2
请输入第3个指标:指标3
指标1相对指标2的比较重要性为:3
指标1相对指标3的比较重要性为:2
指标2相对指标3的比较重要性为:2
请输入方案的数量:2
请输入第1个方案:方案1
请输入第2个方案:方案2
请根据指标1对不同方案的重要程度进行比较:
方案1相对方案2的比较重要性为:2
请根据指标2对不同方案的重要程度进行比较:3
请根据指标3对不同方案的重要程度进行比较:
方案1相对方案2的比较重要性为:3
指标权重结果为:
[0.54721643+0.j 0.26307422+0.j 0.18970934+0.j]
不同指标对应方案的综合打分结果为:
[[0.66666667 0.33333333]
[0.75 0.25 ]
[0.75 0.25 ]]
方案综合评选结果为:
[0.70439863+0.j 0.29560137+0.j]
指标检验和方案检验,进行一致性检验结果如下:
(-0.7451630649499623+0j) [-inf, -inf, -inf]