目录

选择

选择题总结

        特殊矩阵的压缩存储

1.对阵矩阵

2.三角矩阵

3.三对角矩阵（带状矩阵）

编程

---

选择

1.

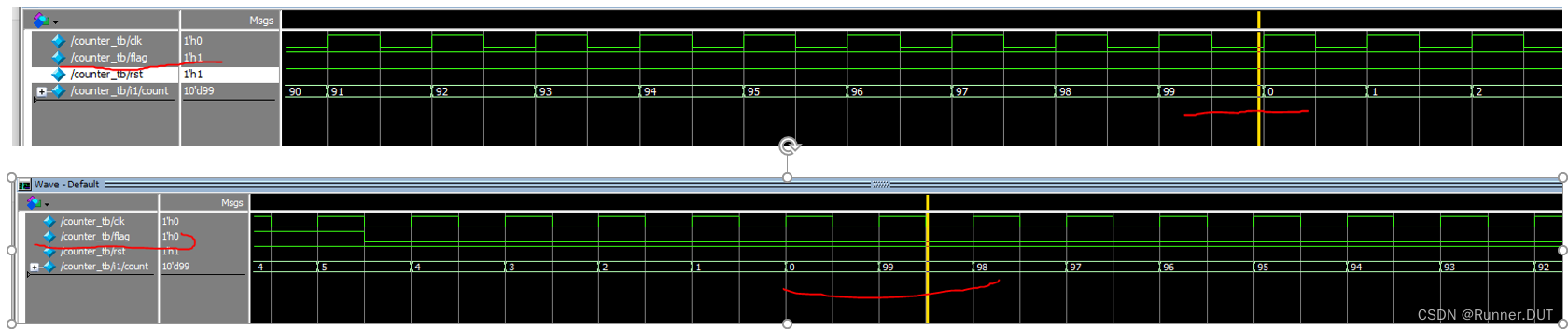
设有一个 10 阶的下三角矩阵 A （包括对角线），按照行优先的顺序存储到连续的 55 个存储单元中，每个数组元素占 1 个字节的存储空间，则 A[5][4] 地址与 A[0][0] 的地址之差为 ()

A.  10                                B.  19                              C.  28                              D.  55

 答案：B

解析：下三角矩阵A，
                        A[5][5]的地址：1+2+3+4+5+6=21
                        A[5][4]地址：21-1=20
                        A[5][4]-A[0][0]=20-1=19  //减1是因为数组下标从0开始

2.

JDK8之前版本，HashMap的数据结构是怎样的？

A.  数组                      B.  链表                        C.  数组+链表/红黑树                  D.  二叉树

答案：C

解析：HashMap在Node数组中进行哈希查找,使用链接法处理冲突,冲突较少时使用链表,目前版本当冲突的键达到8时,会把链表转换为红黑树. 

3.

将10阶对称矩阵压缩存储到一维数组A中，则数组A的长度最少为（）

A.  100                         B.  40                          C.  55                      D.  80

答案：C

解析：主对角线都存：10个，剩下的90个只存一半45个，共55个

 n(a1+an)/2  等差求和公式  10(1+10)/2 = 55

4.

定义数组char a[][3] = {1,2,3,4,5,6,7,8}，则数组a的第一维的大小是多少 ()

A.  2                      B.  3                            C.  4                       D.  无法确定

 答案：B

解析：每行只能存3个数，有8个数，所以要三行才能存完（此时有一个空位，c语言会补0），所以数组a就是三行三列。

                                        1     2     3

                                        4     5     6

                                        7     8     0

5.

设有一个10阶对称矩阵A[10][10]，采用压缩存储方式按行将矩阵中的下三角部分的元素存入一维数组B[  ]中，A[0][0]存入B[0]中，则A[8][6]在B[  ]的（    ）位置。    

A.  32                                     B.  33                          C.  42                         D.  65

答案：C

解析： 

由于是对称矩阵，因此压缩存储可以认为只要存储下三角矩阵。

(0,0)                                                           1

(1,0)(1,1)                                                    2

(2,0)(2,1) (2,2)                                           3

(3,0)(3,1) (3,2) (3,3)                                   4

(4,0)(4,1) (4,2) (4,3) (4,4)                           5

(5,0)(5,1) (5,2) (5,3) (5,4) (5,5)                   6 

(6,0)(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)          7

(7,0)(7,1) (7,2) (7,3) (7,4) (7,5) (7,6) (7,7)  8 

(8,0)(8,1) (8,2) (8,3) (8,4) (8,5) (8,6)          7

1+2+3+4+5+6+7+8+7-1=42   //减1是因为数组下标从0开始

另一种方法：

下标从i=0,j=0开始，A[8][6]实际上是第9行第7列。i=9,j=7。

计算公式为：当i>j,    i(i-1)/2+j;

                     当i<j,     j(j-1)/2+i;

选择题总结

特殊矩阵的压缩存储（对称矩阵，三角矩阵和三对角矩阵）

（均假设数组的下标从0开始）

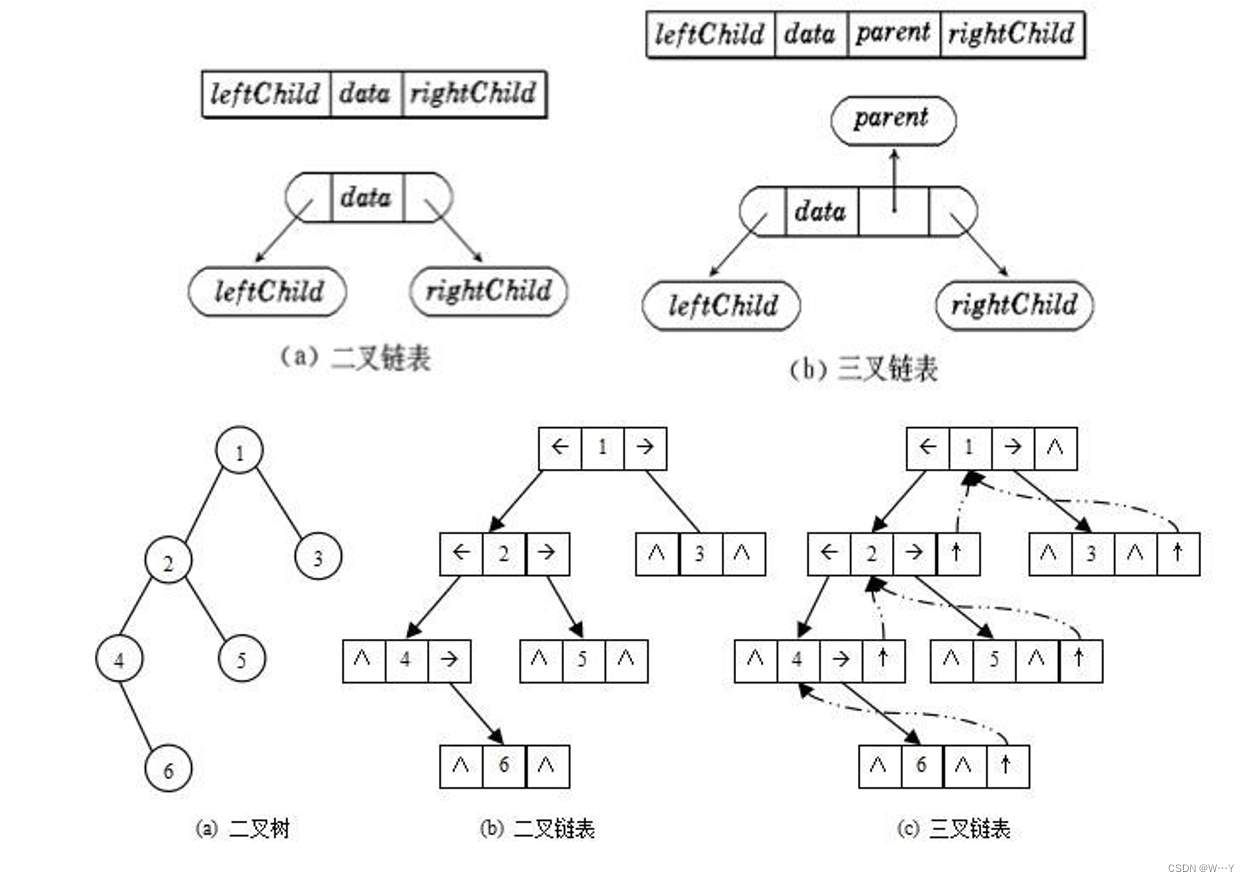
1.对阵矩阵

定义：若对一个n阶矩阵A中的任意一个元素 aᵢ,ⱼ 都有aᵢ,ⱼ=aⱼ,ᵢ （1≤i,j≤n），则称其为对称矩阵。

 存储策略：只存储主对角线＋下三角区（或主对角线+上三角区），以主对角线+下三角区为例，按照行优先把这些元素放入到一维数组中，就得到了下面的样子的一维数组：

a₁₁

a₂₁

a₂₂

a₃₁

...

aₙ,ₙ₋₂

aₙ,ₙ₋₁

aₙ,ₙ

一维数组的大小应该定义为 (1+n)*n/2, 此公式通过求和公式，将每行元素相加即可得到。

根据性质aᵢ,ⱼ=aⱼ,ᵢ可以得到矩阵所有元素与一维数组下标k的对应关系如下：

按照行优先存储原则，aᵢ,ⱼ是第几个元素？

答：因为是行优先，所以 aᵢ,ⱼ是第  1+2+...+i-1+j 个元素，即第 i*(i-1)/2+j-1个元素。

按照列优先存储原则，​​​​​​​aᵢ,ⱼ是第几个元素？

答：因为是列优先，所以先算出前 j-1 行有多少个元素，由每列元素个数与列数 j 有关，可知每列的元素个数为 n-(j-1) 个，前 j-1 行即 n-(1-1) + n-(2-1) + n-(3-1) + ··· + n-(j-1-1)个元素，化简得前  j-1行有  n+(n-1)+...+(n-j+2) 个元素。接下来再加上第 j 行的元素，也就是 ​​​​​​​aᵢ,ⱼ 所处的那一行中， 前面的元素个数，个数为 i - j 个，综上 ​​​​​​​aᵢ,ⱼ  是第 n+(n-1)+...+(n-j+2)+(i-j)+1 个元素。

2.三角矩阵

下三角矩阵的存储思想：按行优先原则将下三角区域元素（包括主对角线元素）存入一维数组中，并在最后一个位置存储常量c。 

得到一维数组：

按照行优先存储原则，​​​​​​​aᵢ,ⱼ是第几个元素？ 

上三角矩阵的存储思想：按行优先原则将上三角区域元素（包括主对角线元素）存入一维数组中，并在最后一个位置存储常量c。 一维数组和下三角矩阵的一样。

按照行优先存储原则，​​​​​​​aᵢ,ⱼ是第几个元素？ 

3.三对角矩阵（带状矩阵）

存储思想：按行优先或列优先原则，只存储带状部分。 

 矩阵中3条对角线上的元素​​​​​​​aᵢ,ⱼ在一维数组中存放的下标为k=2i+j-3

编程

题目：从顺序表中删除具有最小值的元素（假设唯一）并由函数返回被删除元素的值。空出的位置由最后一个元素填补，若顺序表为空，则显示出错信息并退出运行。 

思路：先判断表是否为空，为空则退出，不为空则搜索整个顺序表，查找最小元素并记住其位置，最后用最后一个元素填补空出的位置。 

//核心代码

bool  DelMin(Sqlist& L, Elemtype& value) {
	if (L.length == 0)
		return false;  //表空的话就退出操作
	value = L.data[0];
	int pos = 0;
	for (int i = 1;i < L.length;i++) { //循环查找最小元素并赋值给value
		if (L.data[i] < value) {
			value = L.data[i];
			pos = i;
		}
	}
	L.data[pos] = L.data[L.length - 1];//最后一个元素填补空出的位置
	L.length--;
	return true;
}