算法通关村第十九关——动态规划是怎么回事(青铜)
- 前言
- 1 什么是动态规划
- 2 动态规划的解题步骤
- 3 简单入门
- 3.1 组合总和
- 3.2 最小路径和
- 3.3 三角形最小路径和
- 4 理解动态规划
前言
动态规划是一种解决复杂问题的算法思想,它将一个大问题分解为多个相互关联的子问题,并通过递推关系将子问题的解整合起来,最终得到原问题的解。动态规划的核心思想是将问题划分为重叠子问题,并存储子问题的解,避免重复计算。
动态规划通常用于求解最优化问题,如求解最长公共子序列、最短路径、背包问题等。它的基本步骤包括定义状态、设置初始状态、确定状态转移方程和计算最优解。
动态规划的优点是减少了重复计算,提高了算法效率,但它也需要额外的空间来存储子问题的解,因此在使用动态规划时需要权衡时间和空间的开销。
1 什么是动态规划
动态规划(Dynamic Programming),简称dp,是一种解决多阶段决策问题的优化方法。它通过将问题划分为多个子问题,并保存子问题的解,以避免重复计算,从而得到原问题的最优解。
动态规划的核心思想是利用子问题的最优解来推导出原问题的最优解。具体来说,动态规划通常包含以下步骤:
- 定义状态:将原问题划分为若干个子问题,并确定每个子问题的状态,即问题的不同维度。
- 设置初始状态:初始化边界条件和初始状态值。
- 确定状态转移方程:根据子问题之间的关系,建立状态之间的递推关系,即通过已解决的子问题来求解当前问题。
- 计算最优解:按照状态转移方程,从初始状态逐步计算出最终的目标状态,即原问题的最优解。
下面以求解斐波那契数列为例进行详细说明。
斐波那契数列的定义为:F(n) = F(n-1) + F(n-2),其中F(0) = 0,F(1) = 1。
使用动态规划求解斐波那契数列的步骤如下:
- 定义状态:将斐波那契数列的第n个数记为F(n),即问题的状态为n。
- 设置初始状态:定义F(0) = 0和F(1) = 1,作为初始状态。
- 确定状态转移方程:根据斐波那契数列的递推关系式F(n) = F(n-1) + F(n-2),可以得到状态转移方程F(n) = F(n-1) + F(n-2)。
- 计算最优解:按照状态转移方程从初始状态开始逐步计算出F(n)的值,直到计算出F(n)。
代码如下:
public class Fibonacci {
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
// 定义一个数组来保存斐波那契数列的每个元素的值
int[] dp = new int[n + 1];
// 设置初始状态
dp[0] = 0;
dp[1] = 1;
// 确定状态转移方程,计算最优解
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
// 返回结果
return dp[n];
}
public static void main(String[] args) {
int n = 10;
System.out.println("Fibonacci(" + n + ") = " + fibonacci(n));
}
}
在上面的代码中,我添加了注释来说明使用动态规划解决斐波那契数列的步骤。
- 首先定义了一个数组
dp用于保存斐波那契数列的每个元素的值。 - 然后,设置初始状态,即
dp[0] = 0和dp[1] = 1。 - 接下来,通过一个循环从第3个元素开始计算每个元素的值,并使用状态转移方程
dp[i] = dp[i - 1] + dp[i - 2]来计算最优解。 - 最后,返回数组中索引为
n的元素值,即得到斐波那契数列的第n个数。
执行上述代码,可以得到输出结果为Fibonacci(10) = 55,表示斐波那契数列的第10个数为55.
与动态规划相对应的是贪心算法(Greedy Algorithm)。
贪心算法每次选择当前状态下的最优解,而不考虑全局最优解。贪心算法通常适用于满足贪心选择性质和最优子结构性质的问题,但不一定能得到全局最优解。
举个例子:
假设有一笔钱要找零,在某个国家的货币单位只有1元、5元和10元。目标是找零的总数量最少。
-
使用贪心算法来解决这个问题时,每次都选择面额最大的币种进行找零。例如,要找零27元,先选择10元,剩下17元,再选择10元,剩下7元,最后选择5元和两个1元,得到找零总数量为4。
-
然而,贪心算法在某些情况下并不一定能得到最优解。对于要找零15元的情况,贪心算法会选择10元和5个1元,共计6个硬币。而实际上,最优解是使用三个5元的硬币,共计3个硬币。
因此,动态规划可以得到全局最优解,而贪心算法只能得到局部最优解。
2 动态规划的解题步骤
以下内容摘抄于代码随想录:代码随想录——动态规划
当解动态规划问题时,许多同学常常会陷入一个误区,认为将状态转移公式背下来,稍加修改就可以开始编写代码了。甚至有些同学在通过测试之后,仍不清楚dp[i]所代表的是什么。
这种模糊的状态会使我们对问题的本质理解不清,因此在遇到更复杂的问题时可能就束手无策了。结果往往是去看题解,然后继续模仿而陷入这种恶性循环中。
虽然递推公式(状态转移公式)非常重要,但动态规划不仅仅只包含递推公式。
为了真正掌握动态规划,我们需要将解题过程拆解为以下五个步骤,并确保每个步骤都清晰明了!
- 确定dp数组(dp table)及其下标的含义
- 确定递推公式
- 初始化dp数组
- 确定遍历顺序
- 举例推导dp数组
可能有些同学会想,为什么要先确定递推公式,然后再考虑初始化呢?
因为在某些情况下,递推公式决定了dp数组应该如何初始化!
接下来的讲解都是以这五个步骤为基础进行的。
刷过动态规划题目的同学可能已经意识到了递推公式的重要性,觉得一旦确定了递推公式,问题就解决了。
然而,确定递推公式只是解题过程中的一小部分!
有些同学虽然知道递推公式,但却不清楚dp数组该如何初始化,或者无法找到正确的遍历顺序。结果就是他们能记住公式,但无论如何修改代码都无法通过测试。
后续的讲解将逐渐展示这五个步骤的重要性。
3 简单入门
下面会通过一些例子一步步了解DP,循序渐进~
3.1 组合总和
leetcode 62. 不同路径
- 确定dp数组(dp table)以及下标的含义
dp[ i ] [ j ] :表示从(0 ,0)出发,到(i, j) 有dp[ i ] [ j ] 条不同的路径。
- 确定递推公式
想要求dp[ i ] [ j ] ,只能有两个方向来推导出来,即dp[ i -1 ] [ j ] 和 dp[ i ] [ j-1 ] 。
此时在回顾一下 dp[ i-1 ] [ j ] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[ i ] [ j-1 ] 同理。
为什么呢?
当我们想要求解dp[ i ] [ j ] ,时,只有两个方向可以推导出它的值,即dp[ i-1 ] [ j ] ,和dp[ i ] [ j-1 ] 。这是因为在问题中机器人只能向下或向右移动。
假设我们要求dp[ i ] [ j ] ,那么根据题目的限制条件,有以下两种情况:
- 从上方的位置dp[ i -1] [ j ] 向下移动一步,到达位置dp[ i ] [ j ] 。
- 从左边的位置dp[ i ] [ j-1 ] 向右移动一步,到达位置dp[ i ] [ j ] 。
因此,我们可以通过这两个方向的状态值来推导出dp[ i ] [ j ] 的值,即dp[ i ] [ j ] ,= dp[ i -1 ] [ j ] + dp[ i ] [ j -1 ] ,。
通过不断迭代计算每个位置的路径数量,最终就能得到起点到终点的总路径数量。
- dp数组的初始化
如何初始化呢,首先dp[ i ] [ 0 ] 一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[ 0] [ j ] 也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序
这里要看一下递推公式dp[ i ] [ j ] = dp[ i-1 ] [ j ] + dp[ i ] [ j-1 ] ,dp[ i ] [ j ] 都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[ i ] [ j ] 的时候,dp[ i -1 ] [ j ] 和 dp[ i ] [ j-1 ] 一定是有数值的。
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
- 距离推导dp数组
如图所示:
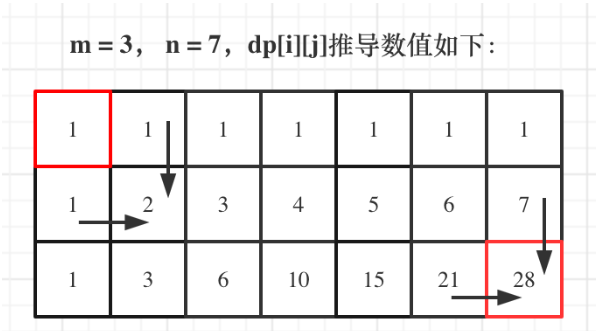
最后代码如下:
class Solution {
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
//初始化
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
}
3.2 最小路径和
leetcode 64. 最小路径和
思路:
这道题要一步步去理解,因为刚刚入门,所以需要逐渐理解整个思路,尤其是dp数组的定义,特别重要!!
下面使用5步法来解决:
- 确定dp数组(dp table)及其下标的含义
在这道题中,我们要求从起点到达位置(i,j)的最小路径和。
因此,dp[ i ] [ j ]表示从起点到达位置(i,j)的最小路径和。
int[][] dp = new int[i][j];
- 确定递推公式
根据题目要求,我们可以向右或向下移动,
所以到达位置(i,j)的最小路径和等于上方和左方路径和的较小值加上当前位置的数字,
即dp[ i ] [ j ] = min(dp[ i-1 ] [ j ], dp[ i ] [ j-1 ] ) + grid [ i ] [ j ] 。
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
- 初始化dp数组
由于题目要求找出最小路径和,我们可以将dp数组全部初始化为一个较大的值(比如MAX_VALUE),
除了dp [ 0 ] [ 0 ] 应该等于grid [ 0 ] [ 0 ] ,因为到达起点的最小路径和就是起点的数字本身。
dp[0][0] = grid[0][0];
- 确定遍历顺序
题目要求从左上角开始,先遍历行再遍历列。
这是因为在计算dp[i] [j]时,我们需要用到dp[i-1] [j]和dp[i] [j-1]的值,而这两个值都是在当前行或当前列的前面位置计算得出的。所以我们要按照从上到下、从左到右的顺序进行遍历。
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
}
}
- 举例推导dp数组
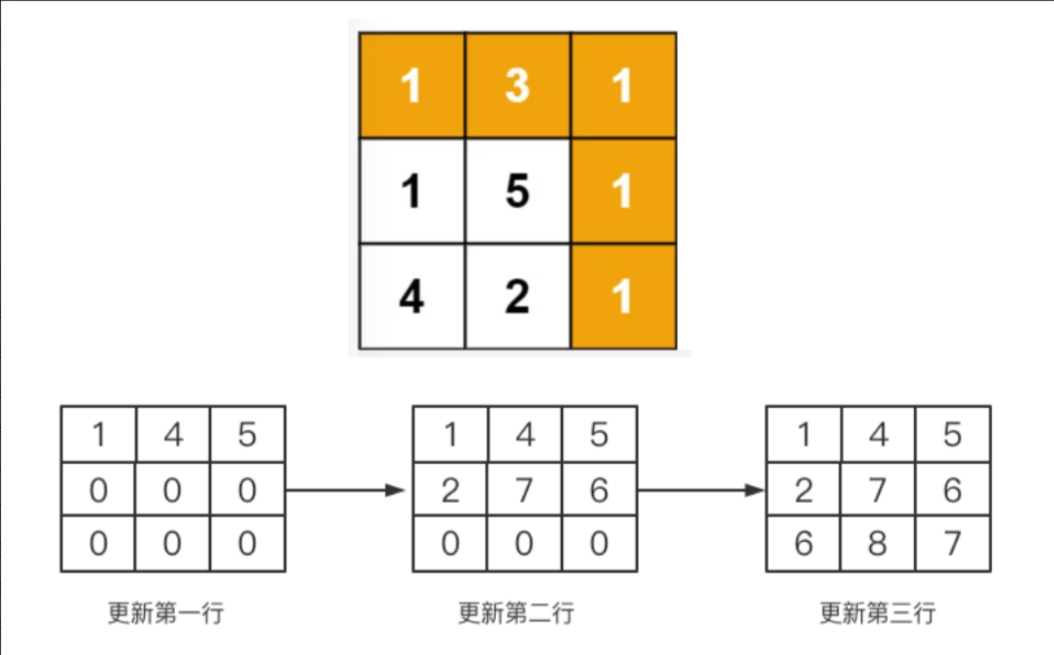
最后代码如下:
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
// 1. 确定dp数组及其下标的含义
int[][] dp = new int[m][n];
// 2. 递推公式:dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
// 3. 初始化dp数组
dp[0][0] = grid[0][0];
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i-1][0] + grid[i][0];
}
for (int j = 1; j < n; j++) {
dp[0][j] = dp[0][j-1] + grid[0][j];
}
// 4. 确定遍历顺序
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
// 5. 举例推导dp数组
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
}
}
return dp[m-1][n-1]; // 最后结果即为dp数组右下角的值
}
}
3.3 三角形最小路径和
leetcode 120. 三角形最小路径和
这道题跟上一题很像,也是计算路径和,所以整体思路是一样的
老样子,使用五步法:
- 确定dp数组(dp table)及其下标的含义:
dp[i] [j] 表示到达第 i 行第 j 列的最小路径和。
int m = triangle.size();
int[][] dp = new int[m][m];
- 确定递推公式:
-
dp[i] [j] = dp[i-1] [j] + triangle[i] [j] (当 j=0时,只能从上一行的第一个元素向下走)
-
dp[i] [j] = dp[i-1] [j-1] + triangle[i] [j] (当 j=i 时,只能从上一行的最后一个元素向下走)
-
dp[i] [j] = min(dp[i-1] [j], dp[i-1] [j-1]) + triangle[i] [j] (其他情况)
- 初始化dp数组:
没啥好说的,初始化的就是第一个数
dp[0][0] = triangle.get(0).get(0);
- 确定遍历顺序:
从上到下依次遍历每一行,从左到右依次遍历每一列。
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);
for (int j = 1; j < i; j++) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);
}
dp[i][i] = dp[i-1][i-1] + triangle.get(i).get(i);
}
- 举例推导dp数组
这一步是验证,也是为了防止错误
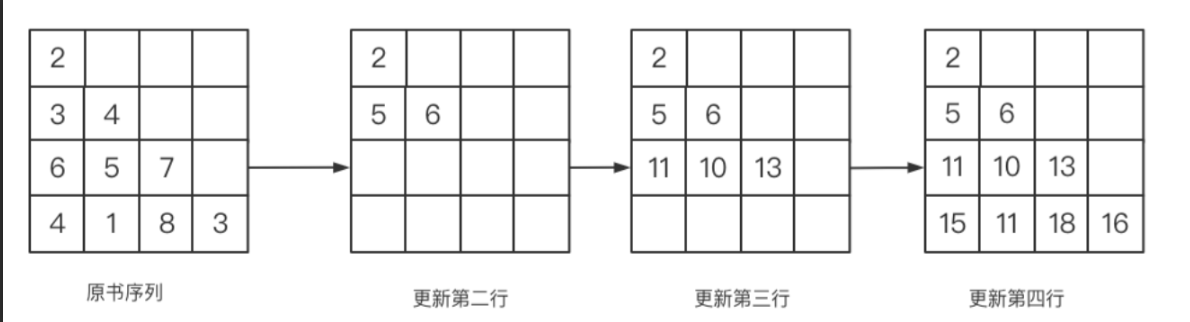
全代码如下:
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int m = triangle.size();
int[][] dp = new int[m][m];
dp[0][0] = triangle.get(0).get(0);
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);
for (int j = 1; j < i; j++) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);
}
dp[i][i] = dp[i-1][i-1] + triangle.get(i).get(i);
}
int min = dp[m - 1][0];
for (int i = 1; i < m; i++) {
min = Math.min(min, dp[m - 1][i]);
}
return min;
}
}
4 理解动态规划
做了前面三道题,也能感觉到动态规划与回溯的一些不一样地方,虽然都有模版可以使用
动态规划(Dynamic Programming)是一种解决问题的算法思想,它将一个待求解的问题分解成若干个子问题,并先求解这些子问题,再从中得到原问题的解。动态规划可以高效地解决一些需要穷举所有可能情况的问题。
重点:
区分动态规划和回溯的重要区别在于动态规划只关心当前结果是什么,而不关心怎么来的,因此无法获得完整的路径。而回溯可以记录所有的路径,但解决效率较低。
动态规划的基本思想是通过穷举来找到满足要求的最优解,并使用记忆化搜索来消除重复计算。记忆化搜索将已经计算过的结果存储在数组中,避免重复计算。
动态规划问题具备最优子结构,即问题的最优解可以由其子问题的最优解递推得到。为了能正确地穷举子问题并得到最优解,需要编写正确的状态转移方程。大部分状态转移可以通过数组实现,因此动态规划代码一般以for循环为主体。
以下是一个典型的动态规划代码模板:
int dp[] = new int[n]; // 创建一个数组用于存储子问题的解
dp[0] = base case; // 设置初始状态
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
dp[i] = 计算dp[i]和dp[j]之间的关系; // 根据状态转移方程计算当前子问题的解
}
}
return 最终结果;
要注意的是,动态规划问题的难点在于找到最优子结构和编写正确的状态转移方程。具体问题的最优子结构和状态转移方程需要根据实际情况进行分析。