前言

想要精通算法和SQL的成长之路 - 系列导航

一. 课程表II （拓扑排序）

原题链接
在这里插入图片描述

1.1 拓扑排序

核心知识：

拓扑排序是专门应用于有向图的算法。
BFS的写法就叫拓扑排序，核心就是：让入度为0的节点入队。
拓扑排序的结果不唯一。
同时拓扑排序有一个重要的功能：能够检测有向图中是否存在环。

我们先分析一下本题：

先说下课程，课程有它自己的一个先后的依赖顺序。符合 “有向” 。
想要学习某个课程，它的前缀课程可能有多个。那么我们可以用 “度” 的概念去标识衡量。这里是入度。

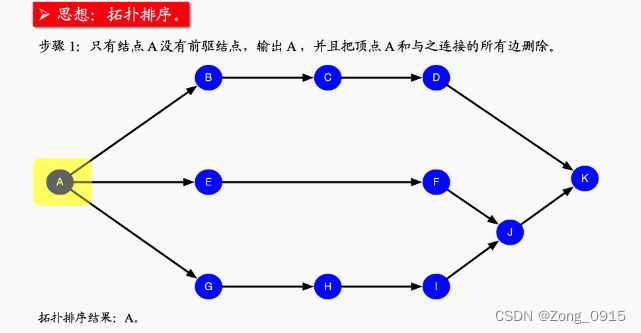
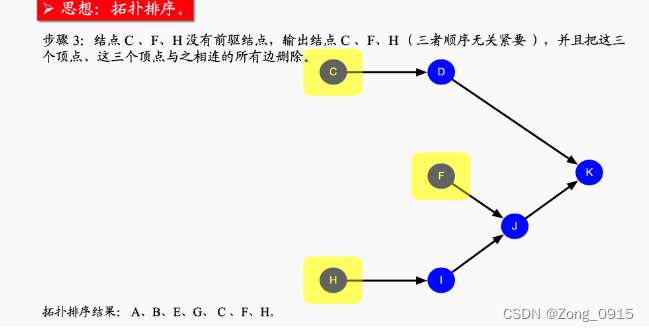
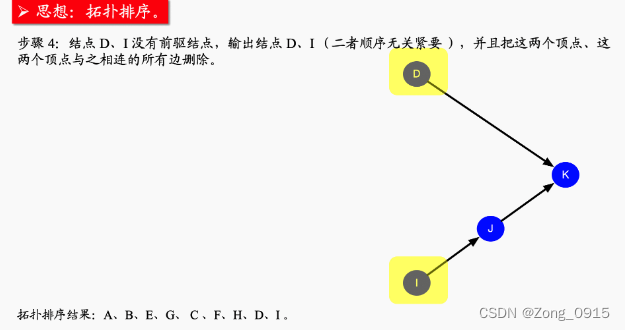
先用图来解释下本次算法的核心方向（摘自leetcode题解）：

说白了就是：

不断地找入度为0的节点，然后剔除。剔除的同时维护后续节点的入度数。
以此类推。

1.2 题解

那么本题我们该如何解？我们一步步来，我们以numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]] 为例来说。官方解释：

总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。

public int[] findOrder(int numCourses, int[][] prerequisites) {

}

那么我们可以知道这个二维数组prerequisites中，第二个数字代表：”前缀“，第一个数字代表：”后缀“。[1,0] 用图表示就是：0->1。同时我们还可以计算出，此时1这个节点的入度应该+1。因为0指向了1。

1.首先，我们要对入参做一个校验：

// 1. 先判断数组或者numCourses为空的情况
if (numCourses <= 0) {
    return new int[0];
}

2.我们需要遍历二维数组prerequisites中，拿到所有节点的入度以及这个拓扑图的结构。

我们用inDegree[]数组表示各个节点的入度。
用一个HashSet数组表示邻接表的结果。数组的索引代表的是节点的值。数组值（即HashMap）代表这个节点的所有后继节点。以0为例，它的后继节点有1和2。

// 2. 用inDegree[] 数组表示每个节点的入度数。
// 同时维护拓扑图的结构例如：0->1，0->2
HashSet<Integer>[] adj = new HashSet[numCourses];
// 初始化下
for (int i = 0; i < numCourses; i++) {
    adj[i] = new HashSet<>();
}
// 构建入度
int[] inDegree = new int[numCourses];
for (int[] p : prerequisites) {
    // 入度+1
    inDegree[p[0]]++;
    // 把当前节点的后继节点存储起来
    adj[p[1]].add(p[0]);
}

3.我们用一个队列，用来存储入度为0的节点。

// 3.准备个队列,存储入度为0的节点
LinkedList<Integer> queue = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
    if (inDegree[i] == 0) {
        queue.offer(i);
    }
}

为啥要这一个步骤？如果发现没有入度为0的节点，说明啥，成环了，那本题就无解。如图：
在这里插入图片描述
4.如果存在入度为0的节点，我们开始往后递归，做2.1节的内容。

先拿到入度为0的节点，删除它（把他放入结果集）。
同时维护后继节点的入度。
如果后继节点入度数-1后，为0。那么同样放入到队列中递归。

// 结果集
int[] res = new int[numCourses];
// 统计结果集中的个数
int count = 0;
while (!queue.isEmpty()) {
    // 入度为0的节点，我们弹出
    Integer head = queue.poll();
    // 放入结果集
    res[count++] = head;
    // 当前入度为0节点对应的后继节点。如果是0 --> 1,2
    HashSet<Integer> nextNodeList = adj[head];
    // 更新后继节点的入度
    for (Integer nextNode : nextNodeList) {
        // 对应的后继节点的入度要减1，
        inDegree[nextNode]--;
        // 如果入度-1后，为0了。再入队
        if (inDegree[nextNode] == 0) {
            queue.offer(nextNode);
        }
    }
}

最后，我们只需要关心结果集个数是否和题干中的numCourses一致。一致的话返回我们构建的结果集，否则本题为空解：

// 如果遍历完了，发现count数量和 numCourses一致，说明有一个正确的结果集
if (count == numCourses) {
    return res;
}
return new int[0];

最终完整代码如下：

public class Test210 {
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        // 1. 先判断数组或者numCourses为空的情况
        if (numCourses <= 0) {
            return new int[0];
        }
        // 2. 用inDegree[] 数组表示每个节点的入度数。
        // 同时维护拓扑图的结构例如：0->1，0->2
        HashSet<Integer>[] adj = new HashSet[numCourses];
        // 初始化下
        for (int i = 0; i < numCourses; i++) {
            adj[i] = new HashSet<>();
        }
        // 构建入度
        int[] inDegree = new int[numCourses];
        for (int[] p : prerequisites) {
            // 入度+1
            inDegree[p[0]]++;
            // 把当前节点的后继节点存储起来
            adj[p[1]].add(p[0]);
        }
        // 3.准备个队列,存储入度为0的节点
        LinkedList<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }
        // 结果集
        int[] res = new int[numCourses];
        // 统计结果集中的个数
        int count = 0;
        while (!queue.isEmpty()) {
            // 入度为0的节点，我们弹出
            Integer head = queue.poll();
            // 放入结果集
            res[count++] = head;
            // 当前入度为0节点对应的后继节点。如果是0 -- > 1,2
            HashSet<Integer> nextNodeList = adj[head];
            // 更新后继节点的入度
            for (Integer nextNode : nextNodeList) {
                // 对应的next节点的入度要减1，
                inDegree[nextNode]--;
                // 如果入度-1后，为0了。再入队
                if (inDegree[nextNode] == 0) {
                    queue.offer(nextNode);
                }
            }
        }
        // 如果遍历完了，发现count数量和 numCourses一致，说明有一个正确的结果集
        if (count == numCourses) {
            return res;
        }
        return new int[0];
    }
}