【AIOT】Python语音处理

语音信号有三个重要的参数：声道数、取样频率和量化位数。

声道数：可以是单声道或者是双声道
采样频率：一秒内对声音信号的采集次数，44100Hz采样频率意味着每秒钟信号被分解成44100份。换句话说，每隔144100秒就会存储一次，如果采样率高，那么媒体播放音频时会感觉信号是连续的。
量化位数：用多少bit表达一次采样所采集的数据，通常有8bit、16bit、24bit和32bit等几种

1. 文件读写

2. 信号处理

语音信号是一个非平稳的时变信号，但语音信号是由声门的激励脉冲通过声道形成的，而声道(人的口腔、鼻腔)的肌肉运动是缓慢的，所以“短时间”(10~30ms)内可以认为语音信号是平稳时不变的。由此构成了语音信号的“短时分析技术”。在短时分析中，将语音信号分为一段一段的语音帧，每一帧一般取10~30ms，我们的研究就建立在每一帧的语音特征分析上。提取的不同的语音特征参数对应着不同的语音信号分析方法：时域分析、频域分析、倒谱域分析…由于语音信号最重要的感知特性反映在功率谱上，而相位变化只起到很小的作用，所有语音频域分析更加重要。

2.0. 预加重

所谓预加重是指在信号发送之前，先对模拟信号的高频部分进行适当的提升，在接收到信号之后，进行逆处理，即去加重。预加重和去加重技术可以使信号在传输中高频损耗的影响降低，也可以是噪声的频谱发生变化，这是模拟降噪的原理。声道的终端是口和唇，口唇辐射对低频影响比较小，但是对高频段影响比较大，欲加重技术技术为了提升高频分辨率，欲加重的传递函数是 $H(z)=1−aZ^{-1}$ 。

2.1. 信号窗

通常对信号截断、分帧需要加窗，因为截断都有频域能量泄露，而窗函数可以减少截断带来的影响。时域加窗会导致主瓣变宽而旁瓣得到明显降低，并且最大幅值也有所降低。

傅里叶变换后主要的特征有频率、幅值和相位，加窗对相位的影响是线性的，所以一般不用考虑。
加窗对频率和幅值的影响是关联的，对于时域的单个频率信号，加窗之后的频谱就是将窗谱的谱峰位置平移到信号的频率处，然后进行垂直缩放。说明加窗的影响取决于窗的功率谱，也就容易理解为什么总常看到对窗特征主瓣、旁瓣等的描述。
主瓣变宽就可能与附近的频率的谱相叠加，意味着更难找到叠加后功率谱中最大的频率点，即降低了频率分辨率，较难定位中心频率。旁瓣多意味着信号功率泄露多，主瓣被削弱了，即幅值精度降低了。

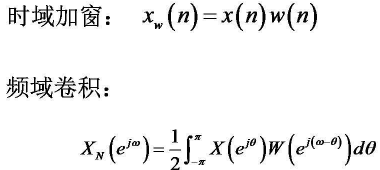
通常时域上加窗更为普遍，时域截断效应带来了频谱的泄漏，窗函数是为了减小这个截断效应，被设计成一组加权系数w(n)。域加窗在时域上表现的是点乘，因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程，相当于一组具有特定函数形状的滤波器，因此，原始信号中在某一频率点上的能量会结合滤波器的形状表现出来，从而减小泄漏。

对线性调频信号(LFM)的时域加窗会导致主瓣变宽而旁瓣得到明显降低，并且最大幅值也有所降低

时域加窗

频率加窗

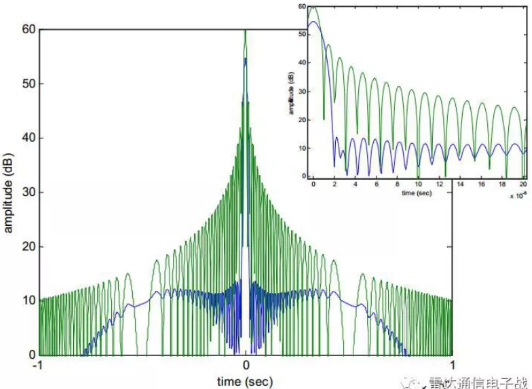
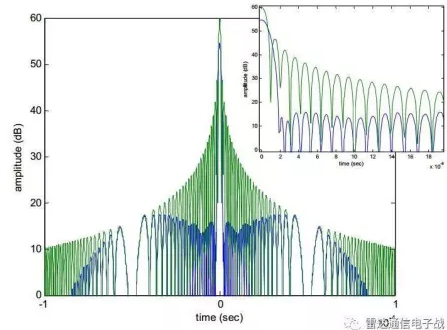
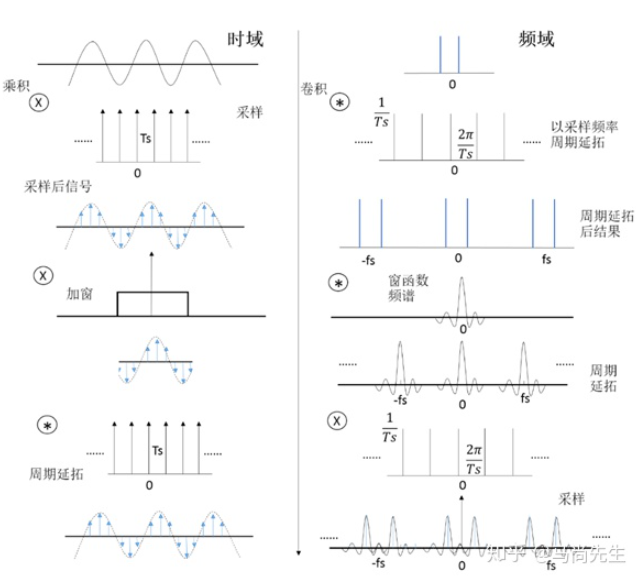
如果仅要求精确读出主瓣频率，而不考虑幅值精度，则可选用主瓣宽度比较窄而便于分辨的矩形窗，例如测量物体的自振频率等；如果分析窄带信号，且有较强的干扰噪声，则应选用旁瓣幅度小的窗函数，如汉宁窗、三角窗等；对于随时间按指数衰减的函数，可采用指数窗来提高信噪比。

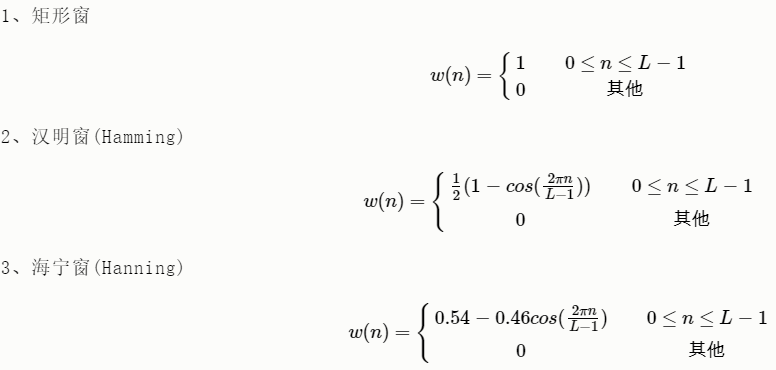
2.2. 信号分帧

在分帧中，相邻两帧之间会有一部分重叠，帧长(wlen) = 重叠(overlap)+帧移(inc)，如果相邻两帧之间不重叠，那么由于窗函数的形状，截取到的语音帧边缘会出现损失，所以要设置重叠部分。inc为帧移，表示后一帧第前一帧的偏移量，fs表示采样率，fn表示一段语音信号的分帧数。

#没有加窗的语音分帧
import numpy as np
import wave
import os
#import math
 
def enframe(signal, nw, inc):
    '''将音频信号转化为帧。
    参数含义：
    signal:原始音频型号
    nw:每一帧的长度(这里指采样点的长度，即采样频率乘以时间间隔)
    inc:相邻帧的间隔（同上定义）
    '''
    signal_length=len(signal) #信号总长度
    if signal_length<=nw: #若信号长度小于一个帧的长度，则帧数定义为1
        nf=1
    else: #否则，计算帧的总长度
        nf=int(np.ceil((1.0*signal_length-nw+inc)/inc))
    pad_length=int((nf-1)*inc+nw) #所有帧加起来总的铺平后的长度
    zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补，类似于FFT中的扩充数组操作
    pad_signal=np.concatenate((signal,zeros)) #填补后的信号记为pad_signal
    indices=np.tile(np.arange(0,nw),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(nw,1)).T  #相当于对所有帧的时间点进行抽取，得到nf*nw长度的矩阵
    indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
    frames=pad_signal[indices] #得到帧信号
#    win=np.tile(winfunc(nw),(nf,1))  #window窗函数，这里默认取1
#    return frames*win   #返回帧信号矩阵
    return frames
def wavread(filename):
    f = wave.open(filename,'rb')
    params = f.getparams()
    nchannels, sampwidth, framerate, nframes = params[:4]
    strData = f.readframes(nframes)#读取音频，字符串格式
    waveData = np.fromstring(strData,dtype=np.int16)#将字符串转化为int
    f.close()
    waveData = waveData*1.0/(max(abs(waveData)))#wave幅值归一化
    waveData = np.reshape(waveData,[nframes,nchannels]).T
    return waveData
 
filepath = "./data/" #添加路径
dirname= os.listdir(filepath) #得到文件夹下的所有文件名称 
filename = filepath+dirname[0]
data = wavread(filename)
nw = 512
inc = 128
Frame = enframe(data[0], nw, inc) 
#加窗的语音分帧
def enframe(signal, nw, inc, winfunc):
    '''将音频信号转化为帧。
    参数含义：
    signal:原始音频型号
    nw:每一帧的长度(这里指采样点的长度，即采样频率乘以时间间隔)
    inc:相邻帧的间隔（同上定义）
    '''
    signal_length=len(signal) #信号总长度
    if signal_length<=nw: #若信号长度小于一个帧的长度，则帧数定义为1
        nf=1
    else: #否则，计算帧的总长度
        nf=int(np.ceil((1.0*signal_length-nw+inc)/inc))
    pad_length=int((nf-1)*inc+nw) #所有帧加起来总的铺平后的长度
    zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补，类似于FFT中的扩充数组操作
    pad_signal=np.concatenate((signal,zeros)) #填补后的信号记为pad_signal
    indices=np.tile(np.arange(0,nw),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(nw,1)).T  #相当于对所有帧的时间点进行抽取，得到nf*nw长度的矩阵
    indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
    frames=pad_signal[indices] #得到帧信号
    win=np.tile(winfunc,(nf,1))  #window窗函数，这里默认取1
    return frames*win   #返回帧信号矩阵

2.3. 短时时域处理

短时能量和短时平均幅度
- 区分浊音和清音段，因为浊音的短时能量E(i)比清音大很多；
- 区分声母和韵母的分界和无话段和有话段的分界
短时平均过零率
- 可以从背景噪声中找出语音信号
- 可以用于判断寂静无话段与有话段的起点和终止位置。
- 在背景噪声较小的时候，用平均能量识别较为有效，在背景噪声较大的时候，用短时平均过零率识别较为有效。
短时自相关函数:
- 主要应用于端点检测和基音的提取，在韵母基因频率整数倍处将出现峰值特性，通常根据除R(0)外的第一峰值来估计基音，而在声母的短时自相关函数中看不到明显的峰值。
短时平均幅度差函数:
- 用于检测基音周期，而且在计算上比短时自相关函数更加简单。

2.3.0. 傅里叶变换

frequency bin: 频点采用相等的间隔，这间隔通常frequency bin（频率窗口）或FFT bin表示。

import matplotlib.pyplot as plt 
import numpy as np
import numpy.fft as fft

plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示符号

Fs = 1000;            # 采样频率
T = 1/Fs;             # 采样周期
L = 1000;             # 信号长度
t = [i*T for i in range(L)]
t = np.array(t)

S = 0.2+0.7*np.cos(2*np.pi*50*t+20/180*np.pi) + 0.2*np.cos(2*np.pi*100*t+70/180*np.pi) ;
#经过快速傅里叶变换得到一个复数数组，复数的模代表的是振幅，复数的辐角代表初相位
complex_array = fft.fft(S)
print(complex_array.shape)  # (1000,) 
print(complex_array.dtype)  # complex128 
print(complex_array[1])  # (-2.360174309695419e-14+2.3825789764340993e-13j)

#################################
plt.subplot(311)
plt.grid(linestyle=':')
plt.plot(1000*t[1:51], S[1:51], label='S')  # y是1000个相加后的正弦序列
plt.xlabel("t（毫秒）")
plt.ylabel("S(t)幅值")
plt.title("叠加信号图")
plt.legend()

###################################
plt.subplot(312)
#复数数组 经过逆向傅里叶变换得到合成的函数值数组
S_ifft = fft.ifft(complex_array)
# S_new是ifft变换后的序列
plt.plot(1000*t[1:51], S_ifft[1:51], label='S_ifft', color='orangered')
plt.xlabel("t（毫秒）")
plt.ylabel("S_ifft(t)幅值")
plt.title("ifft变换图")
plt.grid(linestyle=':')
plt.legend()

###################################
# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0])
# 复数的模为信号的振幅（能量大小）
pows = np.abs(complex_array)

plt.subplot(313)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 功率')
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs > 0], pows[freqs > 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
plt.show()

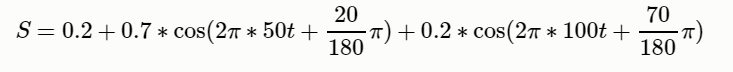
mel频率倒谱系数(MFCC)，线性预测系数(LPC)，线性预测倒谱系数(LPCC)，线谱频率(LSF)，离散小波变换(DWT)，感知线性预测(PLP)

2.3.1. 短时傅里叶变换

#绘制语音信号的频谱图
import numpy as np
from scipy.io import wavfile
import matplotlib.pyplot as plt

sampling_freq, audio = wavfile.read(r"C:\Windows\media\Windows Background.wav")   # 读取文件

audio = audio / np.max(audio)   # 归一化，标准化

# 应用傅里叶变换
fft_signal = np.fft.fft(audio)
print(fft_signal)
# [-0.04022912+0.j         -0.04068997-0.00052721j -0.03933007-0.00448355j
#  ... -0.03947908+0.00298096j -0.03933007+0.00448355j -0.04068997+0.00052721j]

fft_signal = abs(fft_signal)
print(fft_signal)
# [0.04022912 0.04069339 0.0395848  ... 0.08001755 0.09203427 0.12889393]

# 建立时间轴
Freq = np.arange(0, len(fft_signal))

# 绘制语音信号的
plt.figure()
plt.plot(Freq, fft_signal, color='blue')
plt.xlabel('Freq (in kHz)')
plt.ylabel('Amplitude')
plt.show()

def wav_to_frame(wave_data, win_len, win_shift):
    """
    进行分帧操作
    :param wave_data: 原始的数据
    :param win_len: 滑动窗长
    :param win_shift: 滑动间隔
    :return: 分帧之后的结果，输出一个帧矩阵
    """
    num_frames = (len(wave_data) - win_len) // win_shift + 1
    results = []
    for i in range(num_frames):
        results.append(wave_data[i*win_shift:i*win_shift + win_len])
    return np.array(results)

def spectrum_power(frames, NFFT):
    """
    计算每一帧傅立叶变换以后的功率谱
    参数说明：
    frames:audio2frame函数计算出来的帧矩阵
    NFFT:FFT的大小
    """
    # 功率谱等于每一点的幅度平方/NFFT
    return 1.0/NFFT * np.square(spectrum_magnitude(frames, NFFT))

def spectrum_magnitude(frames, NFFT):
    """计算每一帧经过FFT变幻以后的频谱的幅度，若frames的大小为N*L,则返回矩阵的大小为N*NFFT
    参数：
    frames:即audio2frame函数中的返回值矩阵，帧矩阵
    NFFT:FFT变换的数组大小,如果帧长度小于NFFT，则帧的其余部分用0填充铺满
    """
    complex_spectrum = np.fft.rfft(frames, NFFT)    # 对frames进行FFT变换
    # 返回频谱的幅度值
    return np.absolute(complex_spectrum)

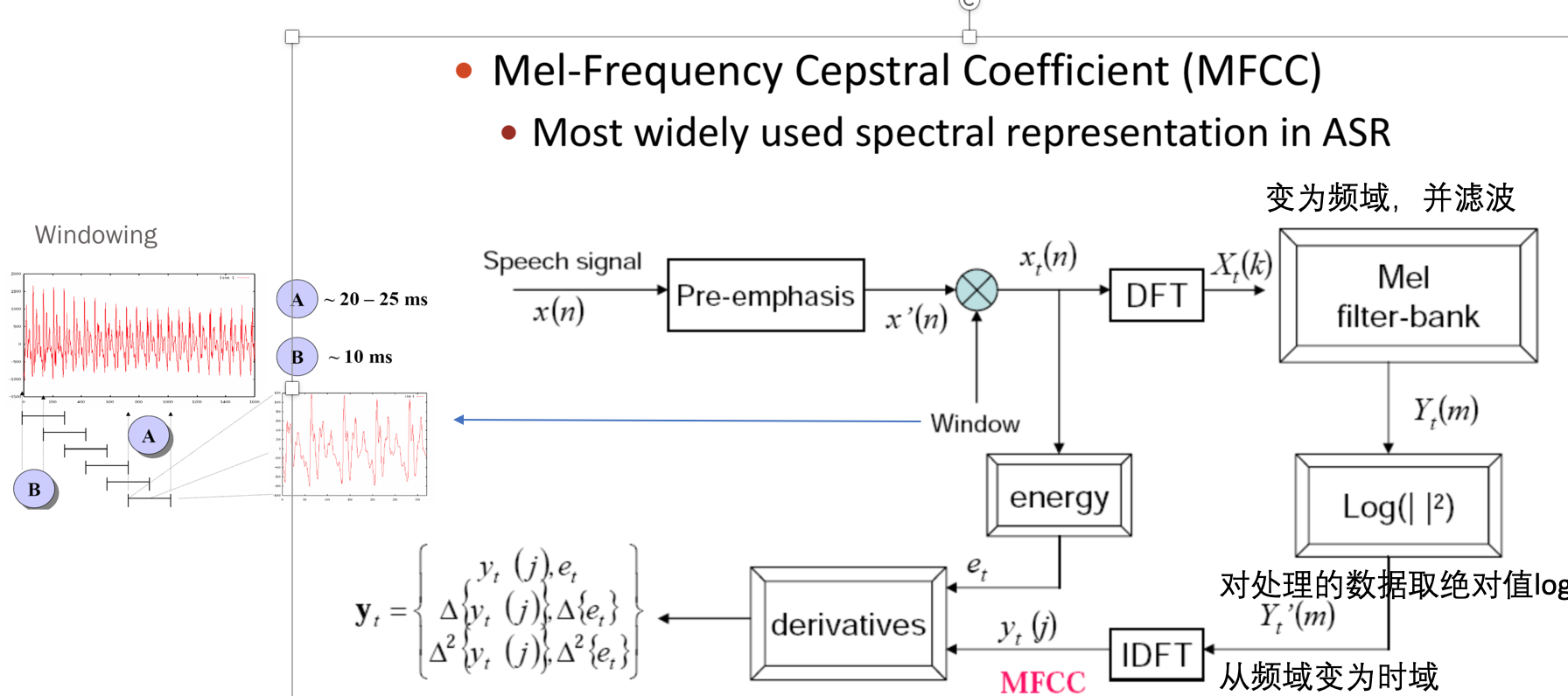
2.3.2 梅尔频率倒谱系数

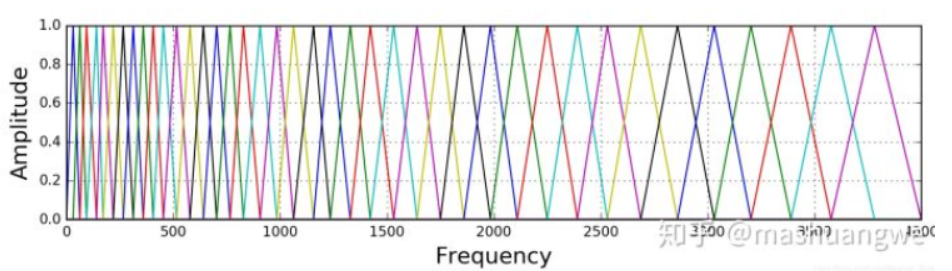
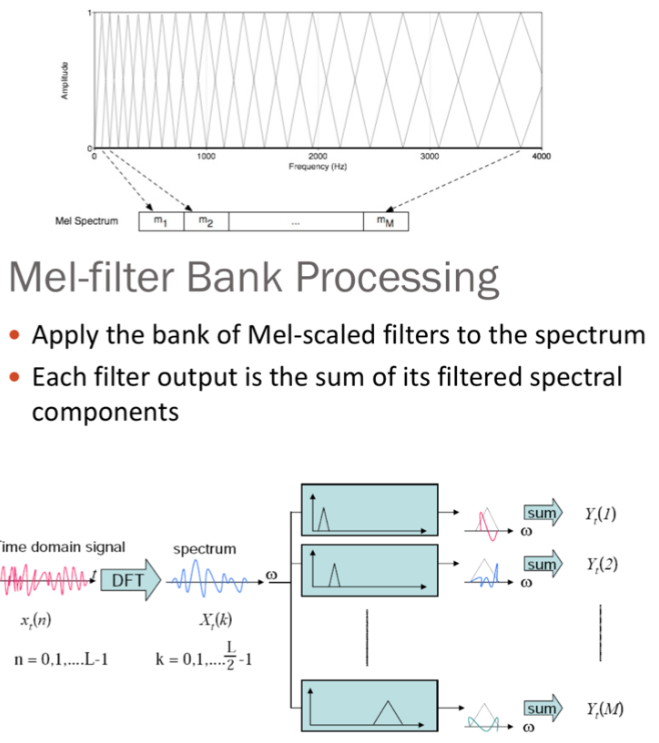
梅尔频率倒谱系数(MFCC)，MFCC首先计算信号的功率谱，然后用滤波器组和离散余弦变换的组合来提取特征。人耳在接收声音时呈现非线性状态，对高频的更不敏感，因此Mel刻度在低频区分辨度较高，在高频区分辨度较低，与频率之间的换算关系。滤波器组中的每个滤波器都是三角形的，中心频率为f(m) ，中心频率处的响应为1，并向0线性减小，直到达到两个相邻滤波器的中心频率，其中响应为0，各f(m)之间的间隔随着m值的增大而增宽。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5ZuRTdyB-1671375120745)(null)]

import numpy
import scipy.io.wavfile
from scipy.fftpack import dct

sample_rate, signal = scipy.io.wavfile.read('OSR_us_000_0010_8k.wav') 
signal = signal[0:int(3.5 * sample_rate)]  # 我们只取前3.5s
# 欲加重处理
emphasized_signal = numpy.append(signal[0], signal[1:] - pre_emphasis * signal[:-1])
# 分帧
frame_length, frame_step = frame_size * sample_rate, frame_stride * sample_rate  # 从秒转换为采样点
signal_length = len(emphasized_signal)
frame_length = int(round(frame_length))
frame_step = int(round(frame_step))
# 确保我们至少有1帧
num_frames = int(numpy.ceil(float(numpy.abs(signal_length - frame_length)) / frame_step))  

pad_signal_length = num_frames * frame_step + frame_length
z = numpy.zeros((pad_signal_length - signal_length))
# 填充信号，确保所有帧的采样数相等，而不从原始信号中截断任何采样
pad_signal = numpy.append(emphasized_signal, z) 

indices = numpy.tile(numpy.arange(0, frame_length), (num_frames, 1)) + numpy.tile(numpy.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
frames = pad_signal[indices.astype(numpy.int32, copy=False)]
# 加窗处理
frames *= numpy.hamming(frame_length)
# FFT 变换
mag_frames = numpy.absolute(numpy.fft.rfft(frames, NFFT))   # fft的幅度(magnitude)
# 计算功率谱
pow_frames = ((1.0 / NFFT) * ((mag_frames) ** 2))  # 功率谱
nfilt = 40
low_freq_mel = 0
high_freq_mel = (2595 * np.log10(1 + (sample_rate / 2) / 700))  # 将Hz转换为Mel
# 我们要做40个滤波器组，为此需要42个点，这意味着在们需要low_freq_mel和high_freq_mel之间线性间隔40个点
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2)  # 使得Mel scale间距相等
hz_points = (700 * (10 ** (mel_points / 2595) - 1))  # 将Mel转换回-Hz
# bin = sample_rate/NFFT    # frequency bin的计算公式
# bins = hz_points/bin=hz_points*NFFT/ sample_rate    # 得出每个hz_point中有多少frequency bin
bins = np.floor((NFFT + 1) * hz_points / sample_rate)

fbank = np.zeros((nfilt, int(np.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
    f_m_minus = int(bins[m - 1])  # 左
    f_m = int(bins[m])  # 中
    f_m_plus = int(bins[m + 1])  # 右

    for k in range(f_m_minus, f_m):
        fbank[m - 1, k] = (k - bins[m - 1]) / (bins[m] - bins[m - 1])
    for k in range(f_m, f_m_plus):
        fbank[m - 1, k] = (bins[m + 1] - k) / (bins[m + 1] - bins[m])
filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)  # 数值稳定性
filter_banks = 20 * np.log10(filter_banks)  # dB
#梅尔频率倒谱系数（MFCCs）
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1 : (num_ceps + 1)] # 保持在2-13
# 均值归一化处理
mfcc -= (numpy.mean(mfcc, axis=0) + 1e-8)

2.3.3. 频谱图

频谱图表示语音信号的功率随频率变化的规律，信号频率与能量的关系用频谱表示，频谱图的横轴为频率，变化为采样率的一半（奈奎斯特采样定理），**纵轴为频率的强度（功率），**以分贝（dB）为单位

语谱图：横坐标是时间**，纵坐标是频率，坐标点值为语音数据能量，**能量值的大小是通过颜色来表示的，颜色越深表示该点的能量越强。一条条横方向的条纹，称为“声纹”。

[Y,FS]=audioread('p225_355_wb.wav');

% specgram(Y,2048,44100,2048,1536);
    %Y1为波形数据
    %FFT帧长2048点(在44100Hz频率时约为46ms)
    %采样频率44.1KHz
    %加窗长度，一般与帧长相等
    %帧重叠长度，此处取为帧长的3/4
specgram(Y,2048,FS,2048,1536);
xlabel('时间(s)')
ylabel('频率(Hz)')
title('“概率”语谱图')

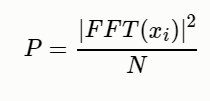
功率谱计算

2.3.4. Librosa 库使用

import matplotlib.pyplot as plt 
import librosa
import librosa.display

y, sr = librosa.load('./train_wb.wav', sr=16000)
# 提取 MFCC feature
mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc=40)
# 提取 mel spectrogram feature
melspec = librosa.feature.melspectrogram(y, sr, n_fft=1024, hop_length=512, n_mels=128)
logmelspec = librosa.power_to_db(melspec)       # 转换为对数刻度
# 绘制 mel 频谱图
plt.figure()
librosa.display.specshow(logmelspec, sr=sr, x_axis='time', y_axis='mel', cmp="jet")
plt.colorbar(format='%+2.0f dB')        # 右边的色度条
plt.title('Beat wavform')
plt.show()

2.3.5. 线性预测系数(LPC)

共振峰出现的频率称为共振峰频率。因此，使用这种技术，通过计算滑动窗口上的线性预测系数，并在随后的线性预测滤波器[17]的频谱中找到峰值，可以预测语音信号中共振峰的位置。LPC有助于在低比特率下对高质量语音进行编码[13,26,27]。从线性预测倒谱系数(LPCC)、对数面积比(LAR)、反射系数(RC)、线谱频率(LSF)和反正弦系数(Arcus Sine coefficients)[13]可以推导出LPC的其他特征。有效地从给定的语音[16]中选择声道信息。

2.3.6. 线性预测倒谱系数(LPCC)

横轴是时间轴，纵轴是振幅轴, 高频语音信号的倒谱分析给出了低频域[29]的小源滤波器可分性。低阶倒谱系数对谱斜率敏感，而高阶倒谱系数对噪声[15]敏感。

2.3.7. 线谱频率(LSF)

LSF图能够在不影响合成语音质量的前提下，将传输线性预测信息的比特率降低25% ~ 30%。除量子化外，预测器的LSF图也适用于插值。从理论上讲，将lsf域平方量化误差与感知相关的对数谱相联系的灵敏度矩阵是对角的[41,42], LSF在语音压缩领域的应用最为突出，并扩展到说话人识别和语音识别领域。LSF还被应用于动物噪音识别、个人工具识别和金融市场分析。LSF的优点包括其对光谱灵敏度的定位能力，它们可以表征带宽和共振位置，并强调了谱峰定位的重要方面。

2.3.8. 小波变换

小波变换是一种信号处理技术，可以高效地表示现实生活中的非平稳信号。它能够在时域和频域同时从瞬态信号中挖掘信息。小波变换将信号分解成一组称为小波的基本函数。小波由一个称为母波的原型小波通过扩展和移位得到。小波变换的主要特点是利用可变窗口扫描频谱，提高了分析的时间分辨率.DWT确实为有效的语音分析[51]提供了足够的频带数。由于输入信号的长度是有限的，由于边界[50]处的不连续性，使得小波系数在边界处的变化非常大。

2.3.9. 感知线性预测(PLP)

	滤波器系数	滤波器的形状	建模方法	速度的计算	系数类型	抗噪声能力	对量化/附加噪声的灵敏度	可靠性	捕获频率
Mel倒频谱系数(MFCC)	Mel	三角形	人类听觉系统	高	倒频谱	中等	中等	高	低
线性预测系数(LPC)	线性预测	线性	人类声道	高	自相关系数	高	高	高	低
线性预测倒谱系数(LPCC)	线性预测	线性	人类声道	中等	倒频谱	高	高	中等	低&中等
谱线频率(LSF)	线性预测	线性	人类声道	中等	频谱	高	高	中等	低&中等
离散小波变换(DWT)	低通&高通	-	-	高	小波	中等	中等	中等	低&中等
感知线性预测(PLP)	Bark	梯形	人类听觉系统	中等	倒频谱&自相关	中等	中等	中等	低&中等

2.4. 采样&下采样

奈奎斯特采样定理，只有采样频率高于声音信号最高频率的两倍时，才能把数字信号表示的声音还原成为原来的声音。带宽：采样频率的一半，最高频率等于采样频率的一半。

2.4.1. 插值法

Volodymyr Kuleshov的论文中使用抗混叠滤波器对语音信号进行下采样，再通过三次样条插值把下采样信号上采样到相同的长度。

from scipy.signal import decimate
import librosa 
import numpy as np 
import matplotlib.pyplot as plt 
from scipy import interpolate

def upsample(x_lr, r):
    """
    上采样，每隔一步去掉语音波形的r个点，然后用三次样条插值的方法把去掉的点补回来，有机会可以画图看看
    :param x_lr:    音频数据
    :param r:       样条插值前个数
    :return:        样条插值后的音频信号
    """
    x_lr = x_lr.flatten()                   # 把x_lr数组折叠成一维的数组
    x_hr_len = len(x_lr) * r
    i_lr = np.arange(x_hr_len, step=r)
    i_hr = np.arange(x_hr_len)

    f = interpolate.splrep(i_lr, x_lr)      # 样条曲线插值系数
    x_sp = interpolate.splev(i_hr, f)       # 给定样条表示的节点和系数，返回在节点处的样条值

    return x_sp


yt, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True)
x_lr = decimate(yt, 2)          # 应用抗混叠滤波器后对信号进行下采样，获得低分辨率音频，下采样因子scale=2

print(len(yt))
print(len(x_lr))

plt.subplot(2, 1, 1)
plt.specgram(yt, Fs=16000, scale_by_freq=True, sides='default')

x_lr = upsample(x_lr, 2)       # 上采样
plt.subplot(2, 1, 2)
plt.specgram(x_lr, Fs=16000, scale_by_freq=True, sides='default')

plt.show()

2.4.2. 重采样（下采样）

import librosa 
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt
y, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) 
#沿给定轴使用傅立叶方法重新采样x到num个样本
f = signal.resample(y, len(y)//2)
f = signal.resample(f, len(y))
plt.subplot(2,1,1)
plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default')
plt.subplot(2,1,2)
plt.specgram(f, Fs=16000, scale_by_freq=True, sides='default')
plt.show()
#         方法二
import librosa 
from scipy import signal
import numpy as np
import matplotlib.pyplot as plt

y, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) 
audio8k = librosa.core.resample(y, wav_fs, wav_fs/2)            # 下采样率 16000-->8000
audio8k = librosa.core.resample(audio8k, wav_fs/2, wav_fs)    # 上采样率 8000-->16000，并不恢复高频部分

plt.subplot(2,1,1)
plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default')

plt.subplot(2,1,2)
plt.specgram(audio8k, Fs=16000, scale_by_freq=True, sides='default')

plt.show()

2.5. 滤波

2.5.1. butterworth低通滤波器

2.5.2. 切比雪夫I形状滤波器

2.5.3. 切比雪夫2形状滤波器

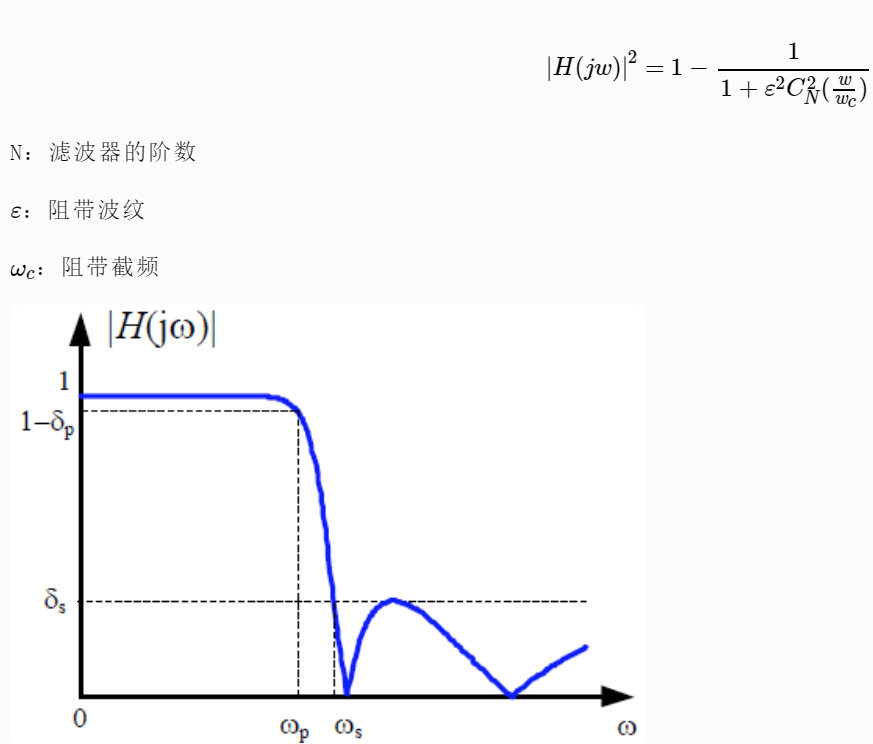
2.5.4. 椭圆低通滤波器

2.5.5. 频域滤波

含噪信号是高能信号与低能噪声叠加的信号，可以通过傅里叶变换的频域滤波实现降噪。https://github.com/LXP-Neve/data/blob/master/machine_learning_date/noised.wav

import numpy as np
import numpy.fft as nf
import scipy.io.wavfile as wf
import matplotlib.pyplot as plt

# 读取音频文件
sample_rate, noised_sigs = wf.read('./da_data/noised.wav')
print(sample_rate)  # sample_rate：采样率44100
print(noised_sigs.shape)    # noised_sigs:存储音频中每个采样点的采样位移(220500,)
times = np.arange(noised_sigs.size) / sample_rate

plt.figure('Filter')
plt.subplot(221)
plt.title('Time Domain', fontsize=16)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[:178], noised_sigs[:178], c='orangered', label='Noised')
plt.legend()

# 傅里叶变换后，绘制频域图像
freqs = nf.fftfreq(times.size, times[1] - times[0])
complex_array = nf.fft(noised_sigs)
pows = np.abs(complex_array)

plt.subplot(222)
plt.title('Frequency Domain', fontsize=16)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
# 指数增长坐标画图
plt.semilogy(freqs[freqs > 0], pows[freqs > 0], c='limegreen', label='Noised')
plt.legend()

# 寻找能量最大的频率值
fund_freq = freqs[pows.argmax()]
# where函数寻找那些需要抹掉的复数的索引
noised_indices = np.where(freqs != fund_freq)
# 复制一个复数数组的副本，避免污染原始数据
filter_complex_array = complex_array.copy()
filter_complex_array[noised_indices] = 0
filter_pows = np.abs(filter_complex_array)

plt.subplot(224)
plt.xlabel('Frequency', fontsize=12)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], filter_pows[freqs >= 0], c='dodgerblue', label='Filter')
plt.legend()

filter_sigs = nf.ifft(filter_complex_array).real
plt.subplot(223)
plt.xlabel('Time', fontsize=12)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[:178], filter_sigs[:178], c='hotpink', label='Filter')
plt.legend()

wf.write('./da_data/filter.wav', sample_rate, filter_sigs)
plt.show()

2.6. 信号增强

2.6.1. 加噪声

控制噪声因子

添加的噪声为均值为0，标准差为1的高斯白噪声，有两种方法对数据进行加噪。

def add_noise1(x, w=0.004):
    # w：噪声因子
    output = x + w * np.random.normal(loc=0, scale=1, size=len(x))
    return output

Augmentation = add_noise1(x=wav_data, w=0.004)

控制信噪比

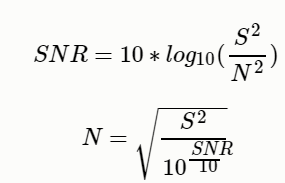
def add_noise2(x, snr):
    # snr：生成的语音信噪比
    P_signal = np.sum(abs(x) ** 2) / len(x)  # 信号功率
    P_noise = P_signal / 10 ** (snr / 10.0)  # 噪声功率
    return x + np.random.randn(len(x)) * np.sqrt(P_noise)

Augmentation = add_noise2(x=wav_data, snr=50)

2.6.2. 波形位移

语音波形移动使用numpy.roll函数向右移动shift距离

numpy.roll(a, shift, axis=None)

def time_shift(x, shift):
    # shift：移动的长度
    return np.roll(x, int(shift))

Augmentation = time_shift(wav_data, shift=fs//2)

2.6.3. 波形拉伸

在不影响音高的情况下改变声音的速度 / 持续时间。这可以使用librosa的time_stretch函数来实现。

def time_stretch(x, rate):
    # rate：拉伸的尺寸，
    # rate > 1 加快速度
    # rate < 1 放慢速度
    return librosa.effects.time_stretch(x, rate)
Augmentation = time_stretch(wav_data, rate=2)

2.6.4. 音高修正

音高修正只改变音高而不影响音速，我发现-5到5之间的步数更合适。

def pitch_shifting(x, sr, n_steps, bins_per_octave=12):
    # sr: 音频采样率
    # n_steps: 要移动多少步
    # bins_per_octave: 每个八度音阶(半音)多少步
    return librosa.effects.pitch_shift(x, sr, n_steps, bins_per_octave=bins_per_octave)

# 向上移三音（如果bins_per_octave为12，则六步）
Augmentation = pitch_shifting(wav_data, sr=fs, n_steps=6, bins_per_octave=12)
# 向上移三音（如果bins_per_octave为24，则3步）
Augmentation = pitch_shifting(wav_data, sr=fs, n_steps=3, bins_per_octave=24)
# 向下移三音（如果bins_per_octave为12，则六步）
Augmentation = pitch_shifting(wav_data, sr=fs, n_steps=-6, bins_per_octave=12)

2.7. 语音度量

2.7.1. 信噪比SNR

有用信号功率与噪声功率的比（此处功率为平均功率），也等于幅度比的平方。

2.7.2. 峰值信噪比（PSNR）

2.7.3. 分段信噪比（SegSNR）

由于语音信号是一种缓慢变化的短时平稳信号，因而在不同时间段上的信噪比也应不一样。为了改善上面的问题，可以采用分段信噪比。分段信噪比即是先对语音进行分帧，然后对每一帧语音求信噪比，最好求均值。

3. 语音识别

import os
import numpy as np
import scipy.io.wavfile as wf
import python_speech_features as sf
import hmmlearn.hmm as hl


# 1. 读取training文件夹中的训练音频样本，每个音频对应一个mfcc矩阵，每个mfcc都有一个类别(apple...)
def search_file(directory):
    """
    :param directory: 训练音频的路径
    :return: 字典{'apple':[url, url, url ... ], 'banana':[...]}
    """
    # 使传过来的directory匹配当前操作系统
    directory = os.path.normpath(directory)
    objects = {}
    # curdir：当前目录
    # subdirs: 当前目录下的所有子目录
    # files: 当前目录下的所有文件名
    for curdir, subdirs, files in os.walk(directory):
        for file in files:
            if file.endswith('.wav'):
                label = curdir.split(os.path.sep)[-1]  # os.path.sep为路径分隔符
                if label not in objects:
                    objects[label] = []
                # 把路径添加到label对应的列表中
                path = os.path.join(curdir, file)
                objects[label].append(path)
    return objects


# 读取训练集数据
train_samples = search_file('../machine_learning_date/speeches/training')

"""
2. 把所有类别为apple的mfcc合并在一起，形成训练集。
    训练集:
    train_x：[mfcc1,mfcc2,mfcc3,...],[mfcc1,mfcc2,mfcc3,...]...
    train_y：[apple],[banana]...
由上述训练集样本可以训练一个用于匹配apple的HMM。"""

train_x, train_y = [], []
# 遍历字典
for label, filenames in train_samples.items():
    # [('apple', ['url1,,url2...'])
    # [("banana"),("url1,url2,url3...")]...
    mfccs = np.array([])
    for filename in filenames:
        sample_rate, sigs = wf.read(filename)
        mfcc = sf.mfcc(sigs, sample_rate)
        if len(mfccs) == 0:
            mfccs = mfcc
        else:
            mfccs = np.append(mfccs, mfcc, axis=0)
    train_x.append(mfccs)
    train_y.append(label)

# 3.训练模型，有7个句子，创建了7个模型
models = {}
for mfccs, label in zip(train_x, train_y):
    model = hl.GaussianHMM(n_components=4, covariance_type='diag', n_iter=1000)
    models[label] = model.fit(mfccs)  # # {'apple':object, 'banana':object ...}

"""
4. 读取testing文件夹中的测试样本，
    测试集数据：
        test_x  [mfcc1, mfcc2, mfcc3...]
        test_y  [apple, banana, lime]
"""
test_samples = search_file('../machine_learning_date/speeches/testing')

test_x, test_y = [], []
for label, filenames in test_samples.items():
    mfccs = np.array([])
    for filename in filenames:
        sample_rate, sigs = wf.read(filename)
        mfcc = sf.mfcc(sigs, sample_rate)
        if len(mfccs) == 0:
            mfccs = mfcc
        else:
            mfccs = np.append(mfccs, mfcc, axis=0)
    test_x.append(mfccs)
    test_y.append(label)


# 5.测试模型
#    1. 分别使用7个HMM模型，对测试样本计算score得分。
#    2. 取7个模型中得分最高的模型所属类别作为预测类别。
pred_test_y = []
for mfccs in test_x:
    # 判断mfccs与哪一个HMM模型更加匹配
    best_score, best_label = None, None
    # 遍历7个模型
    for label, model in models.items():
        score = model.score(mfccs)
        if (best_score is None) or (best_score < score):
            best_score = score
            best_label = label
    pred_test_y.append(best_label)

print(test_y)   # ['apple', 'banana', 'kiwi', 'lime', 'orange', 'peach', 'pineapple']
print(pred_test_y)  # ['apple', 'banana', 'kiwi', 'lime', 'orange', 'peach', 'pineapple']

4. 主动降噪（ANC）

通过降噪系统产生与外界噪音相等的反向声波，将噪声中和，从而实现降噪的效果。所有的声音都由一定的频谱组成，如果可找到一种声音，其频率、振幅与所要消除的噪声完全一样，只是相位刚好相反(相差 $180^o$ )就可以将这噪声完全抵消。ANC降噪对2KHZ以下的信号噪声降噪效果比较好，对高频噪声降噪效果很差。原因为高频信号波长短，对相位偏差也比较敏感，导致ANC对高频噪声降噪效果差。一般高频噪声可以被耳机物理的遮蔽屏蔽掉，这种降噪被称为被动降噪。

被动降噪：被动式降噪也就是物理降噪，被动式降噪是指利用物理特性将外部噪声与耳朵隔绝开，主要通过耳机的头梁设计得紧一些、耳罩腔体进行声学优化、耳罩内部放上吸声材料……等等来实现耳机的物理隔音。被动降噪对高频率声音（如人声）的隔绝非常有效，一般可使噪声降低大约为15-20dB。

4.1. ENC降噪

ENC（Environmental Noise Cancellation，环境降噪技术），能有效抑制90%的反向环境噪声，由此降低环境噪声最高可达35dB以上，让游戏玩家可以更加自由的语音沟通。通过双麦克风阵列，精准计算通话者说话的方位，在保护主方向目标语音的同时，去除环境中的各种干扰噪声。

4.2. DSP降噪

DSP是英文(digital signal processing)的简写。主要是针对高、低频噪声。工作原理是麦克风收集外部环境噪音，然后系统复制一个与外界环境噪音相等的反向声波，将噪音抵消，从而达到更好的降噪效果。DSP降噪的原理和ANC降噪相似。但DSP降噪正反向噪音直接在系统内部相互中和抵消。

4.3. CVC降噪

CVC（Clear Voice Capture）是通话软件降噪技术。主要针对通话过程中产生的回声。通过全双工麦克风消噪软件，提供通话的回声和环境噪音消除功能，是目前蓝牙通话耳机中最先进的降噪技术。

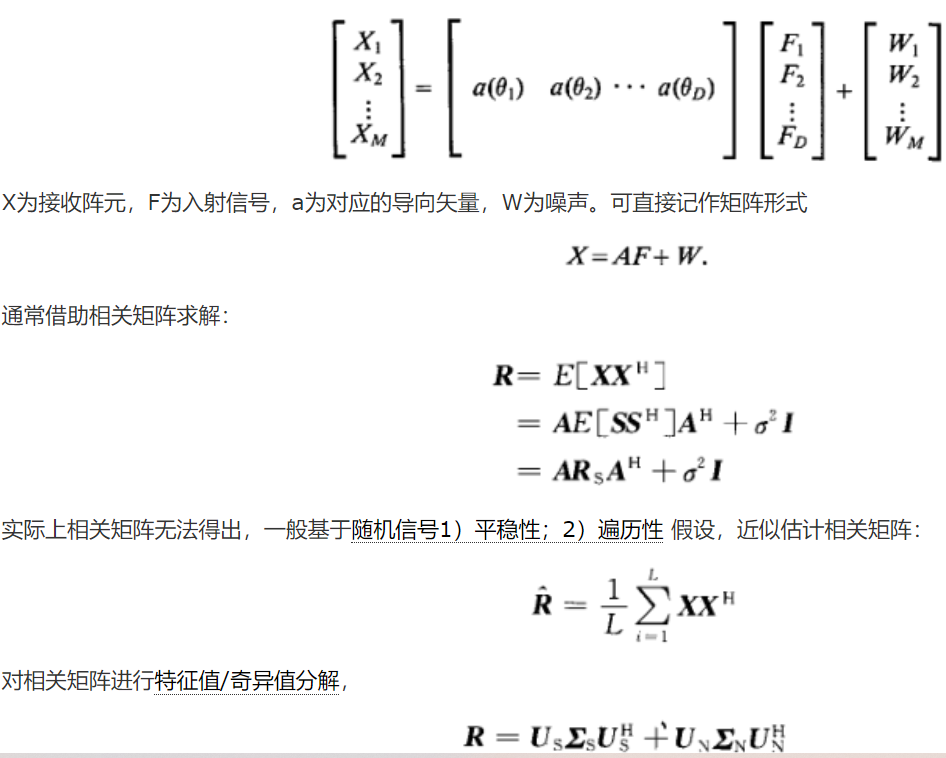
5. 声源定位

FRIDA和MUSIC算法的鲁棒性较好，其次是SRP-PHAT和TOPS，再次WAVES和CSSM算法。

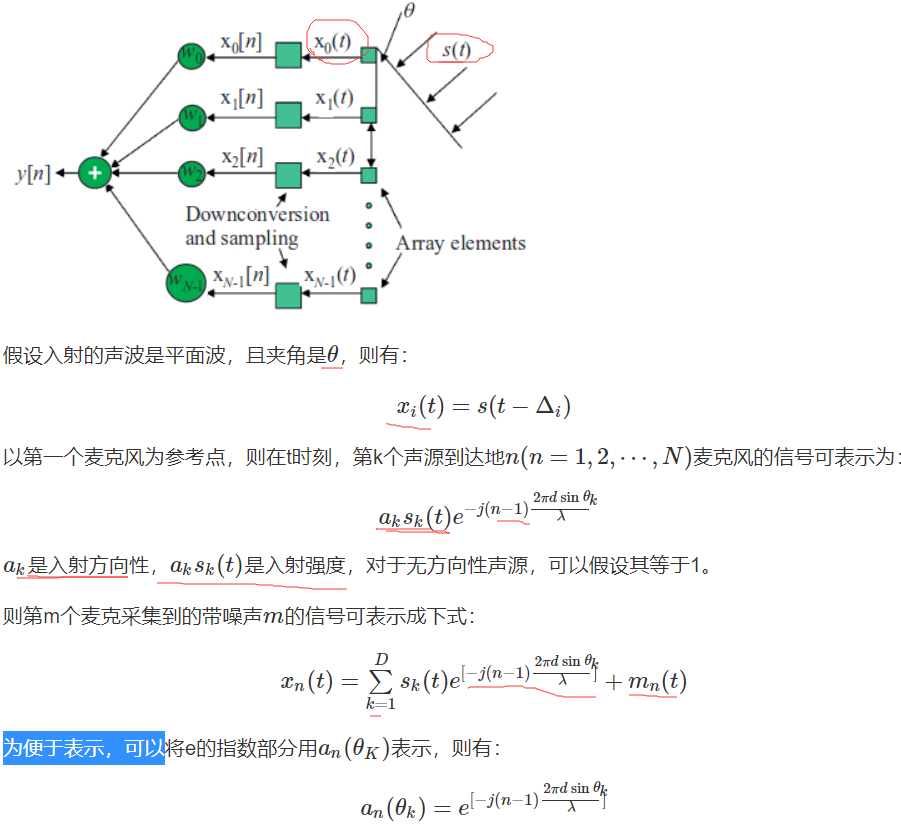
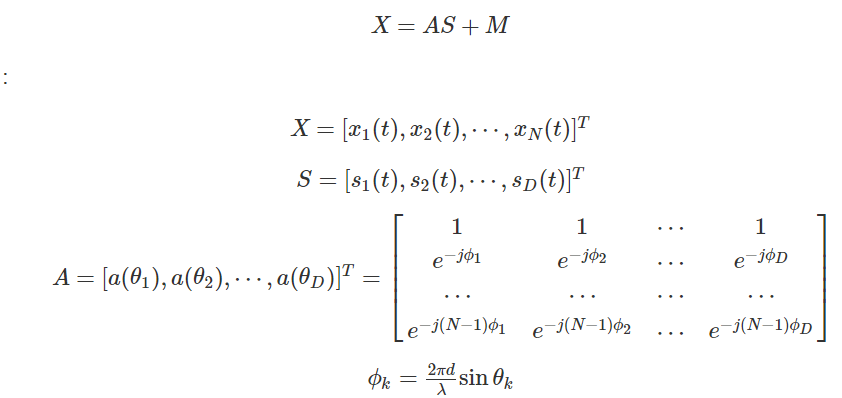
5.1. GCC-SRP

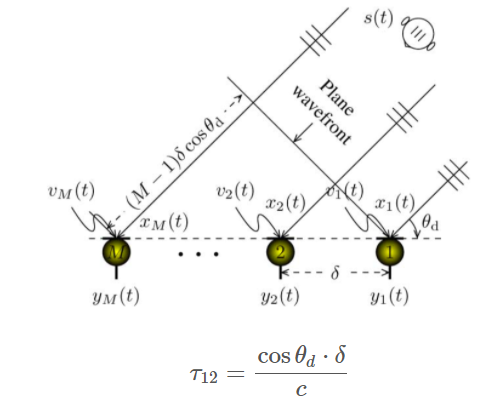
互相关方法具有计算量小，实时性好而被大多数系统中使用，其基于阵元之间的差异时间差(Time-Delay/Frequency-Delay)进而提取出声源距离阵元的位置信息，根据不同的麦克风对就可以在三维空间中唯一确定一个声源. 基本思想是在可能的空间点中做波束合成，然后根据合成后的各个方向上的功率最大值认为是声源方法。用GCC-PHAT方法得到具有陡峭峰值互相关函数，找到互相关最大时的点，结合采样频率Fs与与麦克风间距dFs与与麦克风间距d，就可以得到方向信息。

互相关可以用来描述两个信号之间的相似性;离散信号xk,yk的互相关函数定义为:
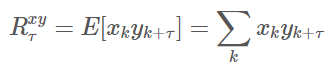
取使得互相关系数最大的延时值作为TDOA的估计:

5.2. Music

5.3. TOPS

通过信号和噪声子空间多个频率成分的正交关系估计声源方位，TOPS可用于一维和二维阵列.

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5wJErv7t-1671375120887)(null)]

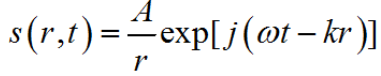
窄带编辑

窄带意味着信号在阵列上的延迟比信号的时域宽度小得多，从而信号包络沿这列的延迟可以忽略不计，故阵列孔径内的各振元复包络不变。反之，若复包络有变化，则通常认为是宽带信号。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YVpEkQJw-1671375117881)(https://gitee.com/github-25970295/blogImage/raw/master/img/image-20201122143441337.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1bO8oOEF-1671375120590)(null)]

5.4. FRIDA

6. 声源分离

6.1. ML based

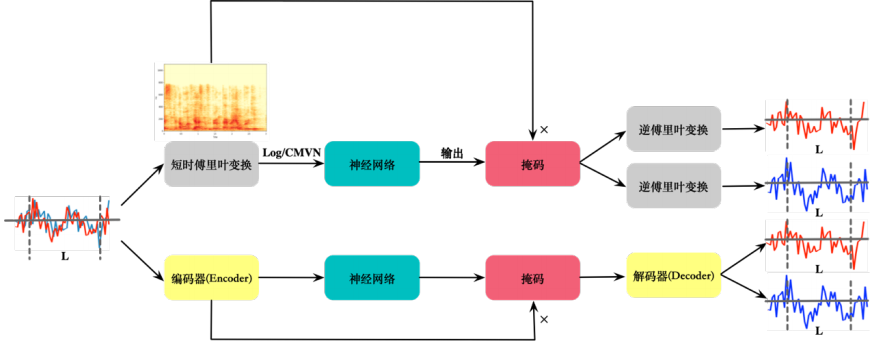
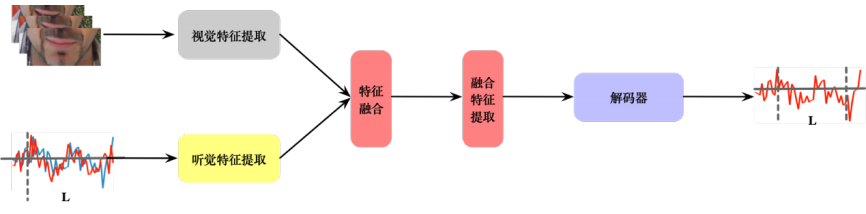
波束形成技术(BF, beamforming) 2.盲源分离技术(BSS, blind source seperation) 3.时频掩码技术(T-F masking, time-frequency masking)

一般使用理想二值掩蔽方法来生产mask，对于时频表示的语音信号，输出有几个信号就会生成几个mask矩阵，以两个说话人为例，在每个时频点比较两个说话人语音能量的大小，将能量大的一方的mask矩阵对应位置的值设为1，另一个mask矩阵的对应位置设为0。

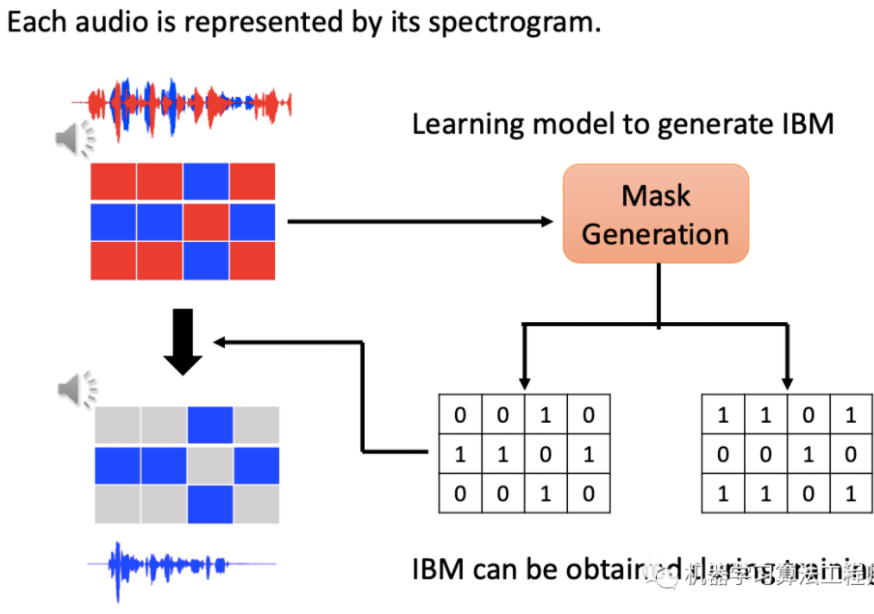
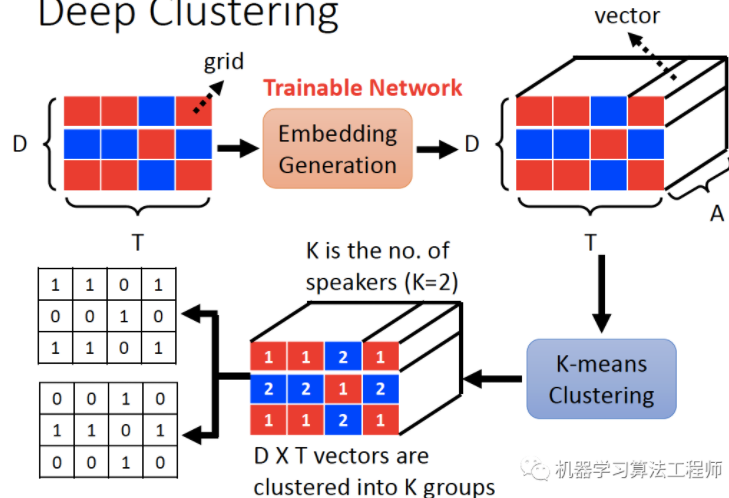
6.2. Deep Clustering

Deep Clustering算法训练神经网络为输入特征中的每个元素生成一个具有区分性的嵌入向量（embedding），之后利用聚类算法，如K-means，对生产的embedding进行聚类，得出不同类别即是不同说话人的信号分离结果图。Deep Clustering性能和泛化性能(训练在英文，测试在中文等情况)都比较好，但缺点是它不是一个end to end的方法，因为聚类方法不能训练。

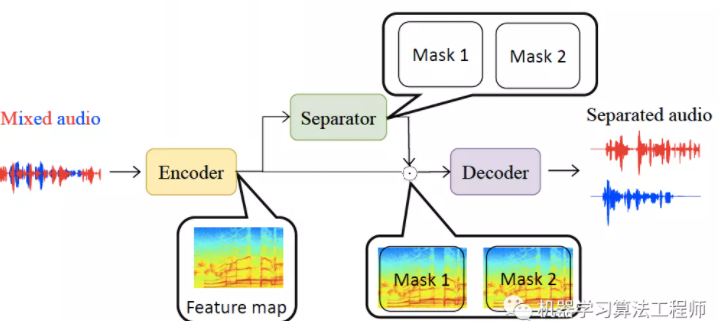
TasNet（Time-domain Audio Separation Network）是时域的方法(直接输入混合语音，不经过STFT等变化得到声音特征)，由编码器、分离网络、解码组成，与频域方法相比，编码过程不是固定的而是网络学到的(论文中认为对于语音而言STFT并不一定是最佳编码方式，有两点证实了此观点，论文中对编码器输出增加非负的约束会使模型变差，对编解码器增加互逆的关联约束使模型变差，即同一信号经过编码器再经过解码器得到同一信号)，通过分离网络得到两个mask，学到的mask与编码器输出相乘再经过解码器得分离的声音，训练过程使用前文提到的PIT方法，编解码器都是一维卷积（相当于全连接层线性变换），实验结果展示幅度和相位信息都被编码器学习到了特征之中。