问题描述

 给定很多线段，每个线段都有两个数[start, end]，

表示线段开始位置和结束位置，左右都是闭区间

规定：

1）线段的开始和结束位置一定都是整数值

2）线段重合区域的长度必须>=1

返回线段最多重合区域中，包含了几条线段

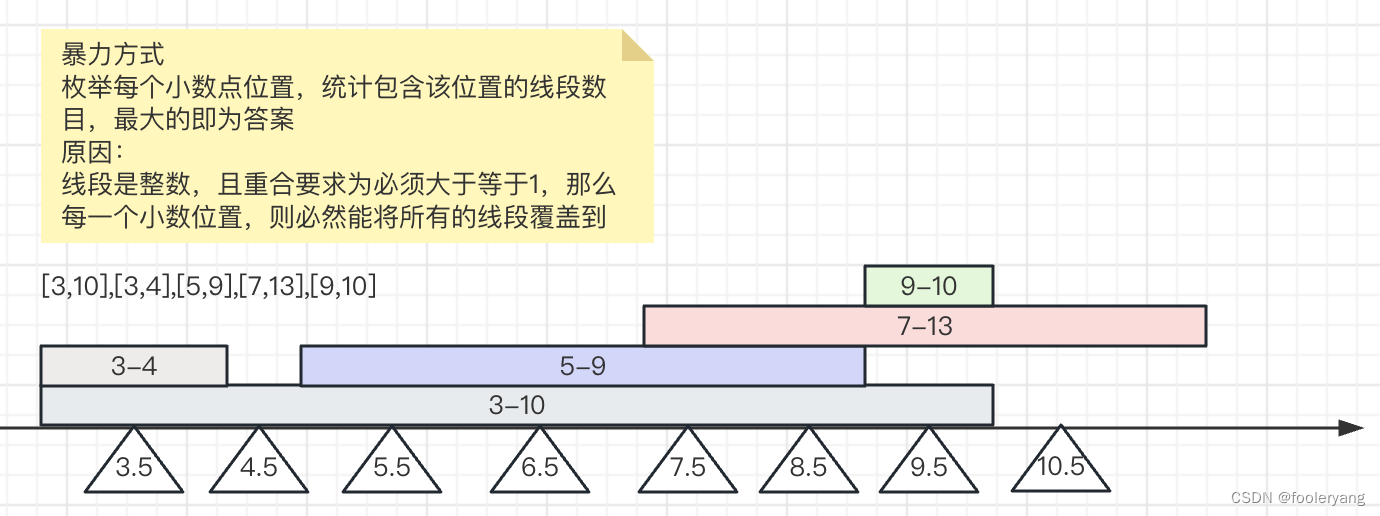
例如：[3,10],[3,4],[5,9],[7,13],[9,10]返回3 

暴力方式解题

思路

先得到线段最小点和最大点，这是所有线段在x轴上的范围 在该范围上，取小数点如0.5进行查看，即查看每个0.5位置，有没有线段包含该点，记录多少条线段 max 用一个变量cover保存所有点中最多覆盖的线段条数 最后得到的cover就是重合区域最多的线段数目

图例

利用小根堆解题

思路

1.将开始点排序后，遍历该数组

2.将堆中所有 <= 当前线段的开始点的数弹出

3.将该点的结束点加入到堆中

4.记录过程中堆的历史最大长度

5.遍历结束后该长度就是其重合最多线段的个数

图例

待排序数组，且以按开始点排序

[3,10],[3,4],[5,9],[7,13],[9,10]

1. 遍历到[3,10]时

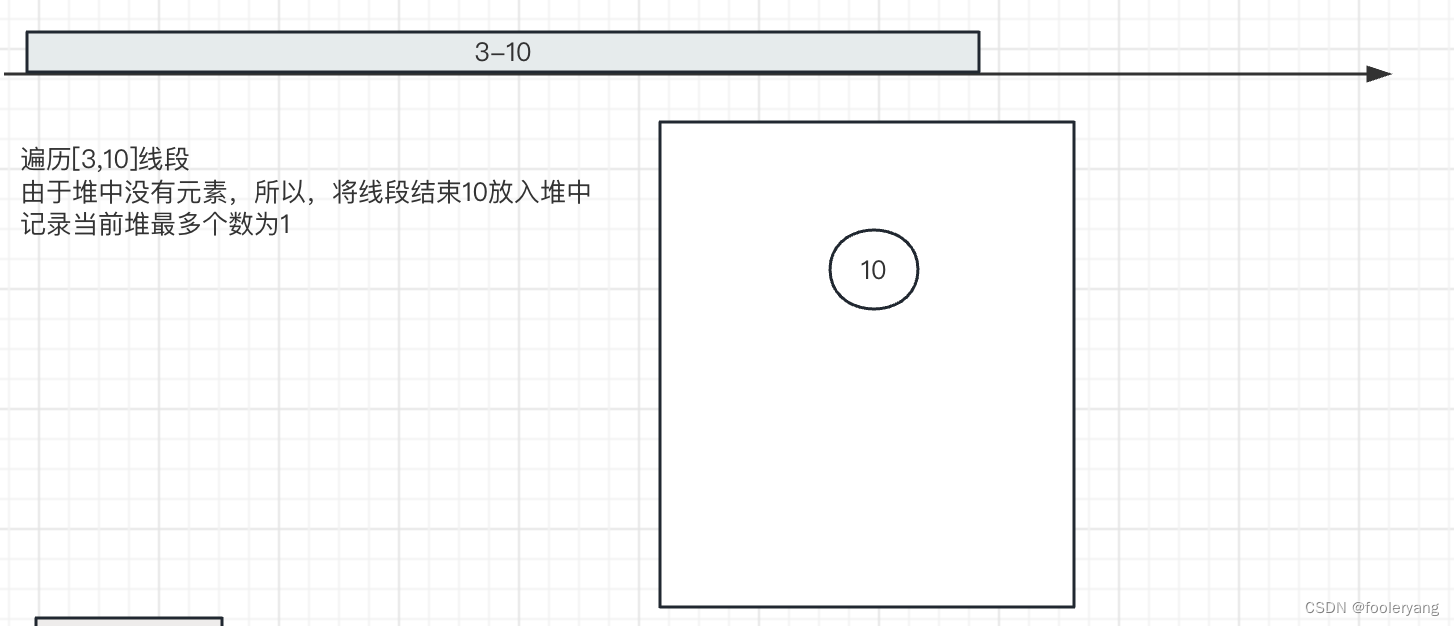
2. 遍历到[3,4]时

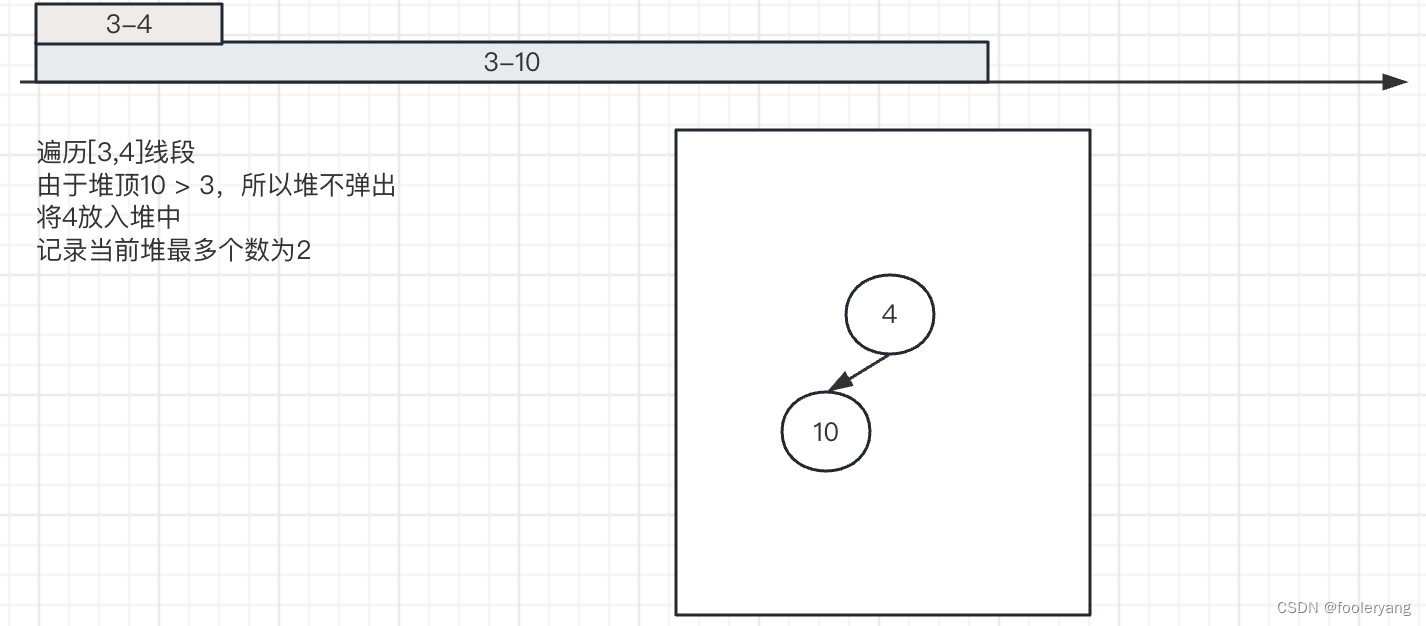
3. 遍历到[5,9]时

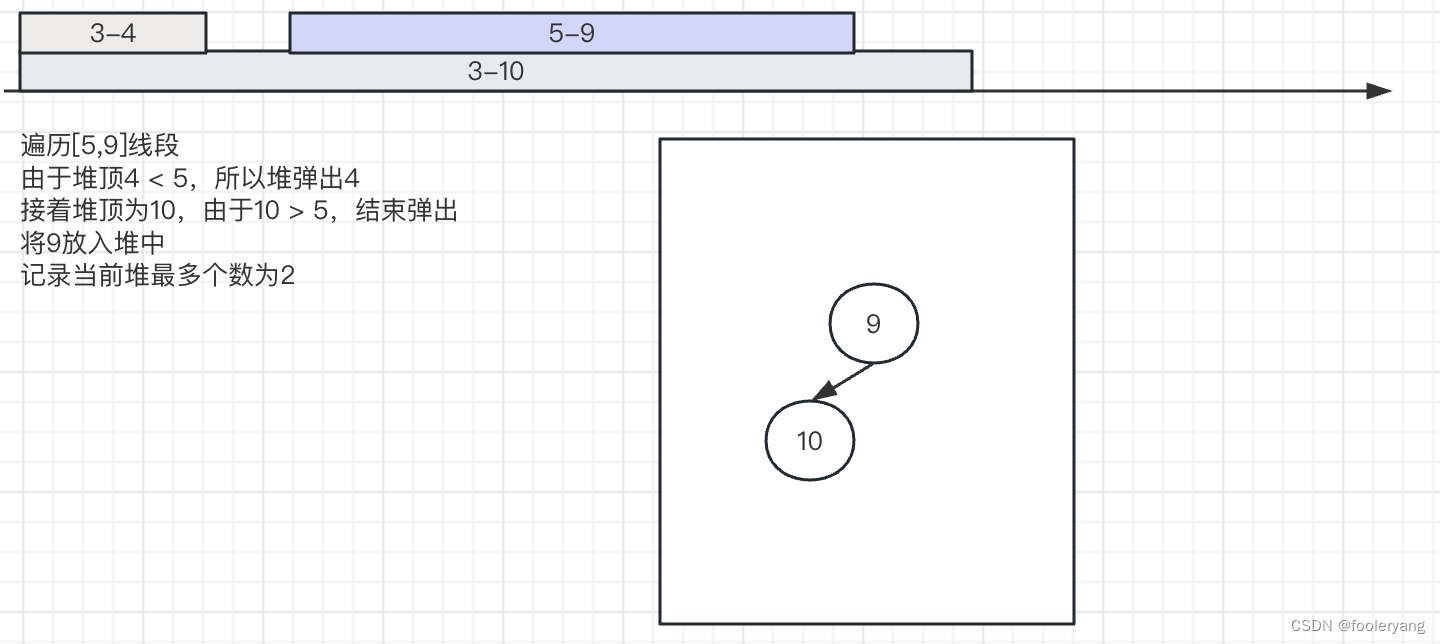
4.遍历到[7,13]时

5.遍历到[9,10]时

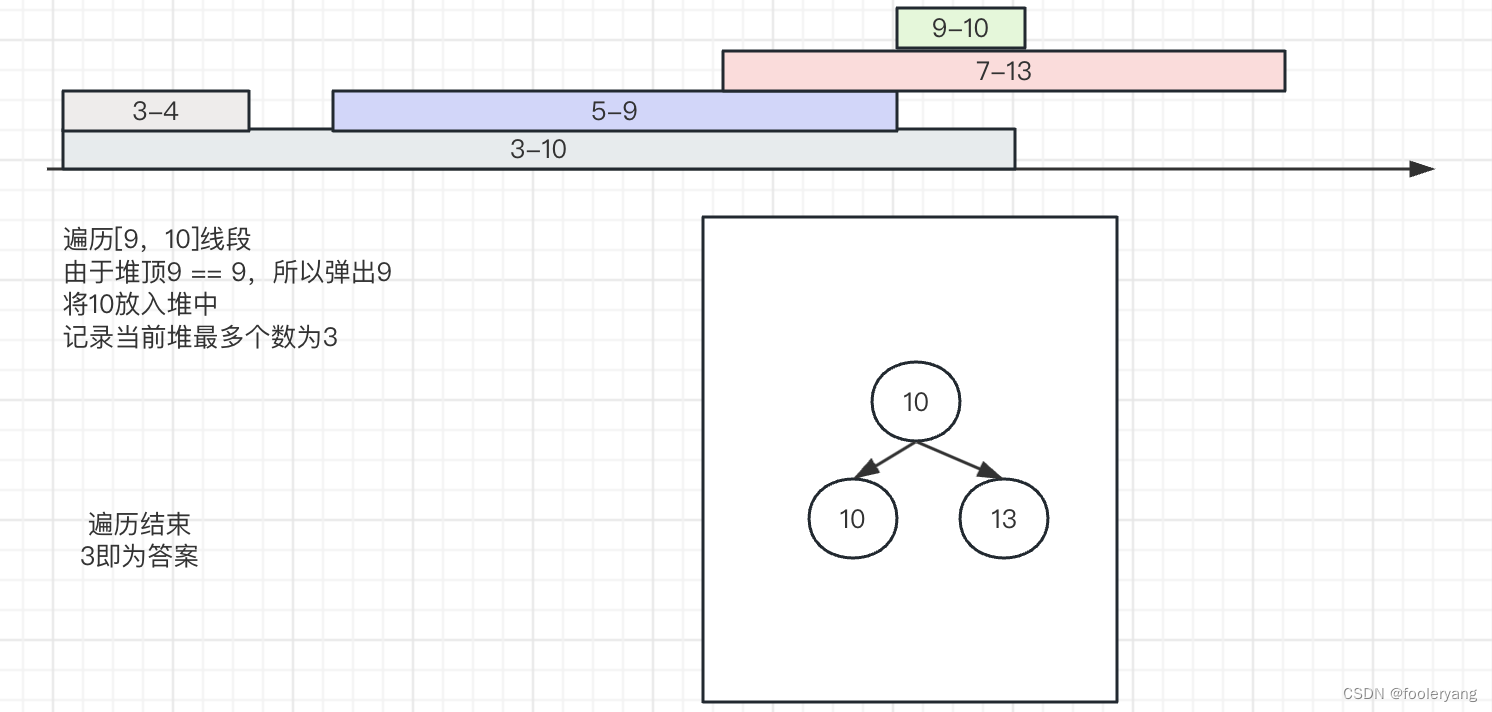
code

public static int coverMax(int [][] lines){
        if(lines.length < 2)
            return 0;
        Arrays.sort(lines, (a, b) -> (a[0] - b[0]));
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        int max = 0;
        for (int [] line : lines){
            while (!minHeap.isEmpty() && minHeap.peek() <= line[0]){
                minHeap.poll();
            }
            minHeap.add(line[1]);
            max = Math.max(max,minHeap.size());
        }
        return max;
}