1 随机数的问题

用 C# Random 类生成的随机数是平均分布的。也就是各数据段的出现的次数差不多。彩票号码属于这种随机数。

而很多很多常见的随机数，比如：成绩，却是符合正态分布的。

因而很多时候需要生成符合正态分布规律的随机数。

2 文本格式的程序

// 定义一个全局性（公共）的随机数发生器，便于大家（各函数）后面共同使用。
Random global_rnd = new Random();

/// <summary>
/// Box-Muller算法
/// 随机产生一个符合正态分布的数 u均数，d为标准方差
/// 注：本算法来自于网络，原文 d 为方差，错误！
/// </summary>
/// <param name="u"></param>
/// <param name="d"></param>
/// <returns></returns>
public double Rand(double u, double d)
{
double u1, u2, z, x;
if (d <= 0)
{
return u;
}
u1 = global_rnd.NextDouble();
u2 = global_rnd.NextDouble();
z = Math.Sqrt(-2 * Math.Log(u1)) * Math.Sin(2 * Math.PI * u2);
x = u + d * z;
return x;
}

/// <summary>
/// 《小白学程序》第十六课：随机数（Random）第三，正态分布的随机数的计算方法与代码
/// 一般的随机数是平均分布的，不符合常见的随机数分布，比如：成绩。
/// 因而很多时候需要生成符合正态分布规律的随机数
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
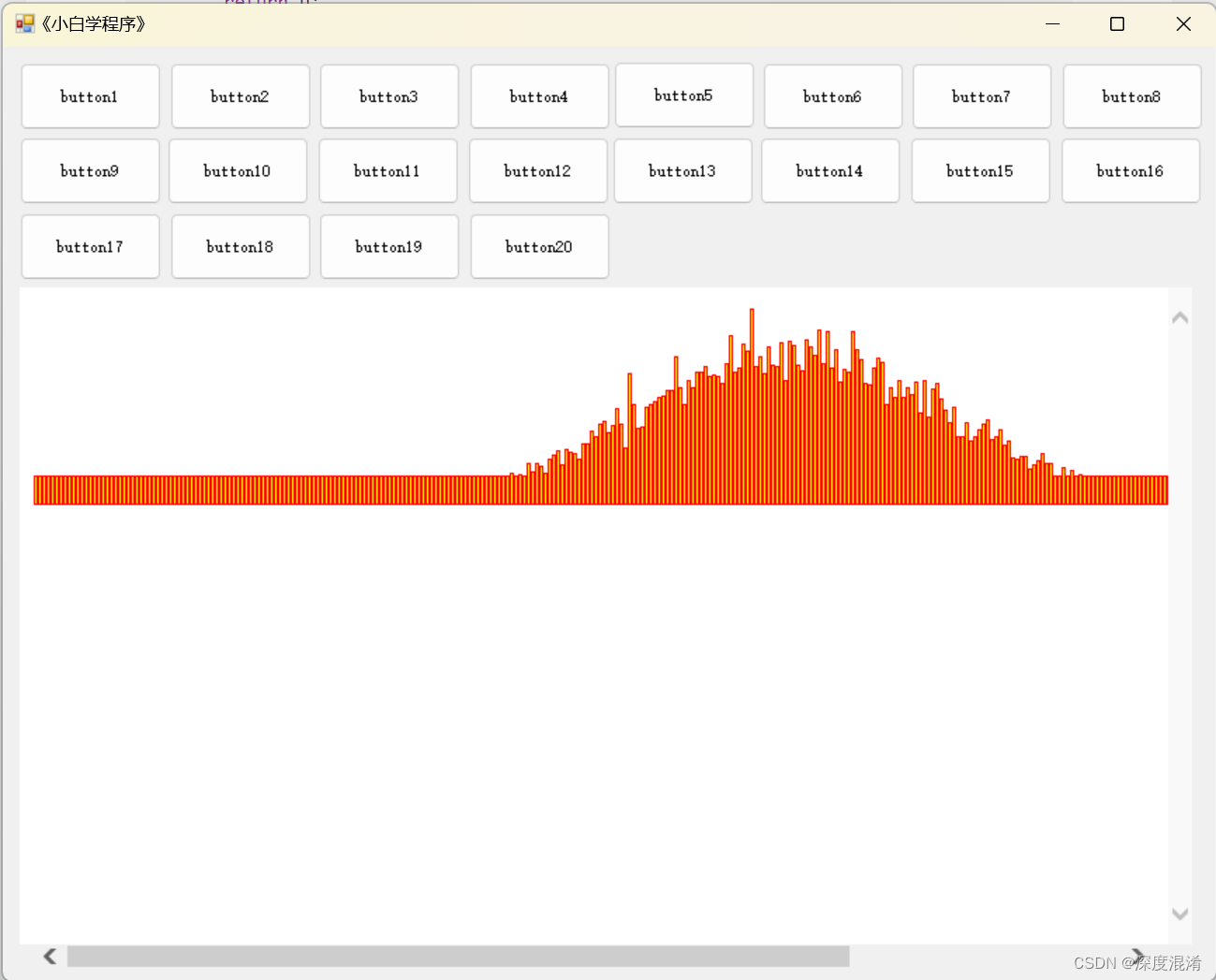
private void button16_Click(object sender, EventArgs e)
{
// 生成随机数，并统计，代码与前一课差不多
int n = 360;
int[] freq = new int[n];
for (int i = 0; i < 10000; i++)
{
// 调用 Rand() 生成符合正态分布的随机数
int a = (int)(Rand(0.5, 0.1) * n);
if (a < 0) continue;
if (a >= n) continue;
freq[a] += 1;
}

// 显示统计结果与前面一节课的类似
// 方柱的高度就是数字出现的次数（频率）
StringBuilder sb = new StringBuilder();
sb.AppendLine("<style>td { padding:0px;text-align:center;text-size:0px; } </style>");
sb.AppendLine("<table width=420 border=0 style='border-collapse:collapse;'>");
sb.AppendLine("<tr>");
for (int i = 0; i < n; i++)
{
sb.Append("<td style='vertical-align:bottom;'>");
sb.Append("<div style='width:3px;height:" + freq[i] + "px;border:solid 1px #FF0000;background-color:rgb(255,255,0);'></div>");
sb.AppendLine("</td>");
}
sb.AppendLine("</tr>");
sb.AppendLine("</table>");

webBrowser1.DocumentText = sb.ToString();
}

3 代码格式


// 定义一个全局性（公共）的随机数发生器，便于大家（各函数）后面共同使用。
Random global_rnd = new Random();

/// <summary>
/// Box-Muller算法
/// 随机产生一个符合正态分布的数 u均数，d为标准方差
/// 注：本算法来自于网络，原文 d 为方差，错误！
/// </summary>
/// <param name="u"></param>
/// <param name="d"></param>
/// <returns></returns>
public double Rand(double u, double d)
{
    double u1, u2, z, x;
    if (d <= 0)
    {
        return u;
    }
    u1 = global_rnd.NextDouble();
    u2 = global_rnd.NextDouble();
    z = Math.Sqrt(-2 * Math.Log(u1)) * Math.Sin(2 * Math.PI * u2);
    x = u + d * z;
    return x;
}

/// <summary>
/// 《小白学程序》第十六课：随机数（Random）第三，正态分布的随机数的计算方法与代码
/// 一般的随机数是平均分布的，不符合常见的随机数分布，比如：成绩。
/// 因而很多时候需要生成符合正态分布规律的随机数
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
private void button16_Click(object sender, EventArgs e)
{
    // 生成随机数，并统计，代码与前一课差不多
    int n = 360;
    int[] freq = new int[n];
    for (int i = 0; i < 10000; i++)
    {
        // 调用 Rand() 生成符合正态分布的随机数
        int a = (int)(Rand(0.5, 0.1) * n);
        if (a < 0) continue;
        if (a >= n) continue;
        freq[a] += 1;
    }

    // 显示统计结果 与 前面一节课 的类似
    // 方柱 的高度就是数字出现的次数（频率）
    StringBuilder sb = new StringBuilder();
    sb.AppendLine("<style>td { padding:0px;text-align:center;text-size:0px; } </style>");
    sb.AppendLine("<table width=420 border=0 style='border-collapse:collapse;'>");
    sb.AppendLine("<tr>");
    for (int i = 0; i < n; i++)
    {
        sb.Append("<td style='vertical-align:bottom;'>");
        sb.Append("<div style='width:3px;height:" + freq[i] + "px;border:solid 1px #FF0000;background-color:rgb(255,255,0);'></div>");
        sb.AppendLine("</td>");
    }
    sb.AppendLine("</tr>");
    sb.AppendLine("</table>");

    webBrowser1.DocumentText = sb.ToString();
}