文章目录
- 1. 损失函数、期望风险、经验风险
- 2. 经验风险最小化和结构风险最小化
- 2.1 结构风险(正则化)
- 2.2 两者的定义
- 3. 训练误差 与 测试误差
- 4. 过拟合 与 欠拟合
- 4.1 过拟合及解决方法
- 4.2 交叉验证
- 4.3 欠拟合
- 5. 泛化误差 与 泛化误差上界
- 5.1 泛化误差
- 5.2 泛化误差上界
- 6. 生成模型 与 判别模型
- 7. 最大似然估计
- 7.1 极大似然估计
- 7.2 最大似然估计 与 经验风险 关系
1. 损失函数、期望风险、经验风险
-
常见的损失函数:

注意:损失函数不一定是上面的4个,也可以自定义损失函数。比如:感知机的损失函数就是自定义:误分类点到超平面的距离。
-
期望风险

-
经验风险

2. 经验风险最小化和结构风险最小化
2.1 结构风险(正则化)
结构风险:指为经验风险加上正则项,用于对模型的参数个数(即模型复杂度)进行限制
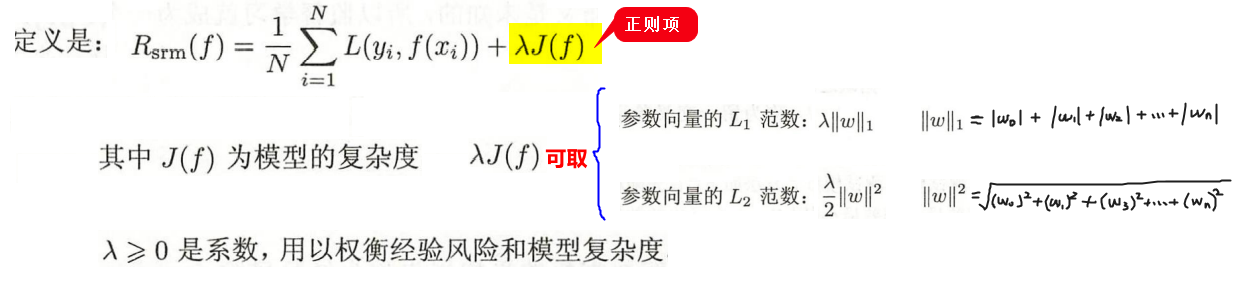
2.2 两者的定义
用于表明什么是最优模型,即求最小化的目标函数是谁?
-
经验风险最小化:指经验风险最小的模型就是最优模型。
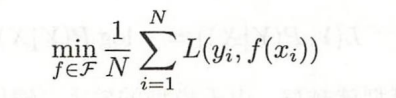
-
结构风险最小化:为了防止过拟合而提出来的,指结构风险最小的模型就是最优模型。

因此,在机器学习三要素中,第三步使用算法求解最优模型时,有两个角度。
3. 训练误差 与 测试误差
-
训练误差:模型在训练集上的经验风险
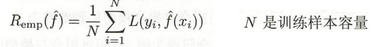
-
测试误差:模型在测试集上的经验风险
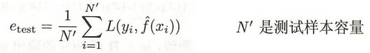
4. 过拟合 与 欠拟合
4.1 过拟合及解决方法
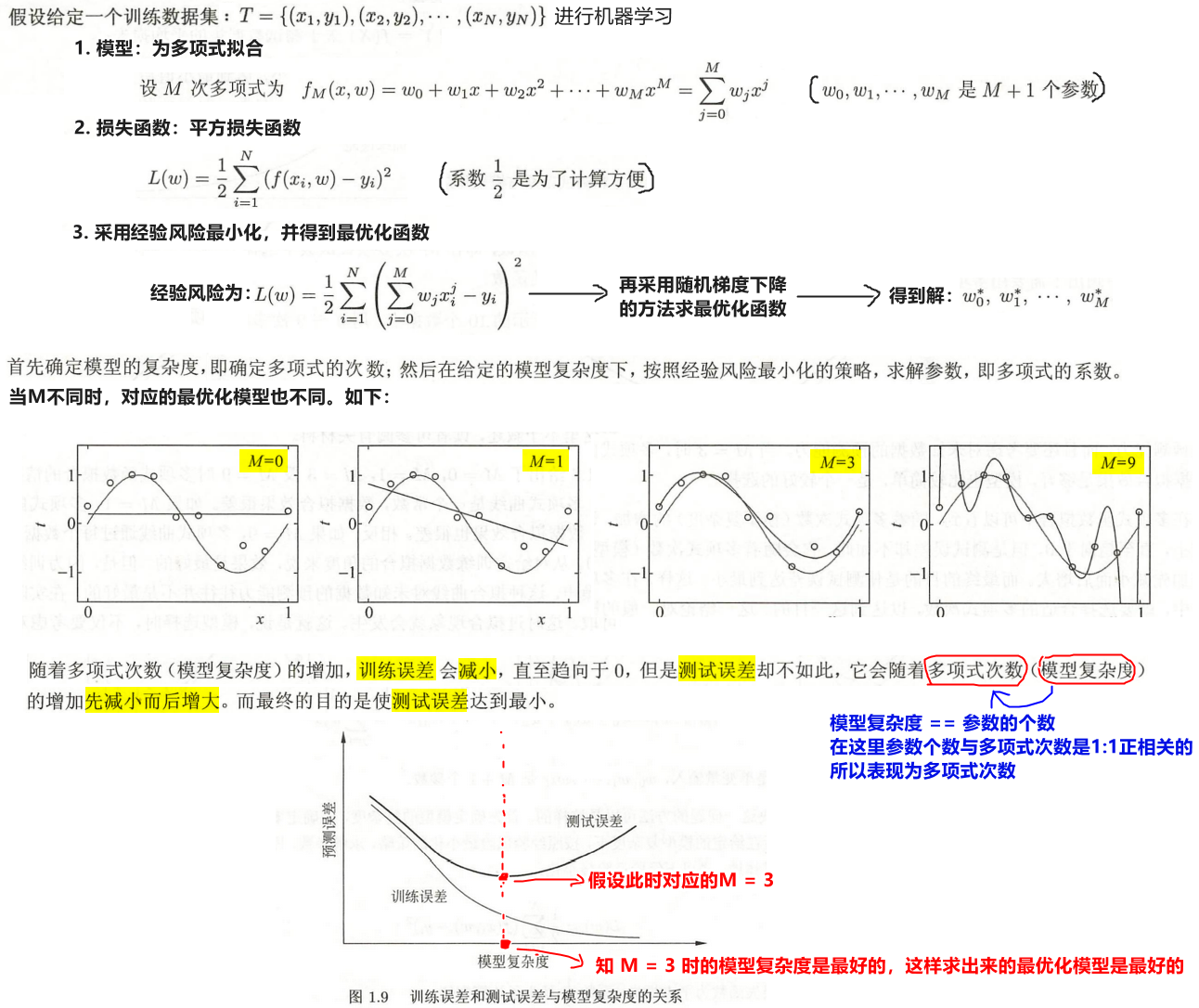
- 过拟合:求得的最优模型过于复杂导致预测效果不好。 比如上面的
M = 4时求得的最优化模型,虽然训练误差为,但是训练误差缺很大。而评价一个模型的好坏是根据泛化能力(≈ 泛化误差上界 ≈ 测试误差) 来衡量的,训练误差越小越好。 - 解决方法:
① 增加样本量 【为什么增加样本量可以防止过拟合?具体见泛化误差上界这一节】
② 交叉验证:取参数复杂度的平均,故可以防止过拟合。
③ 使用结构风险最小化而不是经验风险最小化【为什么结构风险最小化可以防止过拟合?见“正则化”这一节】
4.2 交叉验证
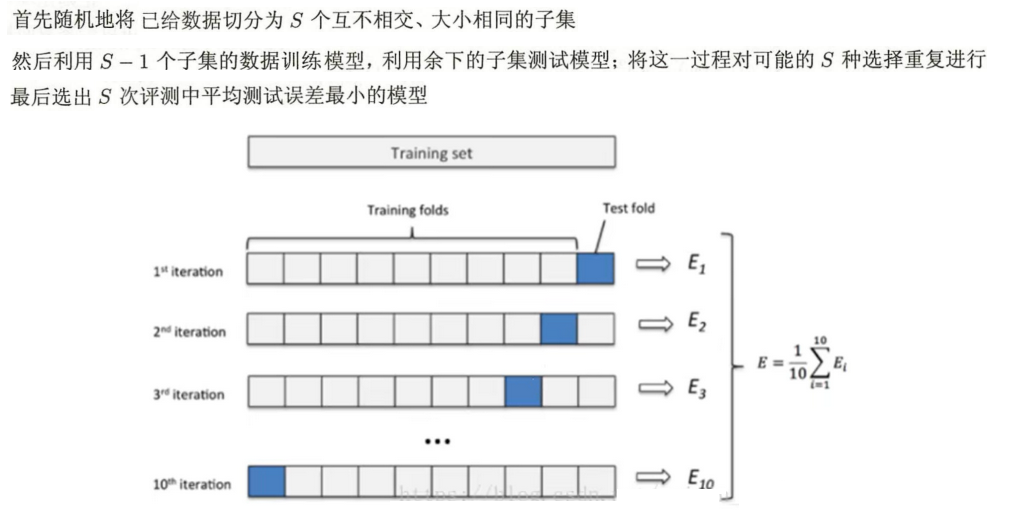
4.3 欠拟合
5. 泛化误差 与 泛化误差上界
5.1 泛化误差
-
泛化误差:指模型在测试集上的期望风险。
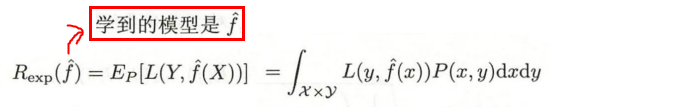
区分:测试误差是模型在测试集上的经验风险。
-
作用:对于不同复杂度下得到的最优化模型,我们可以使用泛化误差来衡量模型的好坏。泛化误差越小,模型越好。
5.2 泛化误差上界
和期望风险与经验风险的一样,由于 P(x, y) 是不知道的,也求不出来,所以转而使用 泛化误差上界 来代替 泛化误差去评估模型的好坏。

- 可以观察到 泛化误差上界 与 N成反比,所以样本容量越大,模型越好。这就解释了为什么增加样本容量可以防止过拟合。
- 可以观察到 泛化误差上界 与 d成反比。参数越多,d越大,导致泛化误差上界越大,模型就越差。
注意:有时候近似的用 测试误差 来代替 泛化误差上界。
6. 生成模型 与 判别模型
注意:生成模型 与 判别模型 都是监督学习中的概念。而监督模型中的模型模型有两类:
概率模型P(y | x)与决策模型 y = f(x)。
-
定义:

-
区别 / 特点:
- ① 生成模型关心的是输入x与输出y的关系。即关心训练数据本身的特性,而不关心各类的边界在哪;
② 判别模型关心的是输入x,该输出什么y,关心各类的边界在哪,而不关心训练数据本身的特性。 - 根据公式容易知道:由生成模型可以得到判别模型,但由判别模型得不到生成模型。
- 当存在隐变量(当我们找不到引起某一现象的原因的时候,我们就把这个在起作用但是无法确定的因素,叫“隐变量”) 时,仍可以利用生成方法学习,此时判别方法不能用。
- 生成模型收敛速度快
- 判别模型的准确率高
- 判别模型是直接求决策模型或概率模型,所以抽象程度更高,往往可以用来简化问题。
- ① 生成模型关心的是输入x与输出y的关系。即关心训练数据本身的特性,而不关心各类的边界在哪;
-
代表算法:

-
例子1:

-
例子2:
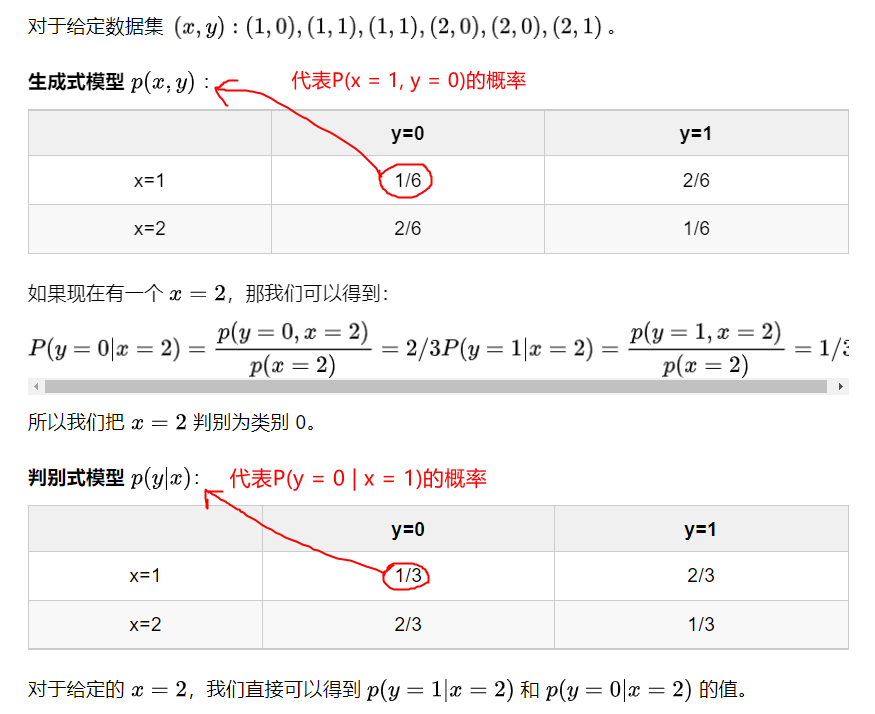
7. 最大似然估计
7.1 极大似然估计
- 区分:概率 与 似然
- 概率 是已知模型和参数,去预测数据。
- 似然 是已知数据,推模型和参数。
- 概率函数与似然函数:对于P(x | θ) 函数,x表示某一个具体的数据;θ 表示模型的参数。
- 如果参数θ已知,样本x未知,是推数据,所以P(x | θ) 函数叫概率函数。
- 如果参数x已知,样本θ未知,是推参数,所以P(x | θ) 函数叫似然函数。
似然函数的自变量是θ,因变量是P(x | θ)。如果取θ = θ1,那么 P(x | θ1) 表示在 θ1 下,样本x出现的概率。
最大似然估计:指使似然函数最大。即 找到参数 θ 的一个估计值,使得当前样本x出现的可能性最大。
- 最大似然估计有一个前提:所有的采样都是独立同分布的,因此可以进行如下恒等变形
- 例子:
7.2 最大似然估计 与 经验风险 关系
当损失函数是对数损失函数时,经验风险最小化等价于极大似然估计。

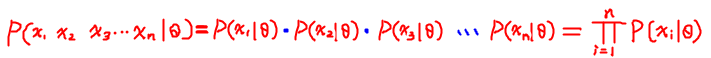








![[附源码]Node.js计算机毕业设计工会会员管理系统Express](https://img-blog.csdnimg.cn/ff8f6a2bc9d44ccabecadeeed1787a8b.png)