416. 分割等和子集
思路
本题是01背包的应用题
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
动态五部曲:
1.确定dp数组以及下标的含义
dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中物品重量是nums[i],物品价值也是nums[i]
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
2.确定递推公式
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]
3.dp数组如何初始化
本题初始化为0就可以了
4.确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
5.举例推导dp数组
dp[j]的数值一定是小于等于j的。

代码实现
class Solution {
public boolean canPartition(int[] nums) {
int n=nums.length;
int sum=0;
for(int num:nums){
sum+=num;
}
if(sum%2!=0){return false;}
int target=sum/2;
int[] dp=new int[target+1];
for(int i=0;i<n;i++){
for(int j=target;j>=nums[i];j--){//从后往前依次填充dp
//物品i的重量是nums[i],其价值也是nums[i]
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
if(dp[target]==target){return true;}
}
return false;
}
}1049. 最后一块石头的重量 II
本题与416题相似,就是要把石头分成重量尽量相等的两堆,相撞后剩下的石头重量尽可能小
物品重量和物品价值都是stone[i]
1.确定下标和dp数组含义
dp[j]表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。
2.确定递推公式
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3.dp数组如何初始化
题目中给出1 <= stones.length <= 30,1 <= stones[i] <= 1000,所以最大重量就是30 * 1000 。
而我们要求的target其实只是最大重量的一半,所以dp数组开到15000大小就可以了。当然我们也可以把石头遍历一遍,计算出石头总重量 然后除2,得到dp数组的大小
如何初始化dp[j]呢,因为重量都不会是负数,所以dp[j]都初始化为0就可以了
4.确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
5.举例推导dp数组
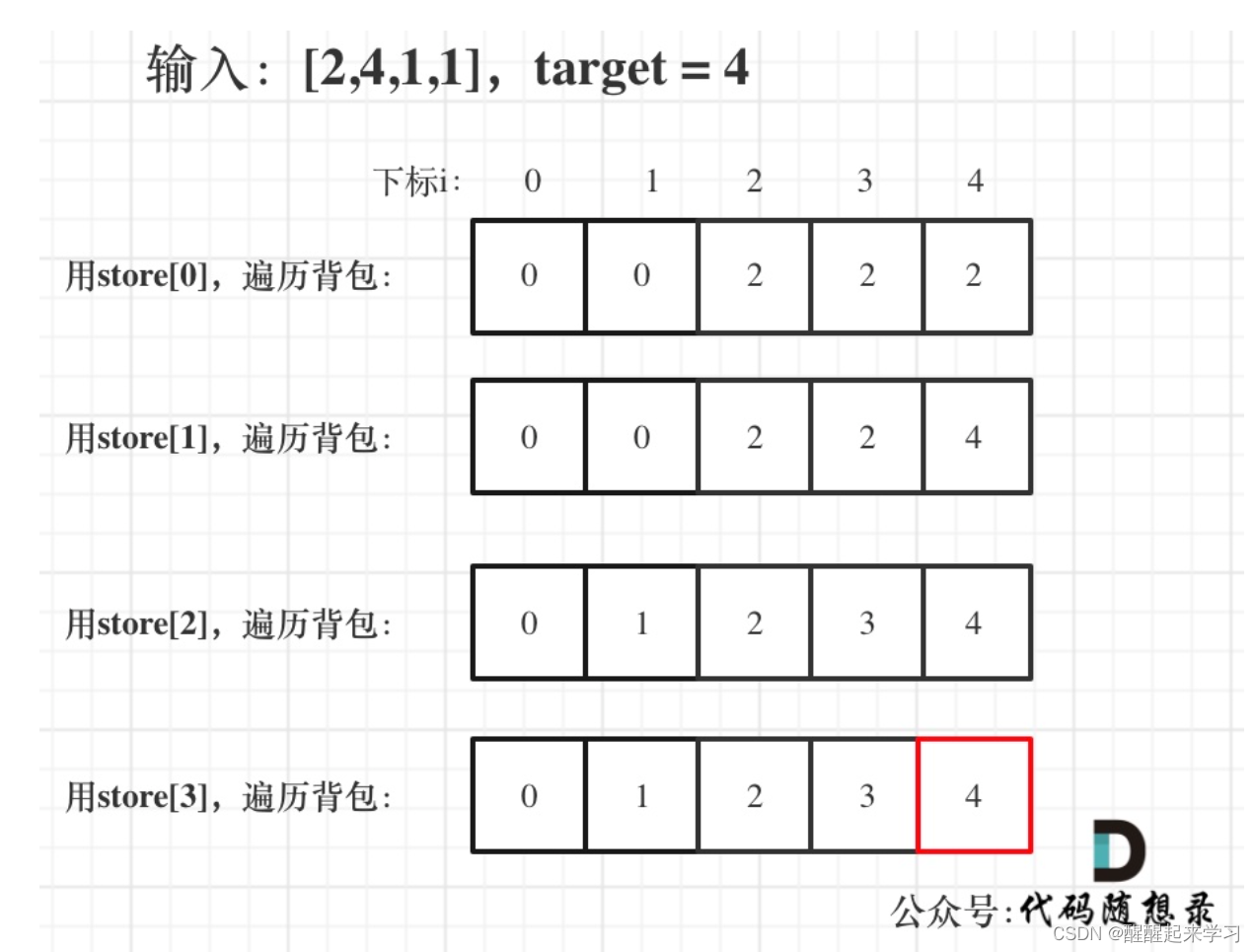
代码实现
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum=0;
for(int i:stones){
sum+=i;
}
int target=sum>>>1;
//初始化dp,容量为j的背包,最多可以背最大重量为dp[j]
int[] dp=new int[target+1];
for(int i=0;i<stones.length;i++){
//倒序
for(int j=target;j>=stones[i];j--){
dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return sum-dp[target]-dp[target];//dp[target]是一堆石头,sum-dp[target]是另一堆石头,二者相减就是相撞后的最小可能重量
//动态规划
//dp含义
//dp初始化
//递推公式
//模拟
}
}494.目标和
公式推导:
既然为target,那么就一定有 left组合 - right组合 = target。
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合。
1.确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法
2.确定递推公式
递推公式不理解
dp[j] += dp[j - nums[i]]
本题还是有点难度,大家也可以记住,在求装满背包有几种方法的情况下,递推公式一般为:
dp[j] += dp[j - nums[i]];
后面我们在讲解完全背包的时候,还会用到这个递推公式
3.dp数组如何初始化
从递推公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。所以我们应该初始化dp[0]=1
4.确定遍历顺序
nums放在外循环,target在内循环,且内循环倒序。
5.举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
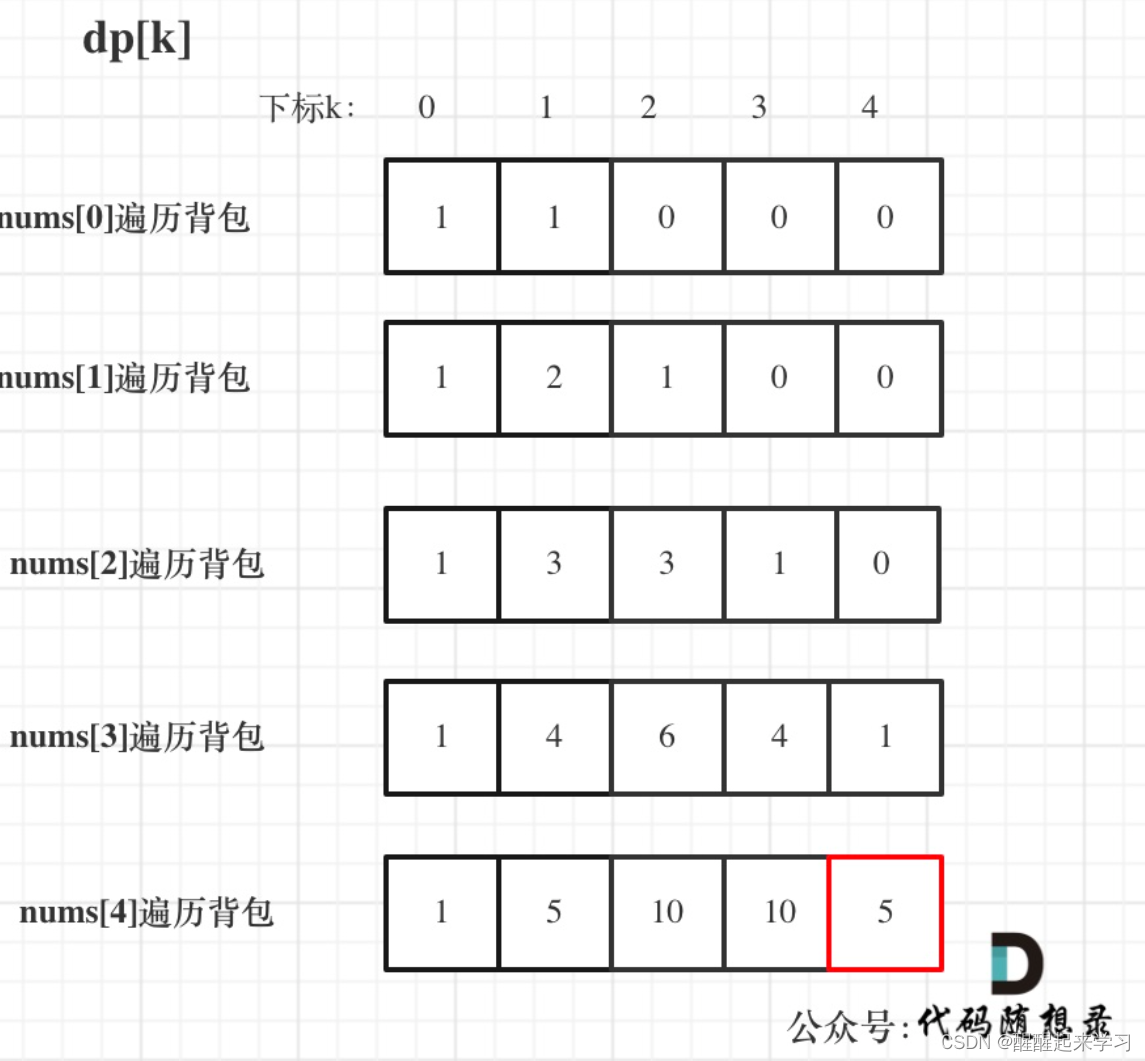
代码实现
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum=0;
for(int i=0;i<nums.length;i++){sum+=nums[i];}
//如果target过大,、
if(target<0&&sum<-target){return 0;}
if((target+sum)%2!=0){return 0;}//
int size=(target+sum)/2;
if(size<0){size=-size;}
int[] dp=new int[size+1];
dp[0]=1;
for(int i=0;i<nums.length;i++){
for(int j=size;j>=nums[i];j--){
dp[j]+=dp[j-nums[i]];
}
}
return dp[size];
}
}474.一和零(一窍不通)
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
理解成多重背包的同学主要是把m和n混淆为物品了,感觉这是不同数量的物品,所以以为是多重背包。
但本题其实是01背包问题!
开始动规五部曲:
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
2.确定递推公式
dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1)
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
3.dp数组如何初始化
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
4.确定遍历顺序
倒序遍历
本题物品就是strs里的字符串,背包容量就是题目描述中的m和n。
5.举例推导dp数组
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
最后dp数组的状态如下所示:
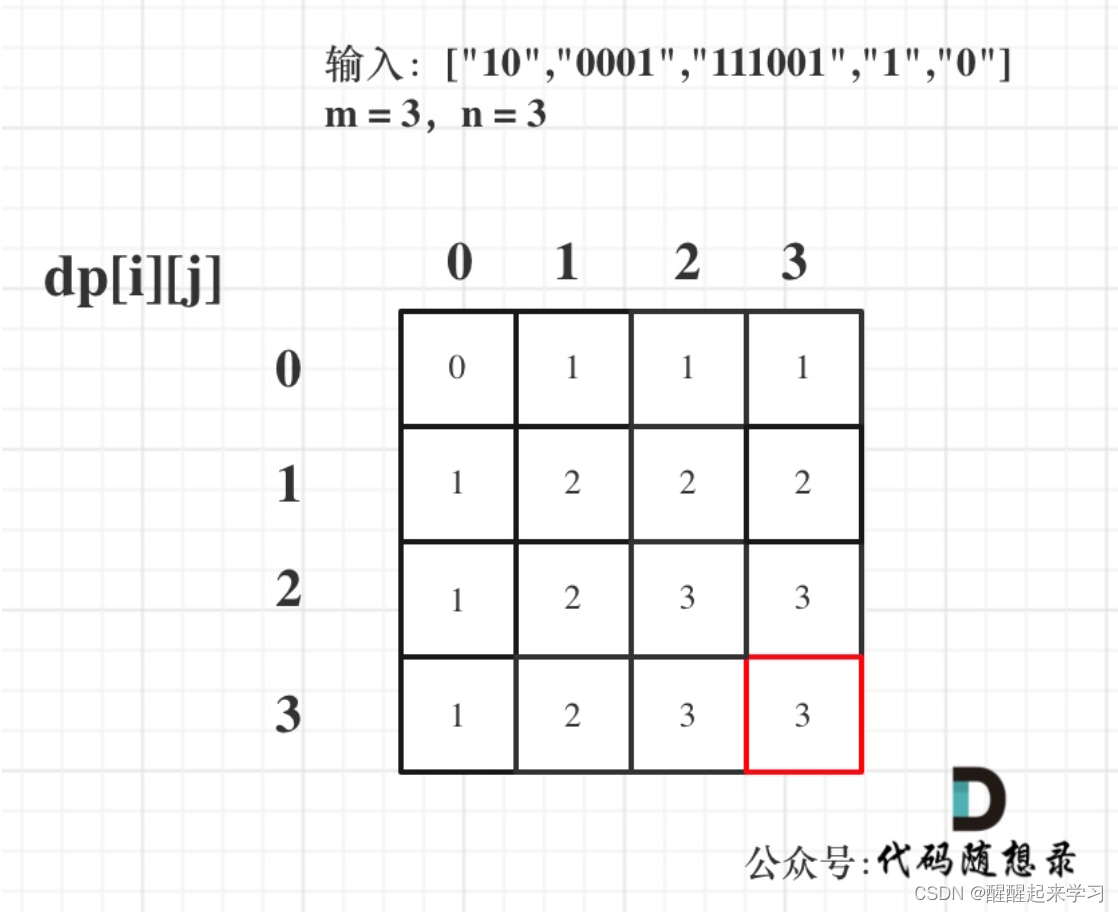
代码实现
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
//找出并返回 strs 的最大子集的长度,找出的该子集中最多有m个0和n个1.
//dp[i][j]表示i个0和j个1时的最大子集大小
int[][] dp=new int[m+1][n+1];
int oneNum,zeroNum;
for(String str:strs){
oneNum=0;//记录每个str的0 的个数
zeroNum=0;
for(char ch:str.toCharArray()){
if(ch=='0'){
zeroNum++;
}
else{oneNum++;}
}
for(int i=m;i>=zeroNum;i--){
for(int j=n;j>=oneNum;j--){
dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);//+1是累计数量加1
}
}
}
return dp[m][n];
}
}