11、非线性模型
当得到一个回归方程会,得到一条直线来拟合这个数据的统计规律,但是实际中用这样的简单直线很显然并不能拟合出统计规律,所谓线性回归比如两个变量之间关系就直接用一条直线来拟合,2个变量和一个1个变量的关系就用一个平面来拟合。在数学就是一个一元一次和多元一次函数的映射。非线性就是有多次,也就是说不再是一个直线了,可能是二次或者更高,也可以用三角函数来进行非线性变换。
11.1 读入数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from linear_regression import LinearRegression
data = pd.read_csv('../data/non-linear-regression-x-y.csv')
x = data['x'].values.reshape((data.shape[0], 1))
y = data['y'].values.reshape((data.shape[0], 1))
data.head(10)
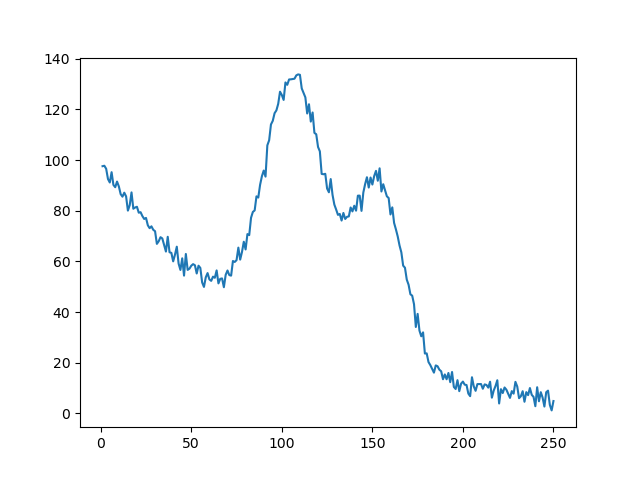
plt.plot(x, y)
plt.show()
- 导包
- 读入数据
- 得到x数据
- 得到y数据
- 取前10个
- 将x和y画图
打印结果:
11.2 多项式非线性变换函数
polynomial_degree是一个下面generate_polynomials这个多项式函数需要设置的参数
不同的参数产生的数据是怎样的呢?
如有一个数据[a,b]:
当degree=1时,kernel变换后的数据(仅为增加一个偏置项) 为:[1,a,b]
当degree=2时,kernel变换后的数据为:[1,a,b,
a
2
a^2
a2,ab,
b
2
b^2
b2]
当degree=3时,kernel变换后的数据为:[1,a,b,
a
2
a^2
a2,ab,
b
2
,
a
2
b
,
a
b
2
,
a
3
,
b
3
b^2,a^2b,ab^2,a^3,b^3
b2,a2b,ab2,a3,b3]
以此类推
import numpy as np
from .normalize import normalize
def generate_polynomials(dataset, polynomial_degree, normalize_data=False):
features_split = np.array_split(dataset, 2, axis=1)
dataset_1 = features_split[0]
dataset_2 = features_split[1]
(num_examples_1, num_features_1) = dataset_1.shape
(num_examples_2, num_features_2) = dataset_2.shape
if num_examples_1 != num_examples_2:
raise ValueError('Can not generate polynomials for two sets with different number of rows')
if num_features_1 == 0 and num_features_2 == 0:
raise ValueError('Can not generate polynomials for two sets with no columns')
if num_features_1 == 0:
dataset_1 = dataset_2
elif num_features_2 == 0:
dataset_2 = dataset_1
num_features = num_features_1 if num_features_1 < num_examples_2 else num_features_2
dataset_1 = dataset_1[:, :num_features]
dataset_2 = dataset_2[:, :num_features]
polynomials = np.empty((num_examples_1, 0))
for i in range(1, polynomial_degree + 1):
for j in range(i + 1):
polynomial_feature = (dataset_1 ** (i - j)) * (dataset_2 ** j)
polynomials = np.concatenate((polynomials, polynomial_feature), axis=1)
if normalize_data:
polynomials = normalize(polynomials)[0]
return polynomials
11.3 三角函数非线性变换函数
import numpy as np
def generate_sinusoids(dataset, sinusoid_degree):
num_examples = dataset.shape[0]
sinusoids = np.empty((num_examples, 0))
for degree in range(1, sinusoid_degree + 1):
sinusoid_features = np.sin(degree * dataset)
sinusoids = np.concatenate((sinusoids, sinusoid_features), axis=1)
return sinusoids
11.4 执行线性回归
num_iterations = 50000
learning_rate = 0.02
polynomial_degree = 15
sinusoid_degree = 15
normalize_data = True
linear_regression = LinearRegression(x, y, polynomial_degree, sinusoid_degree, normalize_data)
(theta, cost_history) = linear_regression.train( learning_rate, num_iterations)
print('开始损失: {:.2f}'.format(cost_history[0]))
print('结束损失: {:.2f}'.format(cost_history[-1]))
- 迭代次数
- 学习率
- 多项式次数
- 三角函数次数
- 类实例化成对象
- 执行train函数和之前一样
- 打印损失
打印结果:
开始损失: 2274.66
结束损失: 35.04
11.5 损失变化过程
theta_table = pd.DataFrame({'Model Parameters': theta.flatten()})
plt.plot(range(num_iterations), cost_history)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.title('Gradient Descent Progress')
plt.show()
这里和之前的过程是一样的,打印结果:
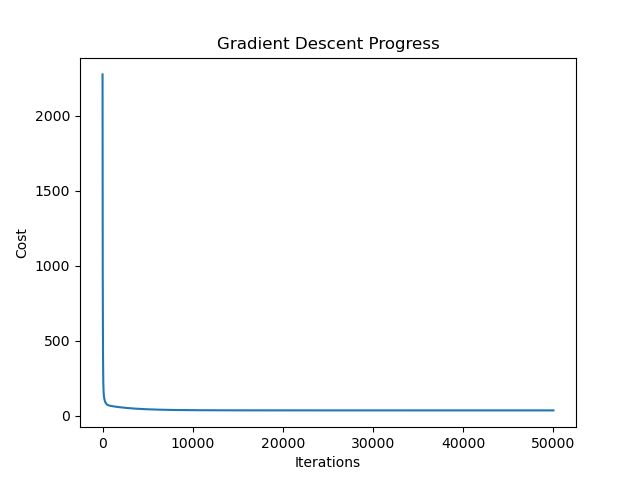
这里的损失在很早的时候就已经下降的很低了,因为次数设置的过大导致模型过拟合了
11.6 回归线
predictions_num = 1000
x_predictions = np.linspace(x.min(), x.max(), predictions_num).reshape(predictions_num, 1);
y_predictions = linear_regression.predict(x_predictions)
plt.scatter(x, y, label='Training Dataset')
plt.plot(x_predictions, y_predictions, 'r', label='Prediction')
plt.show()
这里的回归线实现过程还是和之前的一样,打印结果:
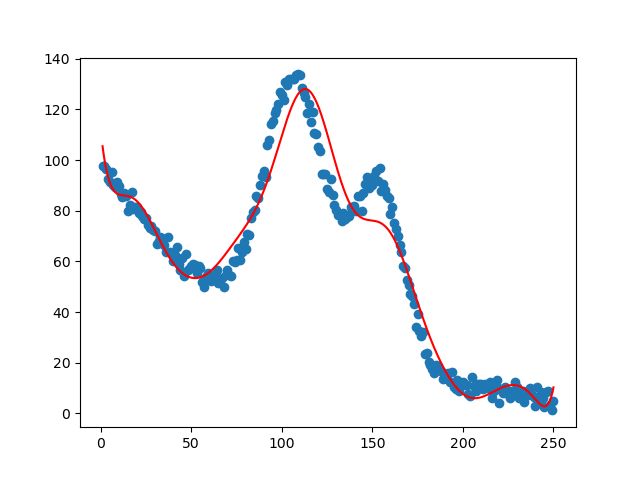
这就是用非线性回归实现的最后曲线拟合的结果