Dominosa/数邻（1） | C++ | 结构体和类

news2024/11/25 13:22:30

这里是目录

    • 一、背景介绍
    • 二、题目描述
    • 三、Dominosa 的技巧？
    • 四、编程思路
    • 五、完整代码
    • 六、补充

一、背景介绍

   你玩过骨牌吗？至少你一定听说过或者亲眼见过多米诺骨牌，而多米诺骨牌就发展自骨牌，这是一种古老的游戏，而我则是在b站上一个叫做”森纳映画“的up主那里学会骨牌的（但是我现在找不到这个视频了，当时好像是 21 年十月份左右），我甚至真的自己买了一副骨牌，带回家和我的好友家人一起玩这个游戏。

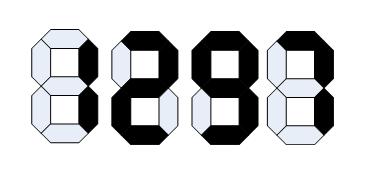
   骨牌是一种由两个方块组成的矩形，每个方块上都有点数，每个点数的大小都在 0 到 6 之间，任意两张骨牌的两个点数不会完全相同，一副标准的骨牌就有 7 × 8 2 = 28 \frac{7×8}{2} = 28 27×8​=28 张牌。

   如下图所示，例如左上角的这个骨牌由1和1组成，它下面的这个骨牌由2和1组成，任意两张骨牌上的点数不会相同。最小的数字是 0，最大的数字是 6。

在这里插入图片描述

（图源tb某商家）

   Dominosa，中文名称为数邻，是一种棋盘游戏，基于骨牌的排列和匹配来进行。它是从骨牌游戏中发展而来的，在骨牌的基础上添加了一些规则和难度。具体的游戏规则是：将一副骨牌放置在一个棋盘上，玩家需要根据这些固定数字推断出正确的骨牌排列。

   Dominosa 是一款非常有趣和具有挑战性的游戏。我是在 Linux 实训的小学期里，在虚拟机上接触到了这个小游戏。由于我本身玩过骨牌，同时对这种类型的数学游戏（比如数独之类的，我去年十月份也写过一篇用程序解决数独问题的文章）也很感兴趣，它们实在是令我着迷。 Dominosa 需要玩家运用逻辑思维和推理能力来解决问题。它的规则相对简单，但难度却很高，因为骨牌排列的可能性非常多。如果您喜欢逻辑游戏，并且想尝试一些挑战性的新游戏，那么 Dominosa 绝对值得一试！

   对于没有接触过骨牌的同学来说或许还不太能理解这个游戏，那么我们下面举一个具体的例子。下面是一个经典的 Dominosa 谜面。

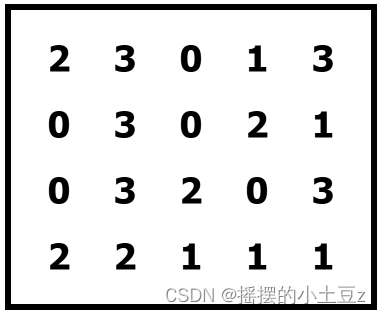
在这里插入图片描述

答案是这样的：

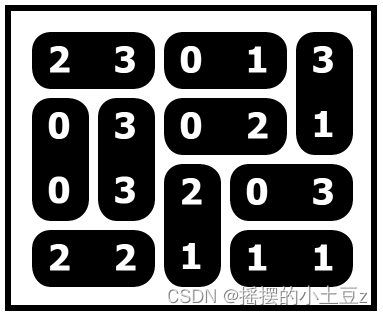
在这里插入图片描述

   可见，盘面上的数字被两两划分，且保证每个划分都互不重复。另外注意到，最小数字是 0，最大数字是 3，最大数字还可以是4、5、6等等，一般来说数字越大难度越大！

   我相信看完例子你一定懂了这个游戏的规则！现在，请你编写一个程序，对于给定的 Dominosa 谜面，能够自动判断是否有解，如果有解，还能够给出一个正确的解。

二、题目描述

输入一个未解的 Dominosa 谜面，输出它的结果。
Input
由两部分输入组成。第一部分只有一个正整数n，表示最大数字，第二部分有n+1行，每行n+2个正整数，表示谜面。
Output
谜题的解，如果两个数字能够组成一个骨牌，那么将它们的位置标记为相同的数字。标记方法可能不唯一，但是标记必须容易辨认。

下面是两个测试用例。

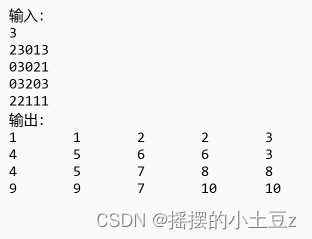
测试用例1
测试用例1

测试用例2
测试用例2

   这里补充解释输出为何是这样的：在程序的输出中，一样的数字表明它们的位置被划分在同一组骨牌中。例如测试用例 1 的输出对应的就是上面给过的例子。

三、Dominosa 的技巧？

   不管是直接百度还是去 b 站又或者是 CSDN 我能找到的技巧真是少之又少，别说技巧了资料都没多少，我顺便提一下 b 站上有一篇文章讲了一些技巧和方法。说实话，因为技巧真的不多而且限制颇多，关于 Dominosa 的技巧我只想说一句 “就这？”，好消息是倒也挺容易就能够编写程序让电脑帮我们计算出答案，毕竟我也就写了一个下午就写出来了。
   具体的技巧我就不提了，大家可以自己去玩一下感受一下，我的感觉就是这些技巧可有可无，不说你也能看出来，说了等于白说。而且最重要的是编写程序不会用到。

四、编程思路

1、读入 N N N， N N N 是谜面里的最大数字，一般不会超过 30，本题中为了方便输入我人为的设置为 N < 10 N<10 N<10。
2、接着读入 ( N + 1 ) ( N + 2 ) (N+1)(N+2) (N+1)(N+2) 个数据，表示谜面。
3、根据读入的数据初始化 DMNS，DMNS即Dominosa，是我的自定义类Dominosa的一个对象。
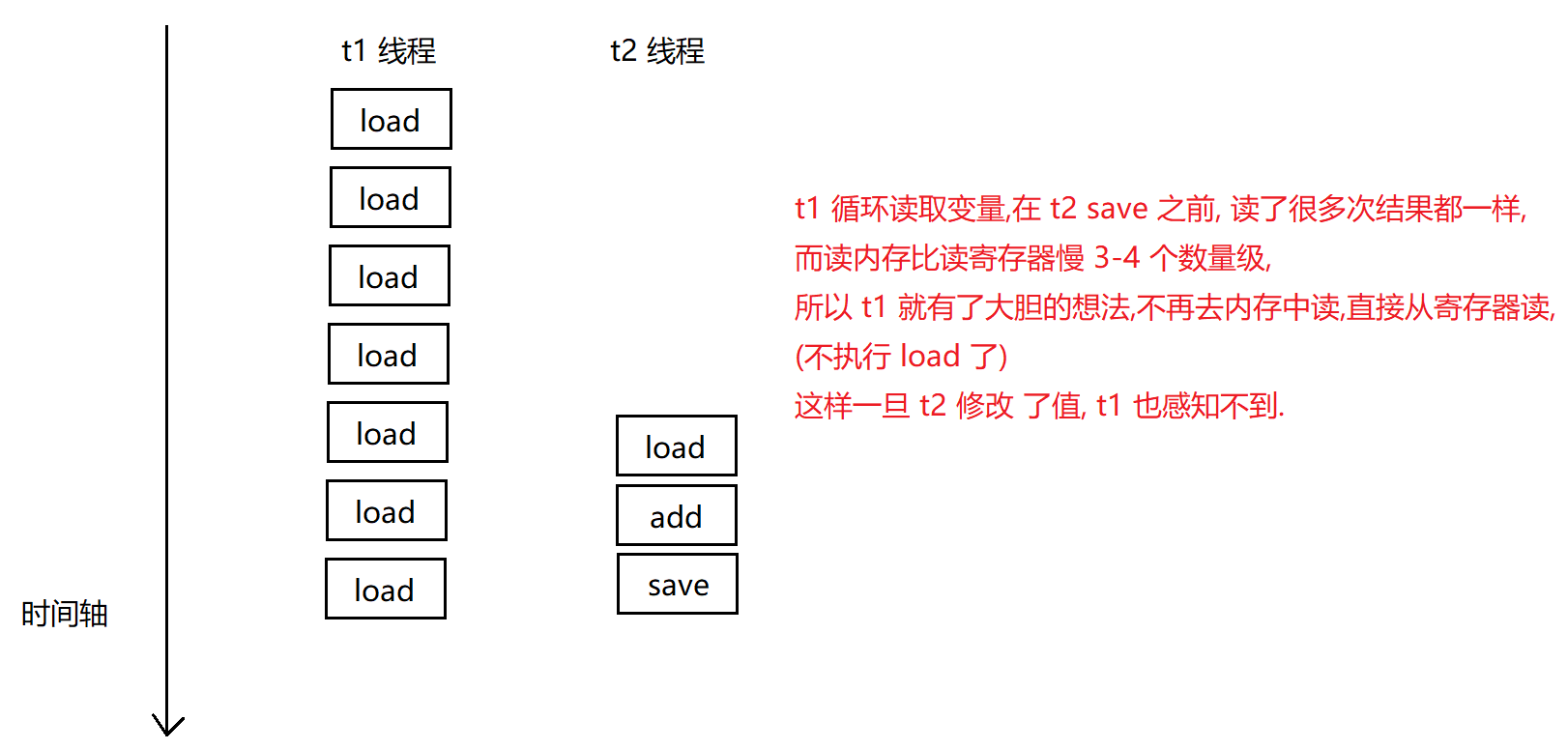
4、全面扫描 DMNS，更新 bridge.count。bridge 意为“桥”，我把骨牌看作是“连线”，如果两个相邻数字组成一个骨牌，我将它们直接连起来，这样连起来就很像是“搭桥”。统计“桥”的数量，如果某种“桥”的数量为1，说明这个骨牌是唯一的，在后续过程中我们当然要把它连起来。
5、全面扫描 DMNS 的每个格子，这里的每个格子都是一个我自定义的结构体。对于每一个格子，考虑如果它的四周只有一个格子可以相连，那它就一定与其相连；再考虑如果它的四周存在一座“桥”是唯一的，那么也一定可以相连。、、、这里我再举一个例子说明一下，例如这里可以连接 2 和 3 ，而其他任何地方都没有 2 和 3 相连，也就是说这里的 2 和 3 相连是唯一的，那么它们就一定是互连的，直接连起来就好。
6、全面更新 DMNS，更新每个格子的状态，我这里的格子是结构体。
7、重复步骤 4-6 若干

五、完整代码

具体过程见注释。

#include<bits/stdc++.h>
using namespace std;
int N = 30;							// N: 最大数字，不难计算出盘面的行数=N+1，列数=N+2
int sequence = 0;

// 定义单格
typedef struct {
	int number = -1;						// 表示当前格内的数字，初始是-1
	int con = 0;							// 表示当前格是否已建立连接，如果未连接，则为0，如果已连接，则为1
	int up=1, down=1, left=1, right=1;		// 标记当前格的上、下、左、右格子是否可能建立连接，如果可能则为1，如果不能则为0
	int sequ = 0;
} Single;

// 定义骨牌
typedef struct {
	int count;				// 编号：以6为例，00->0, 01->1, ..., 06->6, 11->7, ..., 16->12, 22->13, ..., 55->25, 56->26, 66->27；count是每种骨牌的数量
	bool used;				// used是骨牌是否已经出现过，若已经出现过则为true
} bridge;

int addd(int m){			// 一个求和的函数
	int s = 0;
	for (int i=1; i<m; i++) s+=i;
	return s;
}
// 根据骨牌上的两个数字将其转换为对应的b_id
int trans_numbers_bid(int number1, int number2) {	
	int addd(int);		
	int less = number1 < number2 ? number1 : number2, more = number1 + number2 - less;
	int b_id = less*N+more;
	if (less>1) b_id-=addd(less);
	return b_id;
}

// Dominosa棋盘类
class Dominosa{
public:
	Dominosa(){};				// 构造函数
	Dominosa(const Dominosa&);	// 拷贝函数
	~Dominosa(){};				// 析构函数
	Single lattice[31][32];		// 第i行第j列的格子位置为：k=21*i+j，理论支持的最大数字 N=30，但由于输入问题最大 N=9
	void init_connect();		// 初始化所有格子的up、down、left、right
	int sum_of_up_down_left_right(int m, int n); // 计算上下左右的和
};
Dominosa:: Dominosa(const Dominosa& dd) {
	for (int i=0; i<21; i++) {
		for (int j=0; j<22; j++) {
			this->lattice[i][j] = dd.lattice[i][j];
		}
	}
}
void Dominosa:: init_connect(){
	// 初始化所有格子的up、down、left、right
	for (int j=0; j<N+2; j++) {
		lattice[0][j].up = 0;
		lattice[N][j].down = 0;
	}
	for (int i=0; i<N+1; i++) {
		lattice[i][0].left = 0;
		lattice[i][N+1].right = 0;
	}
}
// 计算当前格与上下左右可能性的和，m是行数，n是列数
int Dominosa:: sum_of_up_down_left_right(int m, int n){
	// 如果是边缘格子，单独考虑
	if (m==0) {
		if (n==0) {
			return lattice[m][n].right+lattice[m][n].down;
		}
		else if (n==N+1) {
			return lattice[m][n].left+lattice[m][n].down;
		}
		else {
			return lattice[m][n].left+lattice[m][n].right+lattice[m][n].down;
		}
	}
	else if (m==N) {
		if (n==0) {
			return lattice[m][n].up+lattice[m][n].right;
		}
		else if (n==N+1) {
			return lattice[m][n].left+lattice[m][n].up;
		}
		else {
			return lattice[m][n].left+lattice[m][n].right+lattice[m][n].up;
		}
	}
	else {
		if (n==0) {
			return lattice[m][n].right+lattice[m][n].up+lattice[m][n].down;
		}
		else if (n==N+1) {
			return lattice[m][n].left+lattice[m][n].up+lattice[m][n].down;
		}
		else {
			return lattice[m][n].up+lattice[m][n].down+lattice[m][n].left+lattice[m][n].right;
		}
	}
}







Dominosa DMNS;				// 基础盘面DMNS
int main() {
	
	int addd(int);
	int trans_numbers_bid(int, int);

	// 初始化谜面
	DMNS.init_connect();
	sequence++;

    freopen("input.txt","r",stdin);		// 谜面放在 input.txt 中
    //读入待解盘面D
	scanf("%d\n", &N);
	char c;
	for (int i=0; i<N+1; i++) {
		for (int j=0; j<N+2; j++) {
			scanf("%c", &c);
			DMNS.lattice[i][j].number = c - '0';
			DMNS.lattice[i][j].con = 0;
		}
		scanf("%*c");
	}
	// 初始化bridge
	int count_of_bridges = (N+1)*(N+2)/2;
	bridge b[count_of_bridges];
	for (int i=0; i<count_of_bridges; i++) {
		b[i].used = false;
	}

	bool update = true;
	while (update) {
		update = false;
		
		// 初始化bridge.count
		for (int i=0; i<count_of_bridges; i++) {
			b[i].count = 0;
		}
		// 全面扫描DMNS，更新bridge.count
		// 先横向扫描一遍，更新bridge.count
		for (int i=0; i<N+1; i++) {
			for (int j=0; j<N+1; j++) {
				if (DMNS.lattice[i][j].con==0 && DMNS.lattice[i][j+1].con==0) {
					b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].count++;
				}
			}
		}
		// 再纵向扫描一遍，更新bridge.count
		for (int i=0; i<N; i++) {
			for (int j=0; j<N+2; j++) {
				if (DMNS.lattice[i][j].con==0 && DMNS.lattice[i+1][j].con==0) {
					b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].count++;
				}
			}
		}

		// 从左向右扫描一遍，并尝试向右建立连接
		for (int i=0; i<N+1; i++) {
			for (int j=0; j<N+1; j++) {
				if (DMNS.lattice[i][j].con==0 && DMNS.lattice[i][j+1].con==0) {
					if (DMNS.sum_of_up_down_left_right(i, j)==1 && DMNS.lattice[i][j].right==1) {
						DMNS.lattice[i][j].con = 1;
						DMNS.lattice[i][j].sequ = sequence;
						DMNS.lattice[i][j+1].con = 1;
						DMNS.lattice[i][j+1].sequ = sequence;
						sequence++;
						b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used = true;
						update = true;
					}
					if (b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used==false
						&& b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].count==1) {
							DMNS.lattice[i][j].con = 1;
							DMNS.lattice[i][j].sequ = sequence;
							DMNS.lattice[i][j+1].con = 1;
							DMNS.lattice[i][j+1].sequ = sequence;
							sequence++;
							b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used = true;
							update = true;
					}
				}
			}
		}
		// 从右向左扫描一遍，并尝试向左建立连接
		for (int i=0; i<N+1; i++) {
			for (int j=1; j<N+2; j++) {
				if (DMNS.lattice[i][j].con==0 && DMNS.lattice[i][j-1].con==0) {
					if (DMNS.sum_of_up_down_left_right(i, j)==1 && DMNS.lattice[i][j].left==1) {
						DMNS.lattice[i][j].con = 1;
						DMNS.lattice[i][j].sequ = sequence;
						DMNS.lattice[i][j-1].con = 1;
						DMNS.lattice[i][j-1].sequ = sequence;
						sequence++;
						b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used = true;
						update = true;
					}
					if (b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used==false
						&& b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].count==1) {
							DMNS.lattice[i][j].con = 1;
							DMNS.lattice[i][j].sequ = sequence;
							DMNS.lattice[i][j-1].con = 1;
							DMNS.lattice[i][j-1].sequ = sequence;
							sequence++;
							b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used = true;
							update = true;
					}
				}
			}
		}
		// 从上向下扫描一遍，并尝试向下建立连接
		for (int i=0; i<N; i++) {
			for (int j=0; j<N+2; j++) {
				if (DMNS.lattice[i][j].con==0 && DMNS.lattice[i+1][j].con==0) {
					if (DMNS.sum_of_up_down_left_right(i, j)==1 && DMNS.lattice[i][j].down==1) {
						DMNS.lattice[i][j].con = 1;
						DMNS.lattice[i][j].sequ = sequence;
						DMNS.lattice[i+1][j].con = 1;
						DMNS.lattice[i+1][j].sequ = sequence;
						sequence++;
						b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used = true;
						update = true;
					}
					if (b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used==false
						&& b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].count==1) {
							DMNS.lattice[i][j].con = 1;
							DMNS.lattice[i][j].sequ = sequence;
							DMNS.lattice[i+1][j].con = 1;
							DMNS.lattice[i+1][j].sequ = sequence;
							sequence++;
							b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used = true;
							update = true;
					}
				}
			}
		}
		// 从下向上扫描一遍，并尝试向上建立连接
		for (int i=1; i<N+1; i++) {
			for (int j=0; j<N+2; j++) {
				if (DMNS.lattice[i][j].con==0 && DMNS.lattice[i-1][j].con==0) {
					if (DMNS.sum_of_up_down_left_right(i, j)==1 && DMNS.lattice[i][j].up==1) {
						DMNS.lattice[i][j].con = 1;
						DMNS.lattice[i][j].sequ = sequence;
						DMNS.lattice[i-1][j].con = 1;
						DMNS.lattice[i-1][j].sequ = sequence;
						sequence++;
						b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used = true;
						update = true;
					}
					if (b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used==false
						&& b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].count==1) {
							DMNS.lattice[i][j].con = 1;
							DMNS.lattice[i][j].sequ = sequence;
							DMNS.lattice[i-1][j].con = 1;
							DMNS.lattice[i-1][j].sequ = sequence;
							sequence++;
							b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used = true;
							update = true;
					}
				}
			}
		}

		// 全面更新DMNS的每个con=0格子的up、down、left、right状态
		// 如果相邻的格子的con=1，则将其方向设置为0
		// 如果相邻的格子的con=0，但bridge.used=true，也要将其方向设置为0
		{
			int i=0;
			{
				int j=0;
				if (DMNS.lattice[i][j].con==0) {
					if (DMNS.lattice[i][j+1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used==true ) {
						DMNS.lattice[i][j].right = 0;
					}
					if (DMNS.lattice[i+1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used==true ) {
						DMNS.lattice[i][j].down = 0;
					}
				}
				for (j=1; j<N+1; j++) {
					if (DMNS.lattice[i][j].con==0) {
						if (DMNS.lattice[i][j-1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used==true ) {
							DMNS.lattice[i][j].left = 0;
						}
						if (DMNS.lattice[i][j+1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used==true ) {
							DMNS.lattice[i][j].right = 0;
						}
						if (DMNS.lattice[i+1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used==true ) {
							DMNS.lattice[i][j].down = 0;
						}
					}
				}
				j = N+1;
				if (DMNS.lattice[i][j].con==0) {
					if (DMNS.lattice[i][j-1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used==true ) {
						DMNS.lattice[i][j].left = 0;
					}
					if (DMNS.lattice[i+1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used==true ) {
						DMNS.lattice[i][j].down = 0;
					}
				}
			}

			{
				for (i=1; i<N; i++) {
					int j=0;
					if (DMNS.lattice[i][j].con==0) {
						if (DMNS.lattice[i][j+1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used==true ) {
							DMNS.lattice[i][j].right = 0;
						}
						if (DMNS.lattice[i-1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used==true ) {
							DMNS.lattice[i][j].up = 0;
						}
						if (DMNS.lattice[i+1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used==true ) {
							DMNS.lattice[i][j].down = 0;
						}
					}
					for (j=1; j<N+1; j++) {
						if (DMNS.lattice[i][j].con==0) {
							if (DMNS.lattice[i][j-1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used==true ) {
								DMNS.lattice[i][j].left = 0;
							}
							if (DMNS.lattice[i][j+1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used==true ) {
								DMNS.lattice[i][j].right = 0;
							}
							if (DMNS.lattice[i-1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used==true ) {
								DMNS.lattice[i][j].up = 0;
							}
							if (DMNS.lattice[i+1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used==true ) {
								DMNS.lattice[i][j].down = 0;
							}
						}
					}
					j = N+1;
					if (DMNS.lattice[i][j].con==0) {
						if (DMNS.lattice[i][j-1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used==true ) {
							DMNS.lattice[i][j].left = 0;
						}
						if (DMNS.lattice[i-1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used==true ) {
							DMNS.lattice[i][j].up = 0;
						}
						if (DMNS.lattice[i+1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i+1][j].number)].used==true ) {
							DMNS.lattice[i][j].down = 0;
						}
					}
				}
			}

			{
				i = N;
				int j=0;
				if (DMNS.lattice[i][j].con==0) {
					if (DMNS.lattice[i][j+1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used==true ) {
						DMNS.lattice[i][j].right = 0;
					}
					if (DMNS.lattice[i-1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used==true ) {
						DMNS.lattice[i][j].up = 0;
					}
				}
				for (j=1; j<N+1; j++) {
					if (DMNS.lattice[i][j].con==0) {
						if (DMNS.lattice[i][j-1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used==true ) {
							DMNS.lattice[i][j].left = 0;
						}
						if (DMNS.lattice[i][j+1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j+1].number)].used==true ) {
							DMNS.lattice[i][j].right = 0;
						}
						if (DMNS.lattice[i-1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used==true ) {
							DMNS.lattice[i][j].up = 0;
						}
					}
				}
				j = N+1;
				if (DMNS.lattice[i][j].con==0) {
					if (DMNS.lattice[i][j-1].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i][j-1].number)].used==true ) {
						DMNS.lattice[i][j].left = 0;
					}
					if (DMNS.lattice[i-1][j].con==1 || b[trans_numbers_bid(DMNS.lattice[i][j].number, DMNS.lattice[i-1][j].number)].used==true ) {
						DMNS.lattice[i][j].up = 0;
					}
				}
			}
		}
	
		// // 输出每次更新的结果
		// for (int i=0; i<N+1; i++) {
		// 	for (int j=0; j<N+2; j++) {
		// 		cout << setw(4) << DMNS.lattice[i][j].sequ;
		// 	}
		// 	cout << endl;
		// }
		// cout << endl;

		// cout << "Debug: 输出每个格子的up down left right状态" << endl;
		// for (int i=0; i<N+1; i++) {
		// 	cout << "i = " << i << endl;
		// 	for (int j=0; j<N+2; j++) {
		// 		cout << DMNS.lattice[i][j].up << " " << DMNS.lattice[i][j].down << " " << DMNS.lattice[i][j].left << " " << DMNS.lattice[i][j].right << endl;
		// 	}
		// }
		// cout << endl;

		// cout << "Debug: 输出所有bridge的连接状态" << endl;
		// for (int i=0; i<=N; i++) {
		// 	for (int j=i; j<=N; j++) {
		// 		cout << i << j << ": " << b[trans_numbers_bid(i, j)].used << " ";
		// 	}
		// }
		// cout << endl;
	}
	
	// 输出最终的结果
	for (int i=0; i<N+1; i++) {
		for (int j=0; j<N+2; j++) {
			cout << setw(4) << DMNS.lattice[i][j].sequ;
		}
		cout << endl;
	}
	
    return 0;
}

还好啦，也就 422 行而已，一个下午就写完了。

   注意输入一定要按照我的格式来，仅支持 N < 10 N<10 N<10 的情形。如果你想要让 N ≥ 10 N\ge10 N≥10，那么就要在输入中添加空格，相应地也修改一下程序中的输入。你也可以修改一下，让输出在一个文件里面。

   最初，我想履行上次的承诺用python写，但是我不知道python是没有还是不会，我不会搞结构体，我还挺喜欢结构体这个东西的，所以还是用回了C++。

六、补充

首先是两个测试用例的情况，对于测试用例2，还算比较成功，它顺利地给出了答案。在程序的帮助下，包括我花费在输入上的时间，一个预计耗时半个小时的题目我只用了两分钟半就做出来了。
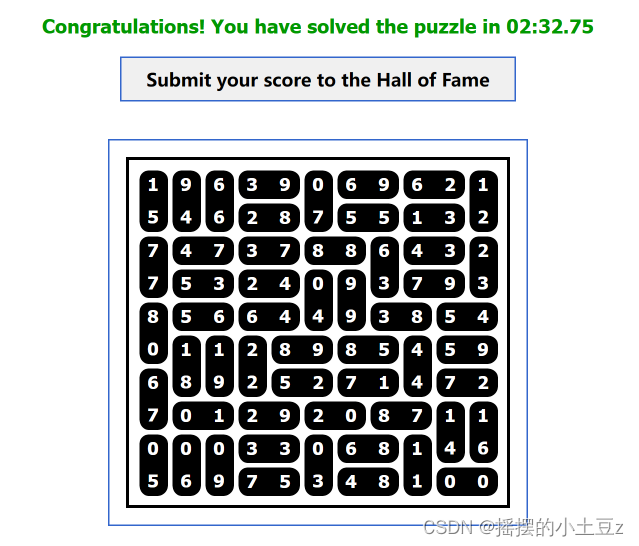
在这里插入图片描述

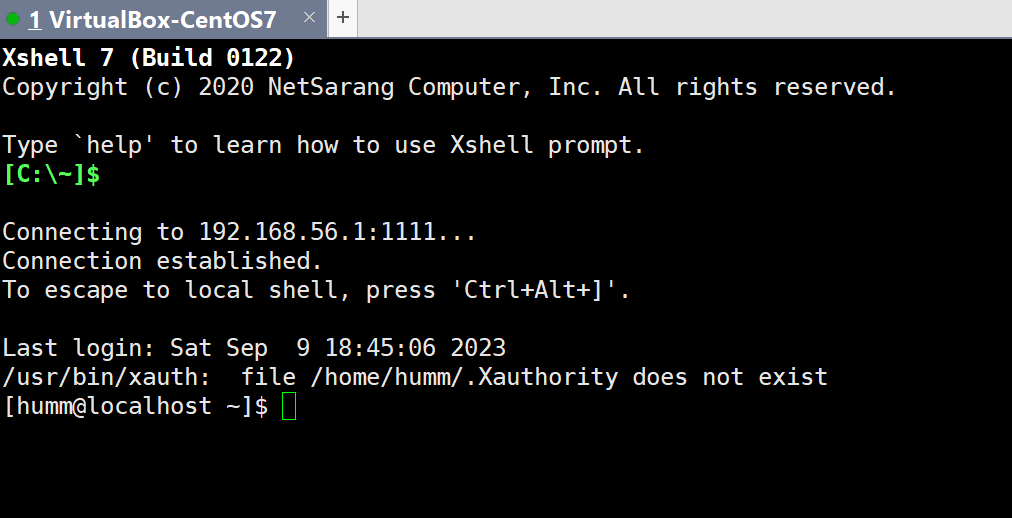
但是对于测试用例1，我很遗憾地告知，对于极端情况下这个程序确实是解不出来的，它运行的结果是这样的：

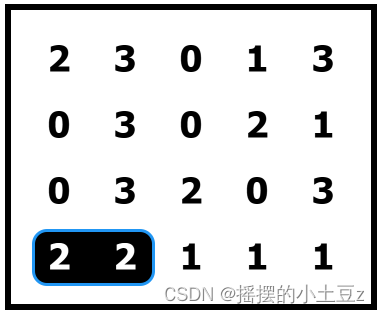
在这里插入图片描述

对应下面的情况：

在这里插入图片描述

可见这个程序是存在缺陷的，有时候需要“主动”去试错，就像数独那样。

是的，就像数独那样，我的意思是，可以像上次那样用 BFS 做，这也就是下一篇文章的内容了。我们下一篇文章见，顺便巩固一下 BFS。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/993562.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Linux】VirtualBox安装Centos7

【Linux】VirtualBox安装Centos7

文章目录 下载并安装VirtualBox下载Centos镜像VirtualBox设置管理->全局设定&#xff1a;设定虚拟机默认安装路径工具->网络管理器&#xff1a;添加NetWork网络配置 VirtualBox安装CentOS7新建虚拟机&#xff0c;指定安装目录及名称&#xff0c;点击下一步指定虚拟机内存…
阅读更多...
记录征战Mini开发板从无到有（二）

记录征战Mini开发板从无到有（二）

接上一篇&#xff0c;原理图设计完成后&#xff0c;就要画PCB图了。因为PCB直接影响板子的性能&#xff0c;所以决定花钱找一博科技的资深工程师来布板。布板效果非常好&#xff0c;细节处理得很到位&#xff0c;真的是专业的人干专业的事&#xff0c;话不多说&#xff0c;来欣…
阅读更多...
无涯教程-JavaScript - OCT2BIN函数

无涯教程-JavaScript - OCT2BIN函数

描述 OCT2BIN函数将八进制数转换为二进制数。 语法 OCT2BIN (number, [places])争论 Argument描述Required/OptionalNumber 您要转换的八进制数。 数字不能超过10个字符。数字的最高有效位是符号位。其余的29位是幅度位。 负数使用二进制补码表示。 RequiredPlaces 要使用的…
阅读更多...
python library reference

python library reference

文章目录 1. 标准库2. Python标准库介绍3. 示例 1. 标准库 https://docs.python.org/zh-cn/3/library/ https://pypi.org/ https://pypi.org/search/ 2. Python标准库介绍 Python 语言参考手册 描述了 Python 语言的具体语法和语义&#xff0c;这份库参考则介绍了与 Pytho…
阅读更多...
【多线程】线程安全 问题

【多线程】线程安全 问题

线程安全 问题 一. 线程不安全的典型例子二. 线程安全的概念三. 线程不安全的原因1. 线程调度的抢占式执行2. 修改共享数据3. 原子性4. 内存可见性5. 指令重排序 一. 线程不安全的典型例子 class ThreadDemo {static class Counter {public int count 0;void increase() {cou…
阅读更多...
openpnp - 二手西门子电动飞达的测试

openpnp - 二手西门子电动飞达的测试

文章目录 二手西门子电动飞达的初步测试概述飞达正常的判断标准先挑出一个手工控制好使的二手飞达用于测试.推料的手工检测扒皮的手工检测飞达测试的接线通讯的测试用串口助手测试通讯先看看是否发送给飞达的管脚是自己接的那个查看所有可以用到的上位机通讯命令M115 - 打印固件…
阅读更多...
蓝桥杯官网练习题（颠倒的价牌）

蓝桥杯官网练习题（颠倒的价牌）

题目描述 本题为填空题&#xff0c;只需要算出结果后&#xff0c;在代码中使用输出语句将所填结果输出即可。 小李的店里专卖其它店中下架的样品电视机&#xff0c;可称为&#xff1a;样品电视专卖店。 其标价都是 4 位数字&#xff08;即千元不等&#xff09;。 小李为了标…
阅读更多...
BWMT的思考

BWMT的思考

从bw4开始&#xff0c;sap把建模的功能从系统的rsa1移除&#xff0c;改成BWMT的客户端。以前对java开发的eclipse不是很喜欢&#xff0c;总有点排斥。今天突然好像明白sap为啥要这样做&#xff1f; 1 最重要的是减少数据库的数据量和系统的负荷。把这种开发工作的程序和功能放在…
阅读更多...
基于微信小程序美食菜品预订点餐预约系统uniapp+vue

基于微信小程序美食菜品预订点餐预约系统uniapp+vue

点餐预约系统主要是为了提高用户的工作效率和更方便快捷的满足用户&#xff0c;更好存储所有数据信息及快速方便的检索功能&#xff0c;对点餐预约系统的各个模块是通过许多今天的发达点餐预约系统做出合理的分析来确定考虑用户的可操作性&#xff0c;遵循开发的系统优化的原则…
阅读更多...
Games101作业5解读

Games101作业5解读

文章目录 整体思路阅读Render 整体思路阅读 Scene scene(1280, 960);auto sph1 std::make_unique<Sphere>(Vector3f(-1, 0, -12), 2);sph1->materialType DIFFUSE_AND_GLOSSY;sph1->diffuseColor Vector3f(0.6, 0.7, 0.8);auto sph2 std::make_unique<Spher…
阅读更多...
530. 二叉搜索树的最小绝对差

530. 二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root &#xff0c;返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数&#xff0c;其数值等于两值之差的绝对值。 示例 1&#xff1a; 输入&#xff1a;root [4,2,6,1,3] 输出&#xff1a;1示例 2&#xff1a; 输入&#xff1a;root [1,…
阅读更多...
Windows创建sqlite3的lib库

Windows创建sqlite3的lib库

1、下载相关文件 SQLite Download Page这是sqlite的官网下载地址&#xff0c;需要下载三个文件&#xff1a; 下载后解压得到代码文件&#xff1a; dll选择一个就行&#xff0c;x86或者x64根据自己的需要下载。 dll得到动态库文件&#xff1a; tools得到exe文件&#xff1a; 2…
阅读更多...
LabVIEW开发人体动态电位器设计及应用

LabVIEW开发人体动态电位器设计及应用

LabVIEW开发人体动态电位器设计及应用 随着集成电路产业的快速发展&#xff0c;电子设备的集成密度显著提高。电子设备的防静电能力变差&#xff0c;电子设备对静电放电的易感性也更严重。人类是各种科研活动的主要焦点&#xff0c;也是静电防护中的主要危险源之一。如果一个人…
阅读更多...
【C++进阶】：AVL树(平衡因子)

【C++进阶】：AVL树(平衡因子)

AVL树 一.概念二.插入1.搜索二叉树2.平衡因子 三.旋转1.更新平衡因子2.旋转1.左单旋2.右单旋3.先右旋再左旋4.先左旋再右旋 四.完整代码 一.概念 二叉搜索树虽可以缩短查找的效率&#xff0c;但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元…
阅读更多...
CMS指纹识别

CMS指纹识别

一.什么是指纹识别 常见cms系统 通过关键特征&#xff0c;识别出目标的CMS系统&#xff0c;服务器&#xff0c;开发语言&#xff0c;操作系统&#xff0c;CDN&#xff0c;WAF的类别版本等等 1.识别对象 1.CMS信息&#xff1a;比如Discuz,织梦&#xff0c;帝国CMS&#xff0…
阅读更多...
MongoDB ubuntu 上安装 MongoDB7.0 附带配置文件说明

MongoDB ubuntu 上安装 MongoDB7.0 附带配置文件说明

开头还是介绍一下群&#xff0c;如果感兴趣PolarDB ,MongoDB ,MySQL ,PostgreSQL ,Redis &#xff0c;Oracle ,Oceanbase 等有问题&#xff0c;有需求都可以加群群内有各大数据库行业大咖&#xff0c;CTO&#xff0c;可以解决你的问题。加群请加微信号 liuaustin3 &#xff08;…
阅读更多...
TDesign的input标签

TDesign的input标签

目录 一、 新建页面01-todolist 二、 t-input标签、t-button标签 2.1 t-input标签 2.1.1 01-todolist.wxml页面 2.2 01-todolist.json页面 2.3 01-todolist.js页面 2.4 01-todolist.wxss页面 2.2 t-button标签 示例1&#xff1a; 示例2 &#xff1a; 一、 新建页面0…
阅读更多...
【LeetCode题目详解】第九章 动态规划part08 139.单词拆分 （day46补）

【LeetCode题目详解】第九章 动态规划part08 139.单词拆分 （day46补）

本文章代码以c为例&#xff01; 一、力扣第139题&#xff1a;单词拆分 题目&#xff1a; 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意&#xff1a;不要求字典中出现的单词全部都使用&#xff0c;并且字典…
阅读更多...
linux系统中rootfs根文件系统制作及挂载基本操作

linux系统中rootfs根文件系统制作及挂载基本操作

​今天给大家介绍一下rootfs根文件系统制作和挂载方式&#xff0c;希望这篇文章对大家有所帮助。 本章主要是对rootfs根文件系统制作和挂载方式进行详细讲解。 Linux“三巨头”已经完成了2个了&#xff0c;就剩最后一个 rootfs(根文件系统)了&#xff0c;本章我们就来学习一下…
阅读更多...
日常开发小汇总（4）空对象创造

日常开发小汇总（4）空对象创造

创建空对象的目的其实是想要一个干净的对象&#xff0c;最直接的方式是将对象的隐式原型干掉&#xff0c;如 下图就会得到一个干净的对象&#xff0c;但是这种方式不推荐&#xff0c;不要直接操作__proto__ 方式一 Object.create(null) 方法二 Object.setPrototypeOf(对象&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023