目录
编辑
一,被围绕的区域
1.题意
2.解释
3.题目接口
4.解题思路及代码
二,太平洋大西洋流水问题
1.题意
2.解释
3.题目接口
4.解题思路及代码
一,被围绕的区域
1.题意
给你一个
m x n的矩阵board,由若干字符'X'和'O',找到所有被'X'围绕的区域,并将这些区域里所有的'O'用'X'填充。
2.解释
如下图所示:
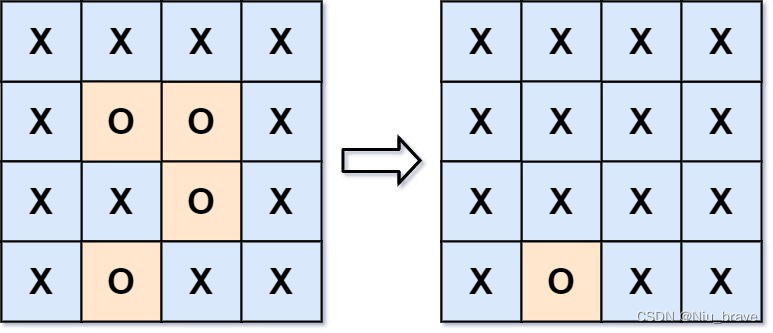
该图中只有最底下的字母O没有被改为字符X,因为它下边没有被字符X给围绕,所以这个字符O不用被修改,但是其它几个O是连在一起的并且是被字符X给围绕起来的所以就会被修改为字符X。
3.题目接口
class Solution {
public:
void solve(vector<vector<char>>& board) {
}
};4.解题思路及代码
这道题其实是比较考验思维的,因为如果我们采用直接遍历的方法来解决的话会很吃力,因为我们要处理的情况太多了。这个时候我们就可以采取逆向的思维解决这道题了。这道题,要我们找到符合条件的可以改为字符X的字符O,这是正向的思维。逆向的思维便是找到不符合条件的O然后将这些O给标记一下不能改为X。具体的代码如下:
class Solution { public: int m,n; int dx[4] = {0,0,1,-1},dy[4] = {1,-1,0,0}; void solve(vector<vector<char>>& board) { m = board.size(); n = board[0].size(); //先从边界开始找到不符合条件的字符O改为一个特定的符号'.' for(int i = 0;i<m;i++) { if(board[i][0] == 'O') { dfs(board,i,0); } if(board[i][n-1] == 'O') { dfs(board,i,n-1); } } for(int j = 0;j<n;j++) { if(board[0][j]=='O') { dfs(board,0,j); } if(board[m-1][j]=='O') { dfs(board,m-1,j); } } //遍历全员,将标记过的字符改为O,把字符为O的改为X for(int i = 0;i<m;i++) { for(int j = 0;j<n;j++) { if(board[i][j] == '.') { board[i][j] = 'O'; } else if(board[i][j]=='O') { board[i][j] = 'X'; } } } } void dfs(vector<vector<char>>&board,int i,int j) { board[i][j] = '.'; for(int k = 0;k<4;k++) { int x = i+dx[k],y = j+dy[k]; if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='O') { dfs(board,x,y); } } } };
二,太平洋大西洋流水问题
1.题意
有一个
m × n的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。这个岛被分割成一个由若干方形单元格组成的网格。给定一个
m x n的整数矩阵heights,heights[r][c]表示坐标(r, c)上单元格 高于海平面的高度 。岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标
result的 2D 列表 ,其中result[i] = [ri, ci]表示雨水从单元格(ri, ci)流动 既可流向太平洋也可流向大西洋 。
2.解释
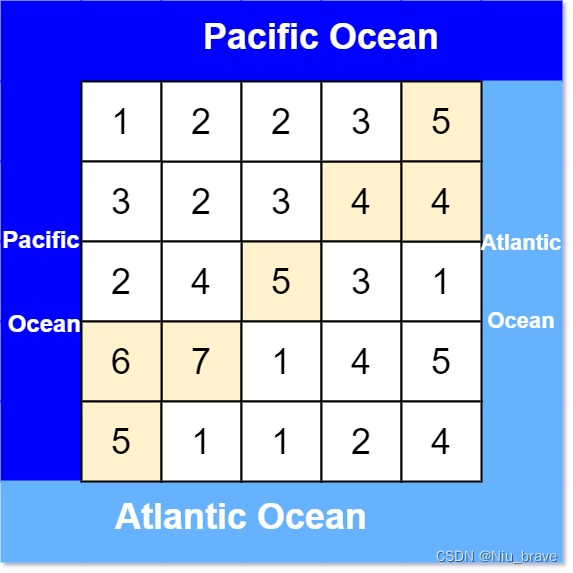
如图所示:
既能流向太平洋又能流向大西洋的格子便是被改为浅黄色的格子。这些格子都有一些特点便是这些格子都能从自己的位置开始由高到低的流向两边的两个大洋。我们的任务便是要找到这些格子然后将这些格子的下标给记录下来返回便是了。
3.题目接口
class Solution {
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
}
};4.解题思路及代码
这道题的解题思路和前面的那道题的解题思路其实也差不多,也是一个逆向思维的解法。先要明确的是水往低处流,所以我们从边界出发,因为边界的格子是和海洋相接的所以比边界高的格子便可以由边界流向海洋。然后比这个格子高的格子便可以由这个格子经过边界的格子流向海洋,这是一个递进的关系。只要我们将能流向某个大洋的这些格子标记一下,当一个格子有两种标记时便是可以流向两个大洋的,这些格子便是我们要找的。写成代码如下:
class Solution { public: int m,n; int dx[4] = {0,0,1,-1},dy[4] = {1,-1,0,0}; vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) { m = heights.size(),n = heights[0].size(); vector<vector<bool>>pac(m,vector<bool>(n)); vector<vector<bool>>alt(m,vector<bool>(n)); //寻找比边界高的格子并标记 for(int i = 0;i<m;i++) dfs(heights,i,0,pac);//左列 for(int i = 0;i<m;i++) dfs(heights,i,n-1,alt);//右列 for(int j = 0;j<n;j++) dfs(heights,0,j,pac);//第一行 for(int j = 0;j<n;j++) dfs(heights,m-1,j,alt);//最后一行 //记录结果 vector<vector<int>>ret; for(int i = 0;i<m;i++) { for(int j = 0;j<n;j++) { if(pac[i][j]&&alt[i][j]) { ret.push_back({i,j}); } } } return ret; } void dfs(vector<vector<int>>&heights,int i,int j,vector<vector<bool>>&vis) { vis[i][j] = true; for(int k = 0;k<4;k++) { int x = i+dx[k],y = j+dy[k]; if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&heights[x][y]>=heights[i][j]) { dfs(heights,x,y,vis); } } } };