前言
卷积的公式一般被表示为下式:
对新手来说完全看不懂这是干什么,这个问题需要结合卷积的应用场景来说。
原理
卷积比较广泛的应用是在信号与系统中,所以有些公式的定义会按照信息流的习惯。假设存在一串信号g(x)经过一个响应h(x)时他的响应会累加起来进行输出。其中:
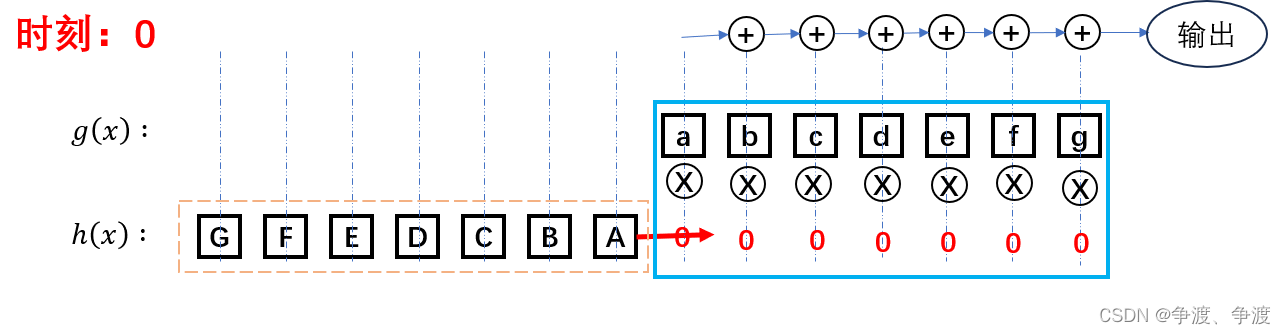
使用信息流的形式体现可以表示为下图:在时刻0时(第1个输出),信号和h(x)还没有进入响应函数g(x)模块中,因此输出结果为:(上下相遇时两信号相乘,输出时将个信号相加)
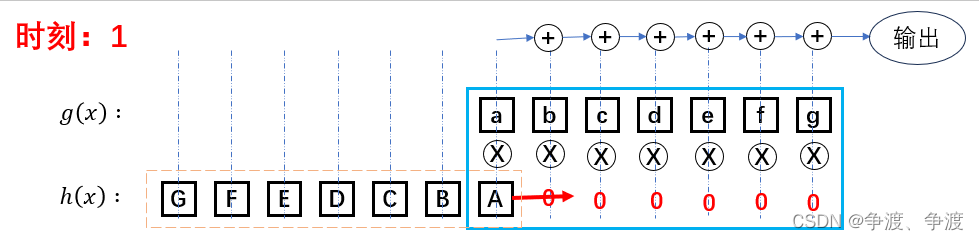
在时刻等于1(第2组)时,信号A与a出现交集,因此此时输出结果为:
(以下省略信号与0相乘的部分)
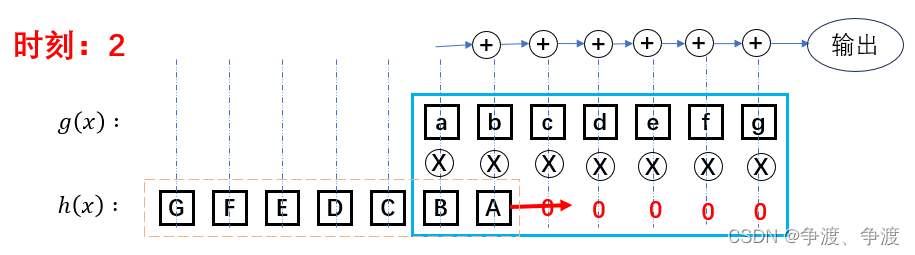
在时刻等于2(第3组)时,信号A与a出现交集,因此此时输出结果为:
以此类推在时刻等于7(第8组)时:
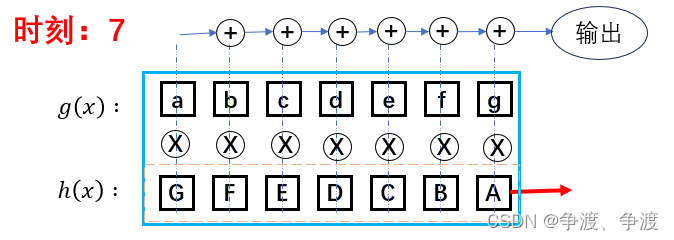
这个时候再来观察这个函数该怎么表示,g(x)在时间上是正常的顺序a b c d e f g,但是对于h(x),首先起作用的是A,也就是说生成信号的顺序应该是A B C D E F G,所以将两个函数表示为以下公式:
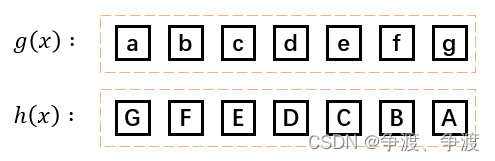
但是这个系统的输出怎么用函数表示呢?首先需要引入时间 t 的概念,因为不同时刻的结果不同,系统最终输出的结果是和时间相关的。这时只关注时刻7(第8组)的情况。输出的结果表示为函数其实是:
又可以写作下式:
用求和符号表示为:
写成连续函数即:
可以看出对信号有个时间上的倒序,这是因为在产生信号时坐标轴上最右侧的被我理解为是最后出现的,而在信号与系统中却是最早出现的。为了与传统数学作统一,做了这种调整。
个人的理解
应该就是因为有个时间倒序的问题才会把这种积分叫做卷积吧,不然就可以叫做正常的积分了,没必要重新定义一个概念。