3.3 逻辑斯蒂回归

目标：用判别模型解决分类问题

• 逻辑回归输出的是实例属于每个类别的似然概率，似然概率最大的类别就是分类结果
• 在一定条件下，逻辑回归模型与朴素贝叶斯分类器等价
• 多分类问题可以通过多次二分类或者Softmax回归解决

3.3.1 逻辑回归介绍

逻辑回归源于对线性回归算法的改进

通过引入单调可微函数 $g(\cdot )$ ，线性回归模型可以推广为 $y=g^{-1}(w^{T}x)$ ，进而将线性回归模型预测值与分类任务的离散标记联系起来。当 $g(\cdot )$ 取成对数形式时，线性回归就演变成了逻辑回归

对数几率函数

在简单的 二分类问题 中，分类的标记可以抽象为 $0$ 和 $1$ ，因而线性回归中的实值输出需要映射为二进制的结果

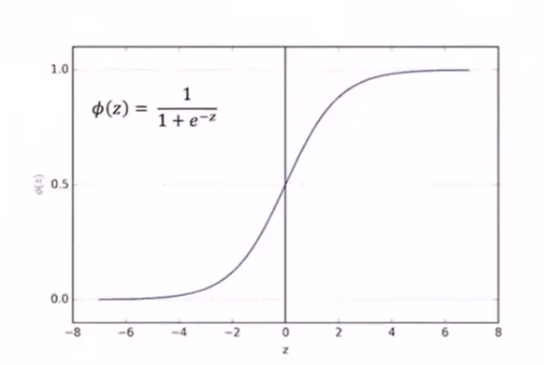
sigmod函数

逻辑回归中，实现这一映射的是对数几率函数，也即 sigmod函数
$$\varphi (z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-w^{T}x}}$$

• 对数几率函数能够将线性回归从负无穷到正无穷的输出范围压缩到 $(0,1)$ 之间

• 当线性回归结果是 $z=0$ 时，逻辑回归的结果是 $\varphi (z)=0.5$ ，这可以是做一个分界点

  当 $z>0$ ，则 $\varphi (z)>0.5$ ，此时逻辑回归的结果就被判为正例

  当 $z<0$ ，则 $\varphi (z)<0.5$ ，此时逻辑回归的结果就被判为负例

几率

如果将对数几率函数的结果 $\varphi (z)$ 视为样本 $x$ 作为正例的可能性 $P(y=1|x)$，则 $1-\varphi (z)$ 就是其作为反例的可能性 $P(y=0|x)$ ，两者比值 $0<\frac{\varphi (z)}{1-\varphi (z)}<\infty$ ，称为 几率 。

• $=1$，则说明概率相等
• $>1$ ，则说明 $\varphi (z)$ 的概率大，分为1类
• $<1$ ，则说明 $1-\varphi (z)$ 的概率大，为0类

对 几率 取对数，可得到
$$ln\frac{\varphi (z)}{1-\varphi (z)}=w^{T}x$$

• 线性回归的结果以对数几率的形式出现的

3.3.2 逻辑回归模型

输入： x = { x ( 1 ) , x ( 2 ) , ⋯   , x ( m ) } ∈ X ⊆ R m x=\{x^{(1)},x^{(2)},\cdots,x^{(m)}\}\in \mathcal{X}\subseteq R^m x={x(1),x(2),⋯,x(m)}∈X⊆Rm ；

• 需对输入的特征向量进行归一化

  若特征数值过大，样本会落在 sigmod 的饱和区，无法对 $x$ 进行正确分类

输出： Y ∈ { 0 , 1 } Y\in \{0,1\} Y∈{0,1}

逻辑回归模型为 条件概率表示的判别模型

$$\begin{gathered} \varphi (z)=P(y=1|x)=\frac{1}{1+e^{-w^{T}x}}=\frac{e^{w^{T}x}}{1+e^{w^{T}x}} \\ 1-\varphi (z)=P(y=0|x)=\frac{e^{-w^{T}x}}{1+e^{-w^{T}x}}=\frac{1}{1+e^{w^{T}x}} \end{gathered}$$

• ω = { ω ( 0 ) , ω ( 1 ) , ω ( 2 ) , ⋯   , ω ( m ) } ∈ R m + 1 \omega=\{\omega^{(0)},\omega^{(1)},\omega^{(2)},\cdots,\omega^{(m)}\}\in R^{m+1} ω={ω(0),ω(1),ω(2),⋯,ω(m)}∈Rm+1

对于给定的实例，逻辑回归模型比较两个条件概率值的大小，并将实例划分到概率较大的分类中

3.3.3 参数求解

假设样本独立同分布

学习时，逻辑回归模型在给定的训练数据集上应用 最大似然估计法 确定模型的参数

• 对于给定的数据 $(x_i,y_i)$ ，逻辑回归 使每个样本属于其真实标记的概率最大化，以此为依据确定 $w$ 的最优值

似然函数可表示为
$$L(w|x)=P(\omega |x)\stackrel{x_i独立同分布}{=}\prod _{i=1}^n[P(y=1|x_i,w){]}^{y_i}[1-P(y=1|x_i,w){]}^{1-y_i}$$

取对数后简化运算
ln ⁡ L ( w ∣ X ) = ∑ i = 1 n { y i ln ⁡ P ( Y = 1 ∣ x i , w ) + ( 1 − y i ) ln ⁡ [ 1 − P ( Y = 1 ∣ x i , w ) ] } \ln L(w\vert X)=\sum\limits_{i=1}^n\left\{y_i\ln P(Y=1\vert x_i,w)+(1-y_i)\ln \left[1-P(Y=1\vert x_i,w)\right]\right\} lnL(w∣X)=i=1∑n​{yi​lnP(Y=1∣xi​,w)+(1−yi​)ln[1−P(Y=1∣xi​,w)]}
由于单个样本的标记 $y_i$ 只能取得0或1，因而上式中的两项中只有一个非零值，代入对数几率，经过化简后可以得到
$$\ln L(w|X)=\sum _{i=1}^n\left[y_i(w^T{x}_i)-\ln (1+e^{w^T{x}_i})\right]$$
寻找上述函数的最大值就是以对数似然函数为目标函数的最优化问题，通常使用 梯度下降法 或 牛顿法 求解

逻辑斯蒂回归策略

后验概率最大化原则 $⟺$ 期望风险最小化策略
$$arg\underset{\omega }{\max }L(\omega )=arg\underset{\omega }{\max }\sum _{i=1}^n\left[y_i(w^T{x}_i)-\ln (1+e^{w^T{x}_i})\right]$$
基于 $\hat{\omega }$ 得到概率判别模型
$$\{\begin{array}{l}P(y=1|x)=\frac{e^{{\hat{\omega }}^T\cdot x}}{1+e^{{\hat{\omega }}^T\cdot x}}\\ P(y=0|x)=\frac{1}{1+e^{{\hat{\omega }}^T\cdot x}}\end{array}$$
通过梯度下降法/拟牛顿法 $\Rightarrow$ 数值解
$$\omega \leftarrow \omega -\eta \frac{\partial L(\omega )}{\partial \omega }$$

3.3.4 损失函数

线性模型的损失函数
$$J(\omega )=\frac{1}{2n}\sum _{i=-1}^n{\left[y_{\omega }(x_i)-y_i\right]}^2$$
逻辑斯蒂回归给出的是某一类概率
$$P(y=1|x,\omega )=\frac{1}{1+e^{-{\omega }^{T}x}}$$

预测 $y=1$ 且期望为 $1$ ，对于损失函数的估计有极大似然估计
$$\begin{array}{rl}J(\omega )& =-\frac{1}{n}\left[\sum _{i=1}^n\sum _{k=1}^{2}I(y_i=k)\ln P(y_i=k|x_i,\omega )\right]\\ & =-\frac{1}{n}\left[\sum _{i=1}^n{y}_i\ln P(y_i=1|x_i,\omega )+(1-y_i)\ln P(y_i=0|x_i,\omega )\right]\end{array}$$
$I\ln P$ 表示预测正确的部分，对于预测结果来说，越大越好；对于损失函数来说，越小越好，所以添加负号

对于损失函数的最优化，可通过梯度下降法
$${\omega }^{[t]}\leftarrow {\omega }^{[t+1]}-\alpha \frac{\partial J(\omega )}{\partial \omega }$$

3.3.5 应用：语句情感判断

将一句话映射为向量形式，对每句话进行逻辑斯蒂回归
$$\{\begin{array}{l}{x}_i:某个词词频\\ {\omega }_i:每个词权重\{\begin{array}{l}正面词{\omega }_i>0\\ 中性词{\omega }_i=0\\ 负面词{\omega }_i<0\end{array}\end{array}$$
整句话表示为
$$h=f(\sum _{i=1}^n{\omega }_i{x}_i)=f({\omega }^T\cdot x)$$
权重的计算
$$\{\begin{array}{l}某个词重要性：在本篇大量出现，在其他文章出现较少\\ termfrequency：文档中词频，越大表示越重要\\ InverseDocumentfrequency：其他语料库中出现的词频，越小表示其他文档中出现少，当前文档中的词比较重要\end{array}$$

3.3.6 多角度分析逻辑回归

信息论角度

当训练数据集是从所有数据中均匀抽取且数据量较大时，可以 从信息论角度 解释：

对数似然函数的最大化可以等效为待求模型与最大熵模型之间的KL散度的最小化。即逻辑回归对参数做出的额外假设是最少的。

数学角度

从 数学角度 看，线性回归与逻辑回归之间的关系在于非线性的对数似然函数

• 从特征空间看，两者的区别在于数据判断边界上的变化

  利用回归模型只能得到线性的判定边界；

  逻辑回归则在线性回归的基础上，通过对数似然函数的引入使判定边界的形状不再受限于直线

与朴素贝叶斯对比

联系

逻辑回归与朴素贝叶斯都是利用条件概率 $P(Y|X)$ 完成分类任务，二者在特定条件下可以等效

• 用朴素贝叶斯处理二分类任务时，假设对每个属性 $x_i$ ，属性条件概率 $P(X=x_i|Y=y_k)$ 都满足正态分布，且正态分布的标准差与输出标记 $Y$ 无关，则根据贝叶斯定理，后验概率可写成
  $$\begin{gathered} P(Y=0|X)=\frac{P(Y=0)\cdot P(X|Y=0)}{P(Y=1)\cdot P(X|Y=1)+P(Y=0)\cdot P(X|Y=0)} \\ =\frac{1}{1+e^{ln\frac{P(Y=1)\cdot P(X|Y=1)}{P(Y=0)\cdot P(X|Y=0)}}} \end{gathered}$$
  在条件独立性假设的前提下，类条件概率可以表示为属性条件概率的乘积。令先验概率 $P(Y=0)=p_0$ 并将满足正态分布的属性条件概率 $P(X^{(i)}|Y=y_k)$ 代入，可得
  $$P(Y=0|X)=\frac{1}{1+e^{ln\frac{1-p_0}{p_0}+\sum _i\left(\frac{{\mu }_{i1}-{\mu }_{i0}}{{\sigma }^2}{X}_i+\frac{{\mu }_{i0}^2-{\mu }_{i1}^2}{2{\sigma }_i^2}\right)}}$$
  可见，上式的形式和逻辑回归中条件概率 $P(Y=0|X)$ 是完全一致的，朴素贝叶斯学习器和逻辑回归模型学习到的是同一个模型

区别

属于不同的监督学习类型

• 朴素贝叶斯是生成模型的代表：先由训练数据估计出输入和输出的联合概率分布，再根据联合概率分布来生成符合条件的输出，$P(Y|X)$ 以后验概率的形式出现
• 逻辑回归是判别模型的代表：先由训练数据集估计出输入和输出的条件概率分布，再根据条件概率分布判定对于给定的输入应该选择哪种输出，$P(Y|X)$ 以似然概率的形式出现

当朴素贝叶斯学习器的条件独立性假设不成立时，逻辑回归与朴素贝叶斯方法通常会学习到不同的结果

• 当训练样本数接近无穷大时，逻辑回归的渐进分类准确率要优于朴素贝叶斯方法

  逻辑回归不依赖于条件独立性假设，偏差更小，但方差更大

• 当训练样本稀疏时，朴素贝叶斯的性能优于逻辑回归

收敛速度不同：逻辑回归的收敛速度慢于朴素贝叶斯方法

3.3.7 从二分类到多分类问题

要让逻辑回归处理多分类问题，需要做一些改进

多次二分类

通过多次二分类实现多个类别的标记

• 等效为直接将逻辑回归应用在每个类别上，对每个类别建立一个二分类器

  如果输出的类别标记数为 $m$ ，就可以得到 $m$ 个针对不同标记的二分类逻辑回归模型，对一个实例的分类结果就是这 $m$ 个分类函数中输出值最大的那个

• 对一个实例执行分类需要多次使用逻辑回归算法，效率低下

softmax

直接修改逻辑回归的似然概率，使之适应多分类问题——softmax回归

softmax给出的是实例在每一种分类结果下出现的概率

y = { 1 , 2 , ⋯   , K } y=\{1,2,\cdots,K\} y={1,2,⋯,K}
$$\begin{array}{rl}P(y=k|x)& =\frac{e^{w_k^{T}x}}{1+\sum _{k=1}^{K-1}{e}^{w_k^{T}x}},k=1,2,\cdots ,K-1\\ P(y=K|x)& =\frac{1}{1+\sum _{k=1}^{K-1}{e}^{w_k^{T}x}}\\ P(y=K|x)& =1-P(y=k|x)=1-\frac{\sum _{k=1}^{K-1}{e}^{w_k^{T}x}}{1+\sum _{k=1}^{K-1}{e}^{w_k^{T}x}}\end{array}$$

• $w_k$ 表示和类别 $k$ 相关的权重参数

Softmax回归模型的训练与逻辑回归模型类似，都可以转化为通过梯度下降法或者拟牛顿法解决最优化问题

两种方式对比

输出结果只能是属于一个类别时，Softmax分类器更加高效

输出结果可能出现交叉情况时，多个二分类逻辑回归模型性能好，可以得到多个类别的标记