二次曲面
文章目录
- 二次曲面
- 知识点1 二次曲面的概念
- 知识点2 常见的二次曲面
- 知识点3 空间曲面小结
知识点1 二次曲面的概念
定义1 三元二次方程(二次项系数不全为0)
A x 2 + B y 2 + C z 2 + D x y + E y z + F z x + G x + H y + I z + J = 0 Ax^2+By^2+Cz^2+Dxy+Eyz+Fzx+Gx+Hy+Iz+J=0 Ax2+By2+Cz2+Dxy+Eyz+Fzx+Gx+Hy+Iz+J=0
所表示的空间曲面称为二次曲面。
2.常见二次曲面
椭球面、抛物面、双曲面
研究二次曲面特性的基本方法:截痕法
知识点2 常见的二次曲面
(1)椭球面
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 a2x2+b2y2+c2z2=1 (a,b,c为正数)
①范围: ∣ x ∣ ≤ a , ∣ y ∣ ≤ b , ∣ z ∣ ≤ c |x|\leq a, |y|\leq b,|z|\leq c ∣x∣≤a,∣y∣≤b,∣z∣≤c
②与坐标面的交线:椭圆
{
x
2
a
2
+
y
2
b
2
=
1
z
=
0
{
y
2
b
2
+
z
2
c
2
=
1
x
=
0
{
x
2
a
2
+
z
2
c
2
=
1
y
=
0
\begin{cases} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ z=0 \end{cases} \begin{cases} \frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \\ x=0 \end{cases} \begin{cases} \frac{x^2}{a^2}+\frac{z^2}{c^2}=1 \\ y=0 \end{cases}
{a2x2+b2y2=1z=0{b2y2+c2z2=1x=0{a2x2+c2z2=1y=0
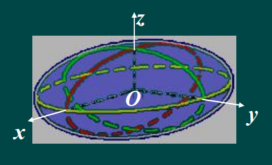
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 a2x2+b2y2+c2z2=1 (a,b,c为正数)
③截痕:与
z
=
z
1
(
∣
z
1
∣
<
c
)
z=z_1 (|z_1|<c)
z=z1(∣z1∣<c)的交线为椭圆:
{
x
2
a
2
c
2
(
c
2
−
z
1
2
)
+
y
2
b
2
c
2
(
c
2
−
z
1
2
)
=
1
z
=
z
1
\begin{cases} \frac{x^2}{\frac{a^2}{c^2}(c^2-z_1^2)}+\frac{y^2}{\frac{b^2}{c^2}(c^2-z_1^2)}=1 \\ z=z_1 \end{cases}
⎩
⎨
⎧c2a2(c2−z12)x2+c2b2(c2−z12)y2=1z=z1
同样
y
=
y
1
(
∣
y
1
∣
≤
b
)
y=y_1(|y_1|\leq b)
y=y1(∣y1∣≤b)及
x
=
x
1
(
∣
x
1
∣
≤
a
)
x=x_1 (|x_1|\leq a)
x=x1(∣x1∣≤a)的截痕也为椭圆。
④当a=b=c时为球面。
(2)抛物面
①椭圆抛物面
x 2 2 p + y 2 z q = z \frac{x^2}{2p}+\frac{y^2}{zq}=z 2px2+zqy2=z (p,q同号)
特别,当 p =q 时为绕 z 轴的旋转抛物面。
②双曲抛物面(鞍形曲面)
− x 2 z p + y 2 z q = z -\frac{x^2}{zp}+\frac{y^2}{zq}=z −zpx2+zqy2=z

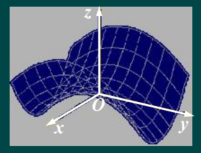
(3)双曲面
①单叶双曲面
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 a2x2+b2y2+c2z2=1 (a,b,c为正数)
平面 z = z 1 z=z_1 z=z1上的截痕为椭圆。
②双叶双曲面
x 2 a 2 + y 2 b 2 − z 2 c 2 = − 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1 a2x2+b2y2−c2z2=−1
平面 y = y 1 y=y_1 y=y1上的截痕为双曲线
平面 x = x 1 x=x_1 x=x1上的截痕为双曲线
平面 z = z 1 ( ∣ z 1 ∣ > c ) z=z_1(|z_1|>c) z=z1(∣z1∣>c)上的截痕为椭圆
知识点3 空间曲面小结
1.空间曲面 --> 三元方程 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0.
• 球面 ( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R 2 (x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2 (x−x0)2+(y−y0)2+(z−z0)2=R2
• 旋转曲面
如,曲线 { f ( y , z ) = 0 x = 0 \begin{cases} f(y,z)=0 \\ x=0 \end{cases} {f(y,z)=0x=0 绕 z 轴的旋转曲面: f ( ± x 2 + y 2 , z ) = 0 f(\pm \sqrt{x^2+y^2,z})=0 f(±x2+y2,z)=0
• 柱面
如,曲面 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0 表示母线平行 z 轴的柱面。又如,椭圆柱面,双曲柱面,抛物柱面等。
2.二次曲面—> 三元二次方程
• 椭球面:椭圆抛物面 双曲抛物面
( p,q同号) x 2 2 p + y 2 2 q = z , − x 2 2 p + y 2 2 q = z \frac{x^2}{2p}+\frac{y^2}{2q}=z , -\frac{x^2}{2p}+\frac{y^2}{2q}=z 2px2+2qy2=z,−2px2+2qy2=z
• 双曲面:单叶双曲面 双叶双曲面
x 2 a 2 + y 2 b 2 , x 2 a 2 + y 2 b 2 − z 2 c 2 = − 1 \frac{x^2}{a^2}+\frac{y^2}{b^2} , \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1 a2x2+b2y2,a2x2+b2y2−c2z2=−1
$
• 双曲面:单叶双曲面 双叶双曲面
x 2 a 2 + y 2 b 2 , x 2 a 2 + y 2 b 2 − z 2 c 2 = − 1 \frac{x^2}{a^2}+\frac{y^2}{b^2} , \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1 a2x2+b2y2,a2x2+b2y2−c2z2=−1
一次曲面:平面 三元一次方程