循环神经网络

学习视频：循环神经网络 RNN【动手学深度学习v2】

官方笔记：循环神经网络

1.算法介绍

潜变量自回归模型

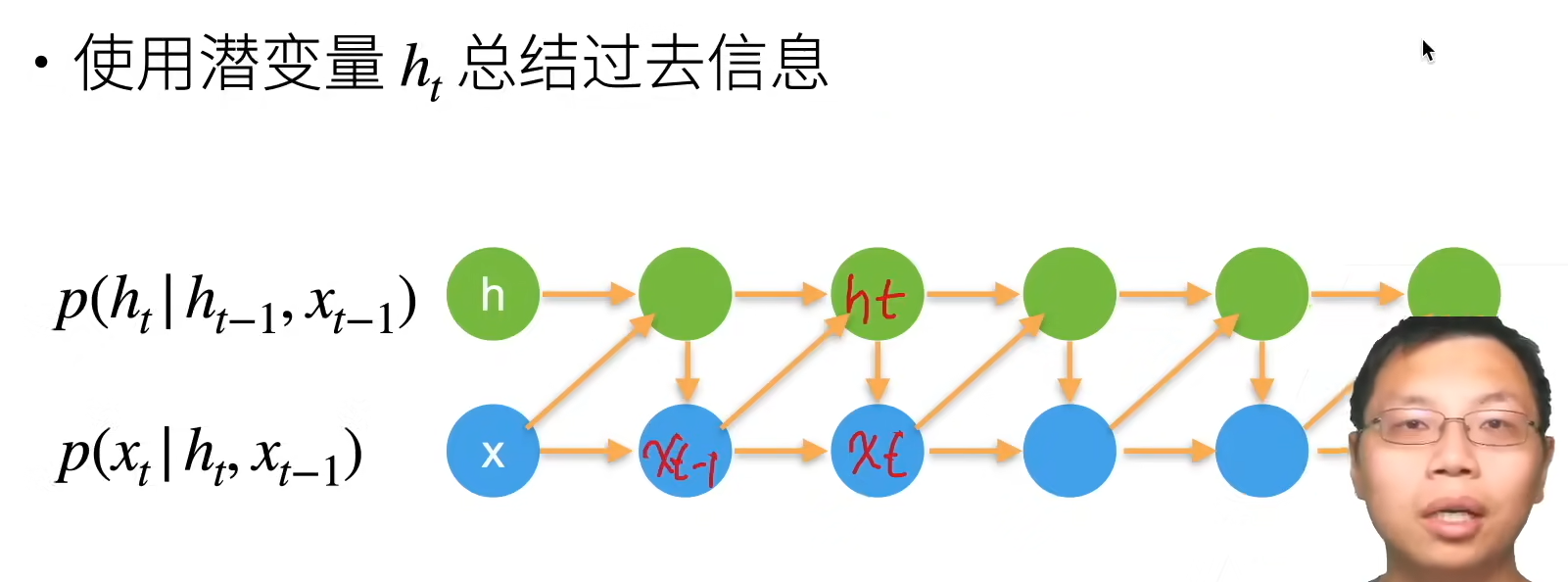
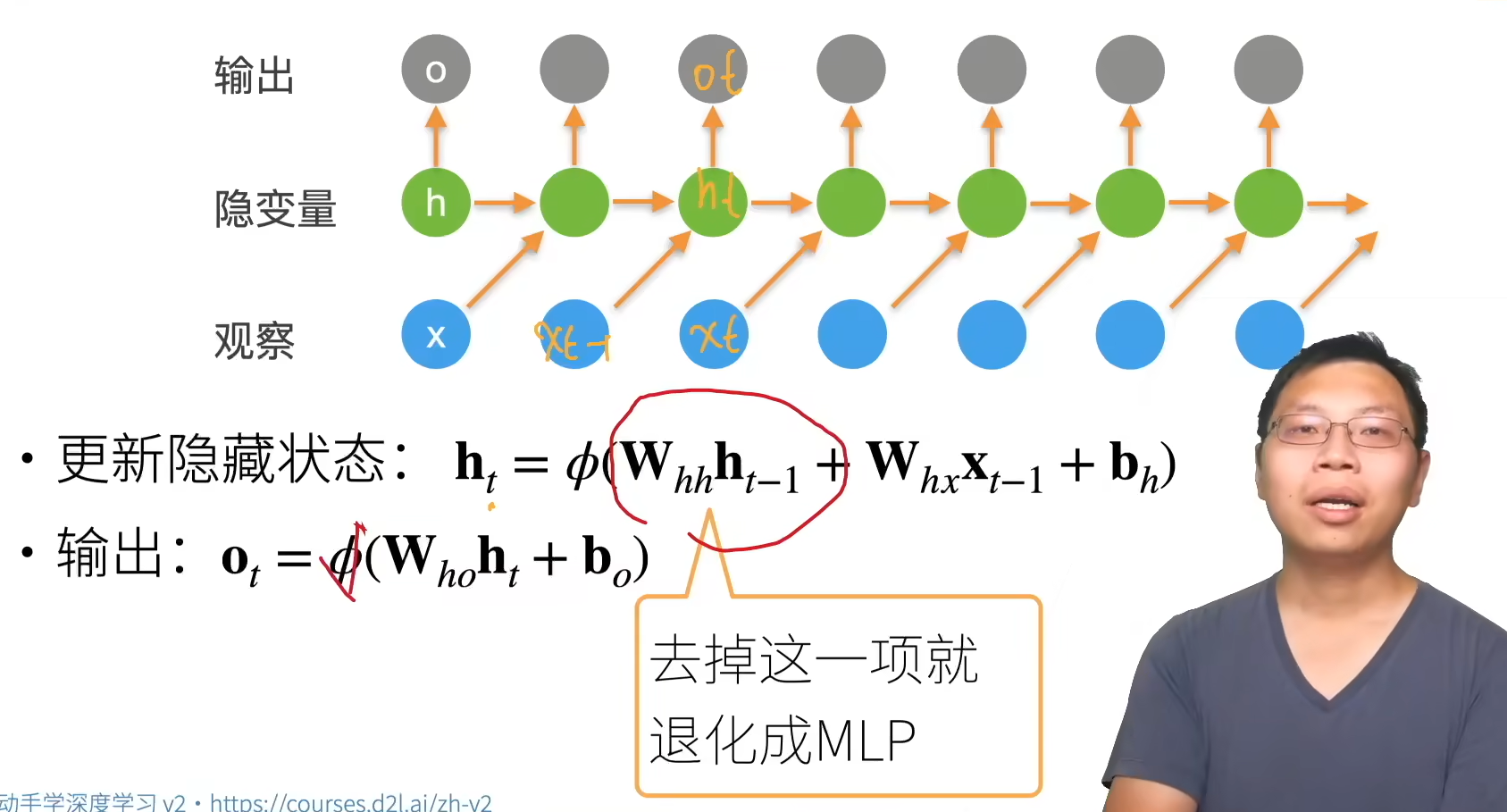
1.1无隐状态的神经网络(多层感知机)

1.2有隐状态的循环神经网络

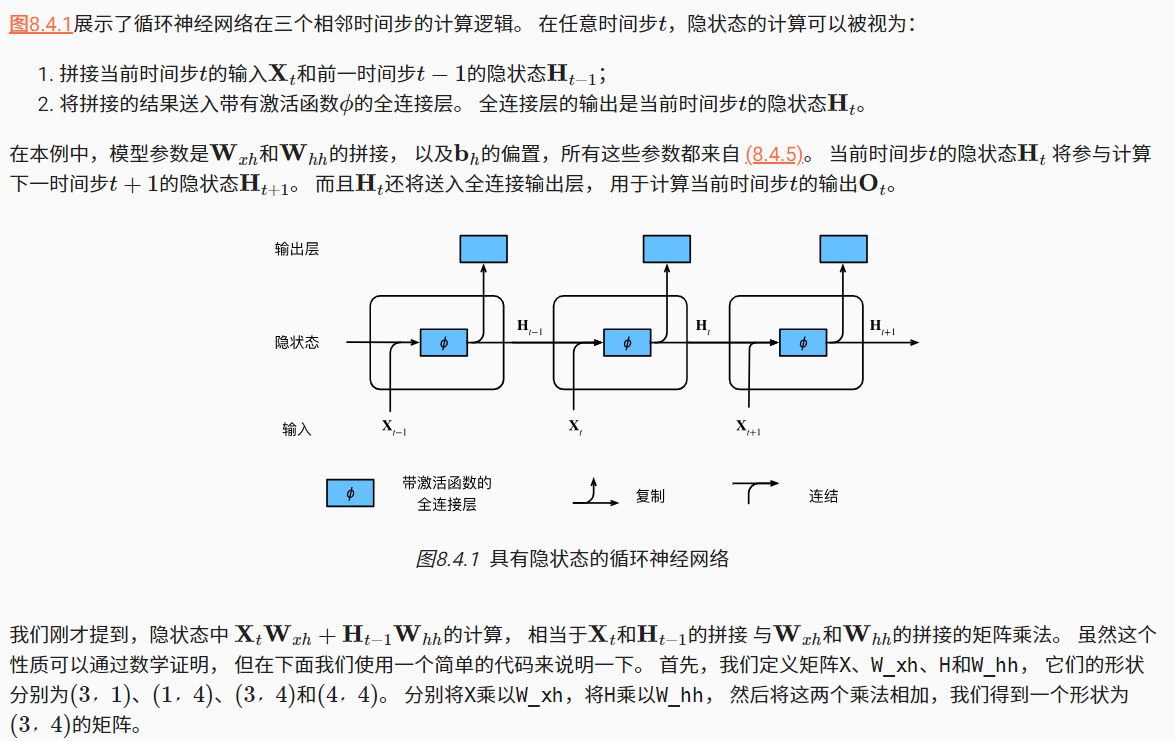
循环神经网络

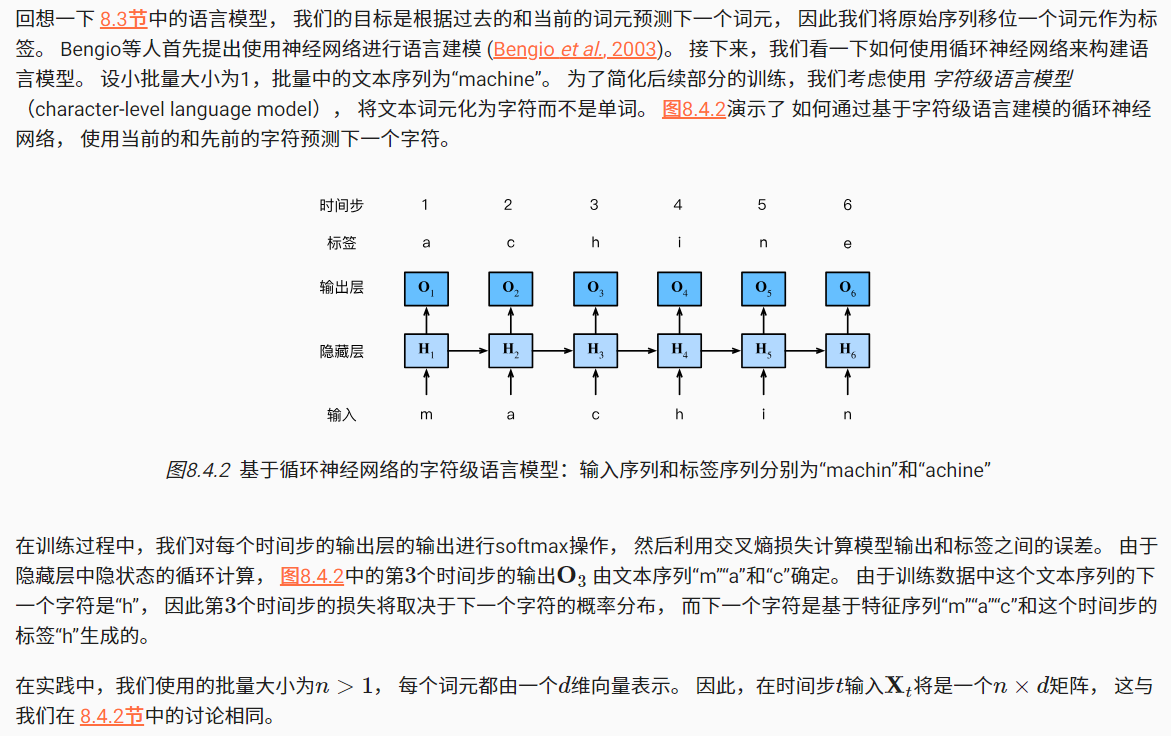
1.3基于循环神经网络的字符级语言模型

1.4困惑度

• 在最好的情况下，模型总是完美地估计标签词元的概率为1，在这种情况下，模型的困惑度为1
• 在最坏的情况下，模型总是预测标签词元的概率为0。在这种情况下，困惑度是正无穷大
• 在基线上，该模型的预测是词表的所有可用词元上的均匀分布。 在这种情况下，困惑度等于词表中唯一词元的数量。 事实上，如果我们在没有任何压缩的情况下存储序列， 这将是我们能做的最好的编码方式。 因此，这种方式提供了一个重要的上限， 而任何实际模型都必须超越这个上限。

梯度裁剪

总结：

• 循环神经网络的输出取决于当下输入和前一时间的隐变量
• 应用到语言模型中，循环神经网络根据当前词预测下一次时刻词
• 通常使用困惑度来衡量语言模型的好坏

2.RNN从零开始实现

学习视频：循环神经网络 RNN 的实现【动手学深度学习v2】

官方笔记：

循环神经网络的从零开始实现

循环神经网络的简洁实现

2.1读取数据集

%matplotlib inline
import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

2.2独热编码

F.one_hot(torch.tensor([0, 2]), len(vocab))

'''
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0],
        [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
         0, 0, 0, 0]])
'''

我们每次采样的小批量数据形状是二维张量： （批量大小，时间步数）。 one_hot函数将这样一个小批量数据转换成三维张量， 张量的最后一个维度等于词表大小（len(vocab)）。 我们经常转换输入的维度，以便获得形状为 （时间步数，批量大小，词表大小）的输出。 这将使我们能够更方便地通过最外层的维度， 一步一步地更新小批量数据的隐状态。

X = torch.arange(10).reshape((2, 5))
F.one_hot(X.T, 28).shape

'''
torch.Size([5, 2, 28])
'''

2.3初始化模型参数

接下来，我们初始化循环神经网络模型的模型参数。 隐藏单元数num_hiddens是一个可调的超参数。 当训练语言模型时，输入和输出来自相同的词表。 因此，它们具有相同的维度，即词表的大小。

def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.01

    # 隐藏层参数
    W_xh = normal((num_inputs, num_hiddens))
    W_hh = normal((num_hiddens, num_hiddens))
    b_h = torch.zeros(num_hiddens, device=device)
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

2.4循环神经网络模型

为了定义循环神经网络模型， 我们首先需要一个init_rnn_state函数在初始化时返回隐状态。 这个函数的返回是一个张量，张量全用0填充， 形状为（批量大小，隐藏单元数）。 在后面的章节中我们将会遇到隐状态包含多个变量的情况， 而使用元组可以更容易地处理些。

def init_rnn_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

下面的rnn函数定义了如何在一个时间步内计算隐状态和输出。 循环神经网络模型通过inputs最外层的维度实现循环， 以便逐时间步更新小批量数据的隐状态H。 此外，这里使用tanh函数作为激活函数，当元素在实数上满足均匀分布时，tanh函数的平均值为0。

def rnn(inputs, state, params):
    # inputs的形状：(时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    # X的形状：(批量大小，词表大小)
    for X in inputs:
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

定义了所有需要的函数之后，接下来我们创建一个类来包装这些函数， 并存储从零开始实现的循环神经网络模型的参数。

class RNNModelScratch: #@save
    """从零开始实现的循环神经网络模型"""
    def __init__(self, vocab_size, num_hiddens, device,
                 get_params, init_state, forward_fn):
        self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
        self.params = get_params(vocab_size, num_hiddens, device)
        self.init_state, self.forward_fn = init_state, forward_fn

    def __call__(self, X, state):
        X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
        return self.forward_fn(X, state, self.params)

    def begin_state(self, batch_size, device):
        return self.init_state(batch_size, self.num_hiddens, device)

让我们检查输出是否具有正确的形状。 例如，隐状态的维数是否保持不变

num_hiddens = 512
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                      init_rnn_state, rnn)
state = net.begin_state(X.shape[0], d2l.try_gpu())
Y, new_state = net(X.to(d2l.try_gpu()), state)
Y.shape, len(new_state), new_state[0].shape

'''
(torch.Size([10, 28]), 1, torch.Size([2, 512]))
'''

我们可以看到输出形状是（时间步数×批量大小，词表大小）， 而隐状态形状保持不变，即（批量大小，隐藏单元数）。

2.5预测

让我们首先定义预测函数来生成prefix之后的新字符， 其中的prefix是一个用户提供的包含多个字符的字符串。 在循环遍历prefix中的开始字符时， 我们不断地将隐状态传递到下一个时间步，但是不生成任何输出。 这被称为预热（warm-up）期， 因为在此期间模型会自我更新（例如，更新隐状态）， 但不会进行预测。 预热期结束后，隐状态的值通常比刚开始的初始值更适合预测， 从而预测字符并输出它们。

def predict_ch8(prefix, num_preds, net, vocab, device):  #@save
    """在prefix后面生成新字符"""
    state = net.begin_state(batch_size=1, device=device)
    outputs = [vocab[prefix[0]]]
    get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
    for y in prefix[1:]:  # 预热期
        _, state = net(get_input(), state)
        outputs.append(vocab[y])
    for _ in range(num_preds):  # 预测num_preds步
        y, state = net(get_input(), state)
        outputs.append(int(y.argmax(dim=1).reshape(1)))
    return ''.join([vocab.idx_to_token[i] for i in outputs])

现在我们可以测试predict_ch8函数。 我们将前缀指定为time traveller， 并基于这个前缀生成10个后续字符。 鉴于我们还没有训练网络，它会生成荒谬的预测结果。

predict_ch8('time traveller ', 10, net, vocab, d2l.try_gpu())

'''
'time traveller aaaaaaaaaa'
'''

2.6梯度裁剪

def grad_clipping(net, theta):  #@save
    """裁剪梯度"""
    if isinstance(net, nn.Module):
        params = [p for p in net.parameters() if p.requires_grad]
    else:
        params = net.params
    norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
    if norm > theta:
        for param in params:
            param.grad[:] *= theta / norm

2.7训练

#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
    """训练网络一个迭代周期（定义见第8章）"""
    state, timer = None, d2l.Timer()
    metric = d2l.Accumulator(2)  # 训练损失之和,词元数量
    for X, Y in train_iter:
        if state is None or use_random_iter:
            # 在第一次迭代或使用随机抽样时初始化state
            state = net.begin_state(batch_size=X.shape[0], device=device)
        else:
            if isinstance(net, nn.Module) and not isinstance(state, tuple):
                # state对于nn.GRU是个张量
                state.detach_()
            else:
                # state对于nn.LSTM或对于我们从零开始实现的模型是个张量
                for s in state:
                    s.detach_()
        y = Y.T.reshape(-1)
        X, y = X.to(device), y.to(device)
        y_hat, state = net(X, state)
        l = loss(y_hat, y.long()).mean()
        if isinstance(updater, torch.optim.Optimizer):
            updater.zero_grad()
            l.backward()
            grad_clipping(net, 1)
            updater.step()
        else:
            l.backward()
            grad_clipping(net, 1)
            # 因为已经调用了mean函数
            updater(batch_size=1)
        metric.add(l * y.numel(), y.numel())
    return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()

循环神经网络模型的训练函数既支持从零开始实现， 也可以使用高级API来实现。

#@save
def train_ch8(net, train_iter, vocab, lr, num_epochs, device,
              use_random_iter=False):
    """训练模型（定义见第8章）"""
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
                            legend=['train'], xlim=[10, num_epochs])
    # 初始化
    if isinstance(net, nn.Module):
        updater = torch.optim.SGD(net.parameters(), lr)
    else:
        updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
    predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)
    # 训练和预测
    for epoch in range(num_epochs):
        ppl, speed = train_epoch_ch8(
            net, train_iter, loss, updater, device, use_random_iter)
        if (epoch + 1) % 10 == 0:
            print(predict('time traveller'))
            animator.add(epoch + 1, [ppl])
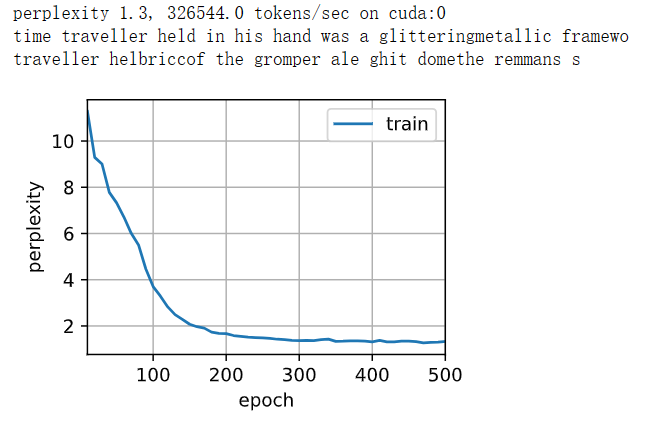
    print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
    print(predict('time traveller'))
    print(predict('traveller'))

现在，训练循环神经网络模型。 因为我们在数据集中只使用了10000个词元， 所以模型需要更多的迭代周期来更好地收敛。

num_epochs, lr = 500, 1
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu())

最后，检查一下使用随机抽样方法的结果。

net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                      init_rnn_state, rnn)
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(),
          use_random_iter=True)

3.RNN简洁实现

3.1读取数据集

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

3.2定义模型

高级API提供了循环神经网络的实现。 我们构造一个具有256个隐藏单元的单隐藏层的循环神经网络层rnn_layer。 事实上，我们还没有讨论多层循环神经网络的意义，现在仅需要将多层理解为一层循环神经网络的输出被用作下一层循环神经网络的输入就足够了。

num_hiddens = 256
rnn_layer = nn.RNN(len(vocab), num_hiddens)

我们使用张量来初始化隐状态，它的形状是（隐藏层数，批量大小，隐藏单元数）。

state = torch.zeros((1, batch_size, num_hiddens))
state.shape

'''
torch.Size([1, 32, 256])
'''

通过一个隐状态和一个输入，我们就可以用更新后的隐状态计算输出。 需要强调的是，rnn_layer的“输出”（Y）不涉及输出层的计算： 它是指每个时间步的隐状态，这些隐状态可以用作后续输出层的输入。

X = torch.rand(size=(num_steps, batch_size, len(vocab)))
Y, state_new = rnn_layer(X, state)
Y.shape, state_new.shape

我们为一个完整的循环神经网络模型定义了一个RNNModel类。 注意，rnn_layer只包含隐藏的循环层，我们还需要创建一个单独的输出层。

#@save
class RNNModel(nn.Module):
    """循环神经网络模型"""
    def __init__(self, rnn_layer, vocab_size, **kwargs):
        super(RNNModel, self).__init__(**kwargs)
        self.rnn = rnn_layer
        self.vocab_size = vocab_size
        self.num_hiddens = self.rnn.hidden_size
        # 如果RNN是双向的（之后将介绍），num_directions应该是2，否则应该是1
        if not self.rnn.bidirectional:
            self.num_directions = 1
            self.linear = nn.Linear(self.num_hiddens, self.vocab_size)
        else:
            self.num_directions = 2
            self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)

    def forward(self, inputs, state):
        X = F.one_hot(inputs.T.long(), self.vocab_size)
        X = X.to(torch.float32)
        Y, state = self.rnn(X, state)
        # 全连接层首先将Y的形状改为(时间步数*批量大小,隐藏单元数)
        # 它的输出形状是(时间步数*批量大小,词表大小)。
        output = self.linear(Y.reshape((-1, Y.shape[-1])))
        return output, state

    def begin_state(self, device, batch_size=1):
        if not isinstance(self.rnn, nn.LSTM):
            # nn.GRU以张量作为隐状态
            return  torch.zeros((self.num_directions * self.rnn.num_layers,
                                 batch_size, self.num_hiddens),
                                device=device)
        else:
            # nn.LSTM以元组作为隐状态
            return (torch.zeros((
                self.num_directions * self.rnn.num_layers,
                batch_size, self.num_hiddens), device=device),
                    torch.zeros((
                        self.num_directions * self.rnn.num_layers,
                        batch_size, self.num_hiddens), device=device))

3.3训练与预测

在训练模型之前，让我们基于一个具有随机权重的模型进行预测。

device = d2l.try_gpu()
net = RNNModel(rnn_layer, vocab_size=len(vocab))
net = net.to(device)
d2l.predict_ch8('time traveller', 10, net, vocab, device)

'''
'time travellerialcaaiala'
'''

很明显，这种模型根本不能输出好的结果，接下来，使用之前定义的超参数调用train_ch8，并且使用高级API训练模型

num_epochs, lr = 500, 1
d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device)