目录

题目：

示例：

分析：

代码：

---

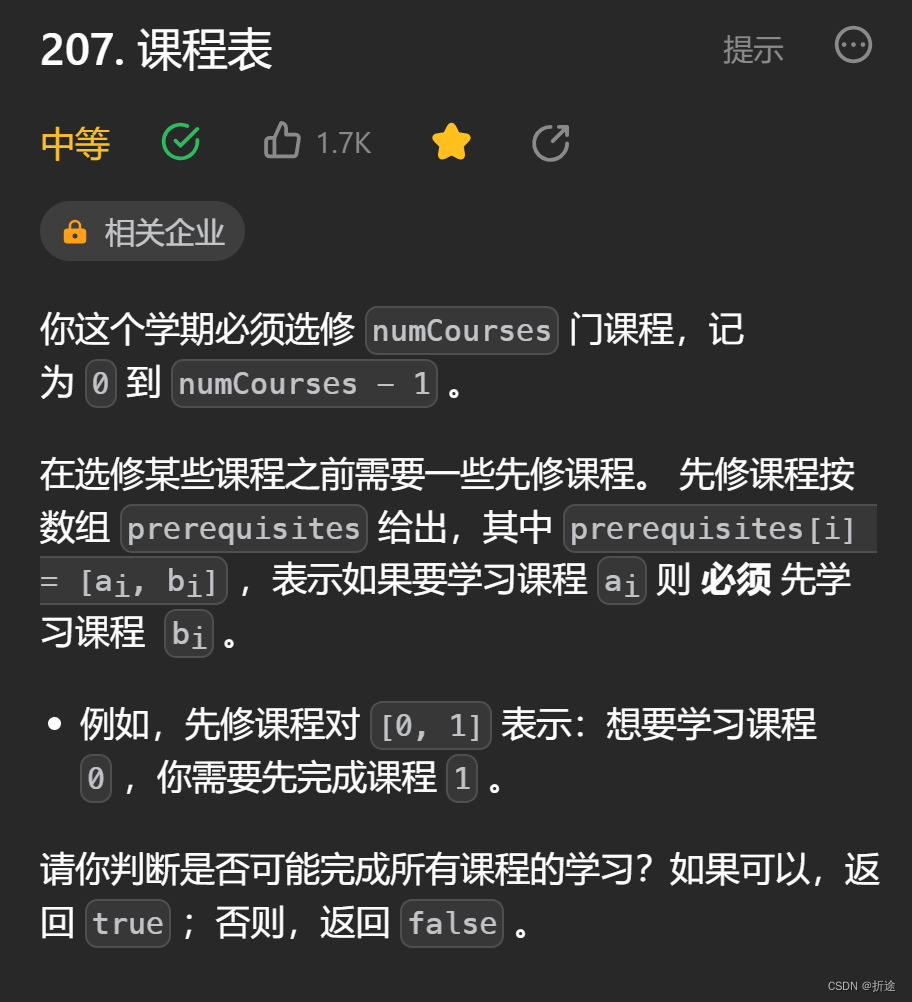
题目：

示例：

分析：

题目给我们一些课程的先修关系，也就是有些课我们需要先去学其他的课程才能学习，问我们是否可以学习完所有的课程。

这道题和LeetCode75系列的第四十三题钥匙和房间很类似，不过不一样的是本题中题目没有告诉我们一开始学习的课程是什么，也就是说我们可以先学习所有没有先修关系的课程，然后再看看能不能学完所有的课程。

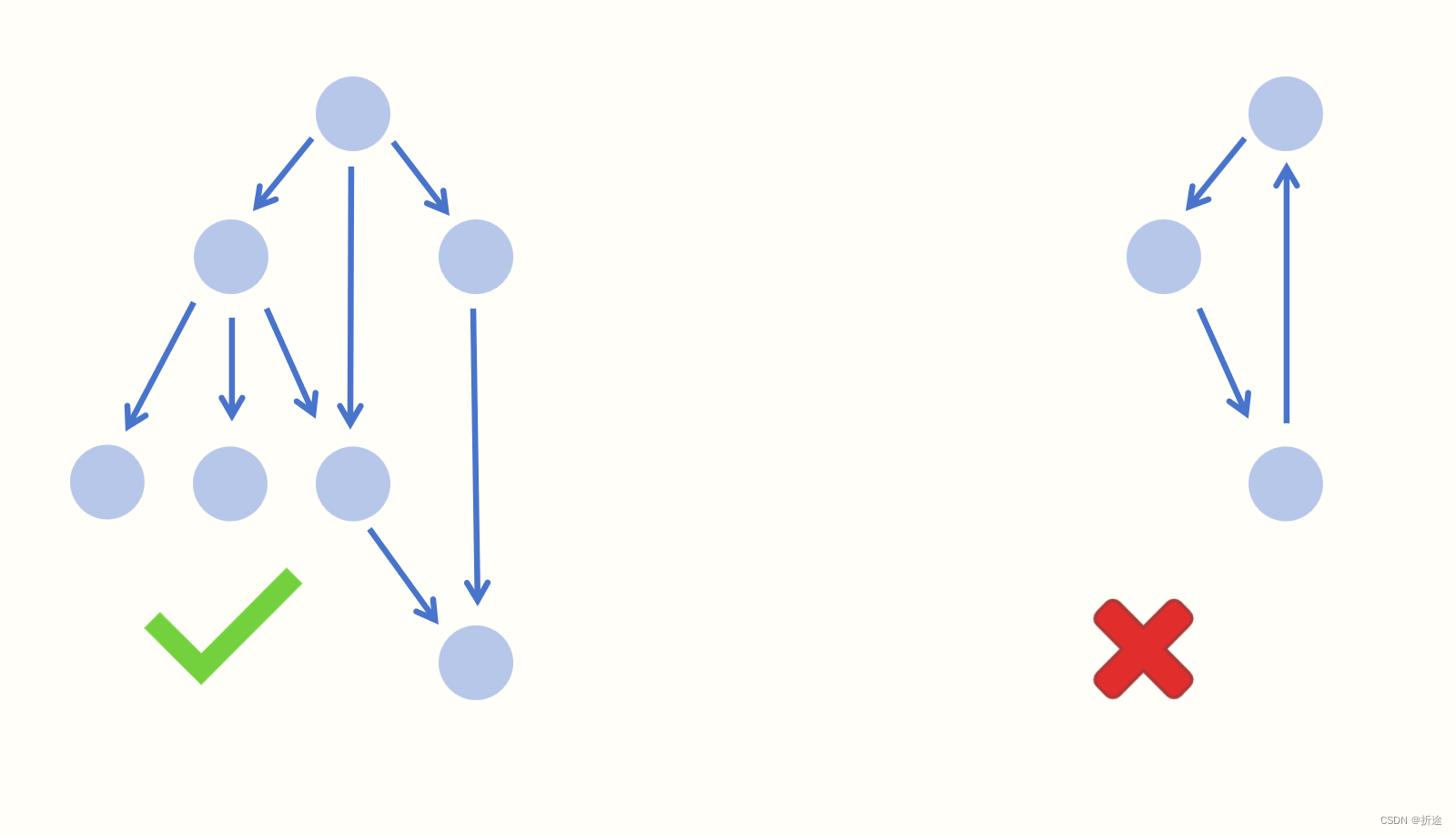
我们可以将课程的先修关系转变为有向图，然后我们就可以很清晰的发现，不能学完所有课程的情况只有一种，那就是有向图中有环。

我个人喜欢DFS，所以以下代码是DFS。

首先先用题目给出的先修关系构建出有向图，我这边用的是map，用邻接矩阵也是可以的。

构建完毕之后我们去遍历每个科目，再对每个科目用递归去寻找它们的先修科目以及先修科目的先修科目，如果找到了和自身一样的科目，那么就表示找到了图中的环，即我们不能学完所有科目。

在递归的时候我们需要传入当前递归的科目，以及初始的科目，还有一个已经遍历过的科目数组。如果当前的科目等于初始的科目，那么找到环。如果递归到了之前遍历过的科目，那么我们并不能说明找到了环，并且由于之前是递归过这个科目的，所以也要退出本次循环。

可能有小伙伴会有疑惑，如果我们递归到了之前遍历过的科目，那么不是说明我们又绕回去了，也是有环的吗？为什么说不能说明找到了环呢？

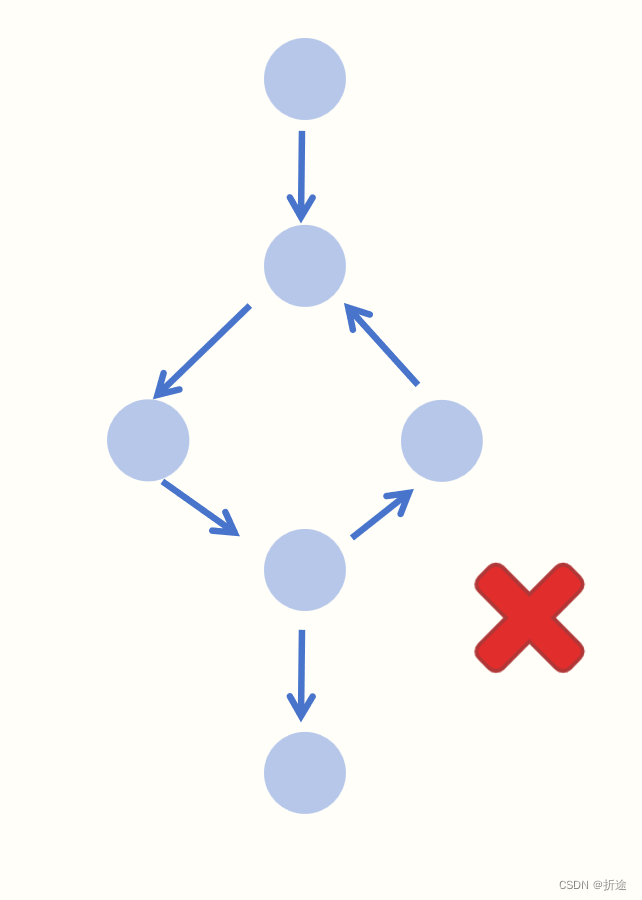
一般情况下是有环的，但是有个特殊情况，就是下面这样：

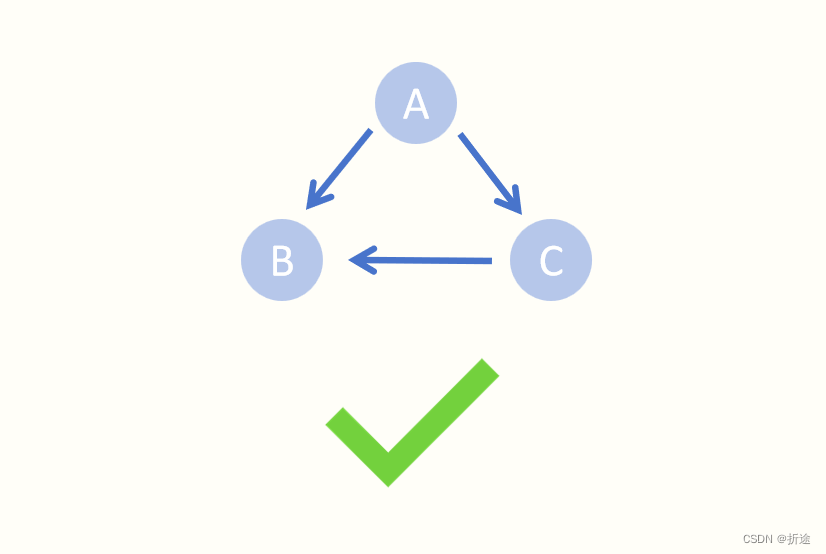
A的先修课程是B和C，而C的先修课程是B。我们可以先修B然后C最后A，最终是可以学完所有课程的，

但如果我们递归到之前递归过的课程就认定有环的话，会把这种无环的情况也归为有环，因此就算我们递归到了之前递归过的课程也不能断定有环。

代码：

lass Solution {
private:
    unordered_map<int,vector<int>>m;
public:
    bool find(int cur,int init,unordered_set<int>&s){
        if(cur==init) return false;     //如果先修课的先修课中含有最初始的课程,那么闭环.
        if(s.count(cur)) return true;   //如果递归到了之前递归过的课程,那么结束本次遍历,无法判断是否闭环
        s.insert(cur);                  //添加递归过的课程避免陷入死循环
        for(auto i:m[cur]){             //递归本次课程的先修课
            if(!find(i,init,s)) return false;
        }
        return true;
    }

    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        for(auto& p:prerequisites){     //构建有向图
            if(m.find(p[0])==m.end()) m[p[0]]=vector<int>(0);
            m[p[0]].push_back(p[1]);
        }
        for(int i=0;i<numCourses;i++){ 
            unordered_set<int>s;
            //寻找课程的先修课中是否包含自身
            for(auto j:m[i]){
                if(!find(j,i,s)) return false;
            }
        }
        return true;
    }
};