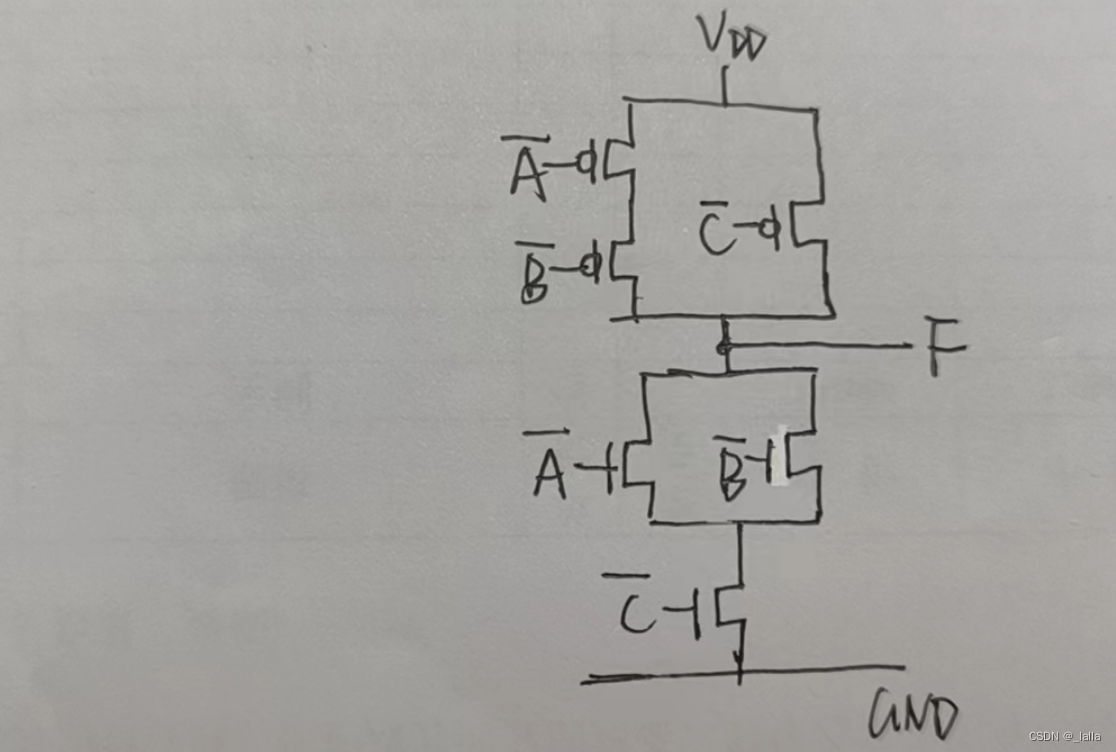
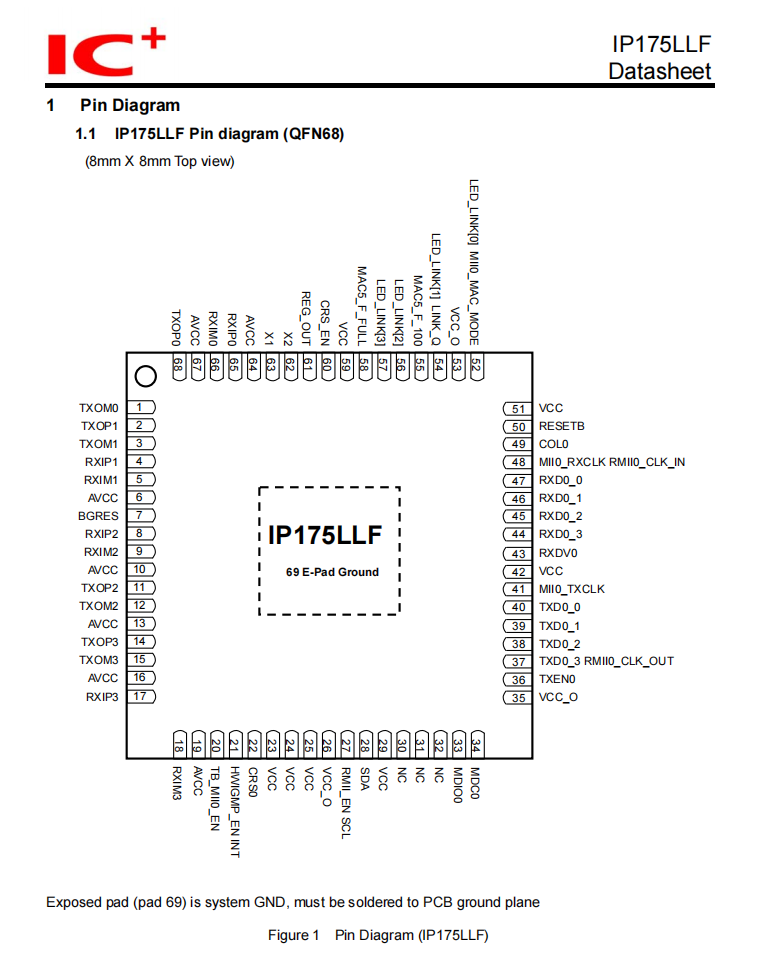
lap.lapjv貌似是一个比匈牙利算法快的算法。
函数的参数：
如果是非方阵，extend_cost需要是True。
cost_limit，小于等于这个数值的分配代价才会分配。

def lapjv(*args, **kwargs): # real signature unknown
    """
    Solve linear assignment problem using Jonker-Volgenant algorithm.
    
        Parameters
        ----------
        cost: (N,N) ndarray
            Cost matrix. Entry `cost[i, j]` is the cost of assigning row `i` to
            column `j`.
        extend_cost: bool, optional
            Whether or not extend a non-square matrix. Default: False.
        cost_limit: double, optional
            An upper limit for a cost of a single assignment. Default: `np.inf`.
        return_cost: bool, optional
            Whether or not to return the assignment cost.
    
        Returns
        -------
        opt: double
            Assignment cost. Not returned if `return_cost is False`.
        x: (N,) ndarray
            Assignment. `x[i]` specifies the column to which row `i` is assigned.
        y: (N,) ndarray
            Assignment. `y[j]` specifies the row to which column `j` is assigned.
    
        Notes
        -----
        For non-square matrices (with `extend_cost is True`) or `cost_limit` set
        low enough, there will be unmatched rows, columns in the solution `x`, `y`.
        All such entries are set to -1.
    """
    pass

一个例子：

import lap
import numpy as np


def linear_assignment(cost_matrix, thresh):
    if cost_matrix.size == 0:
        return np.empty((0, 2), dtype=int), tuple(range(cost_matrix.shape[0])), tuple(range(cost_matrix.shape[1]))
    matches, unmatched_a, unmatched_b = [], [], []
    cost, x, y = lap.lapjv(cost_matrix, extend_cost=True, cost_limit=thresh)
    print(cost)
    for ix, mx in enumerate(x):
        if mx >= 0:
            matches.append([ix, mx])
    unmatched_a = np.where(x < 0)[0]
    unmatched_b = np.where(y < 0)[0]
    matches = np.asarray(matches)
    return matches, unmatched_a, unmatched_b


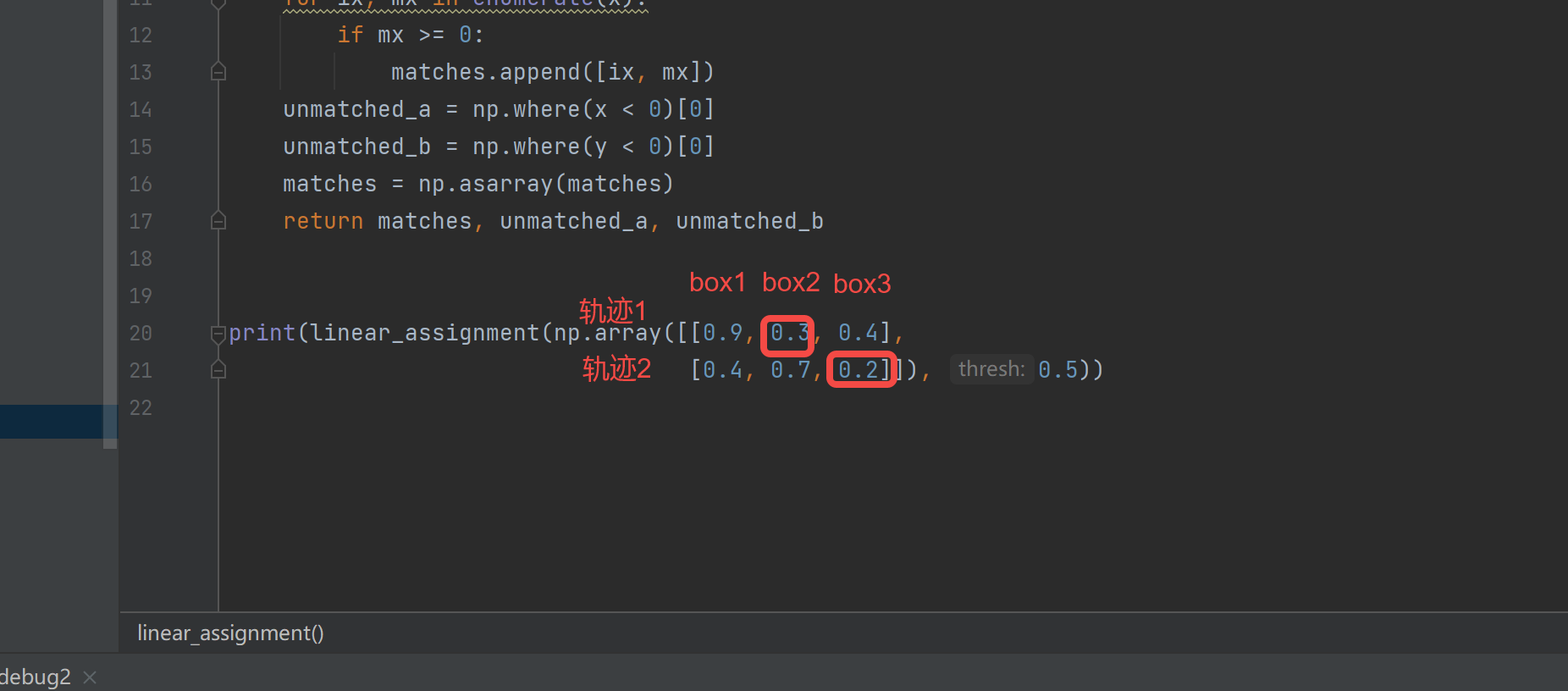
print(linear_assignment(np.array([[0.9, 0.3, 0.4],
                                  [0.4, 0.7, 0.2]]), 0.5))

输出：(array([[0, 1],
[1, 2]]), array([], dtype=int64), array([0], dtype=int64))

如果：

print(linear_assignment(np.array([[0.9, 0.3, 0.4, 0.3],
                                  [0.4, 0.7, 0.2, 0.3],
                                  [0.3, 0.5, 0.6, 0.3],]), 0.5))

输出：

0.8
(array([[0, 1],
       [1, 2],
       [2, 0]]), array([], dtype=int64), array([3], dtype=int64))

在Bytetrack中，所有轨迹和所有框都计算匹配得分，然后1减去匹配得分就是这里的分配代价矩阵。