全文下载链接:http://tecdat.cn/?p=27784
河源市是国务院1988年1月7日批准设立的地级市,为了深入研究河源市公路交通与经济发展的关系,本文选取了1988-2014年河源市建市以来24年的地区生产总值(GDP)和公路通车里程(GL)的时间序列数据,其中公路通车里程(GL)用来反映河源市公路交通发展状况,地区生产总值(GDP)反映河源市的经济增长状况(点击文末“阅读原文”获取完整代码数据)。
相关视频
为了消取数据的异方差,将原始数据取对数,分别记做LogGDP和LogGL,数据见表,采用ADF法对LogGDP和LogGL的平稳性进行单位根检验。
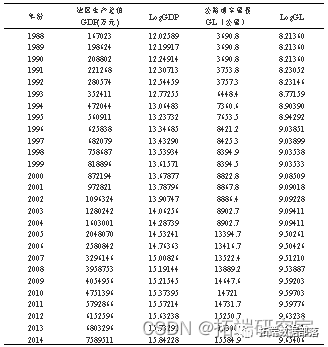
首先,对1988-2014年河源市24年的LogGDP和LogGL时间序列进行ADF单位根检验,单位根检验结果如表:
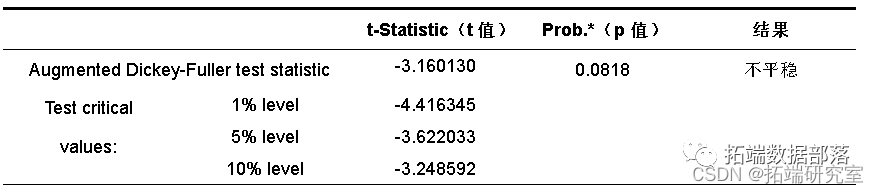
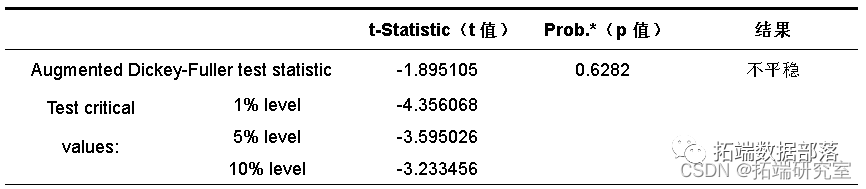
t值和p值是等效的,p值要求小于给定的显著水平,越小越好,小于0.05.等于0是最好的。结果显示,LogGDP和LogGL的ADF值分别为-3.160130和-1.895105,均大于水平值,说明接受原假设,LogGDP和LogGL序列存在单位根,为非平稳序列。因此,需要对LogGDP和LogGL序列继续第二步检验,即对LogGDP和LogGL的一阶差分进行检验,结果如表 :
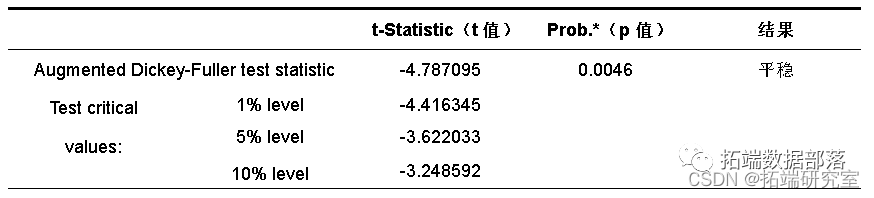
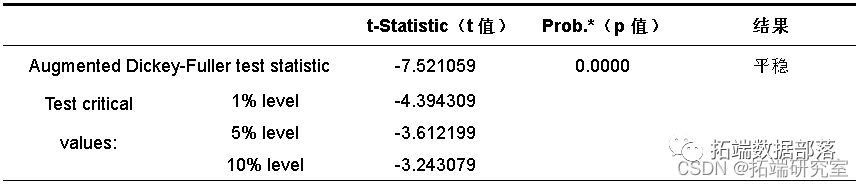
结果显示,LogGDP和LogGL经过一阶差分检验,得到一阶差分序列D(LogGDP)和D(LogGL)的p值分别为0.0046和 0.0000,均小于0.05的显著值。由于D(LogGDP)和D(LogGL)都是单整序列,且单整阶数相同,均为I(1),所以LogGDP和LogGL两序列之间可能存在协整关系。
点击标题查阅往期内容

向量自回归VAR的迭代多元预测估计 GDP 增长率时间序列|数据分享

左右滑动查看更多

01
02

03
04

GDP与公路交通里程GL协整性检验
由序列的平稳性检验结果可知,河源市地区生产总值GDP和公里通车里程GL在1988-2014年这个时间序列中可能存在协整关系,协整检验的方法有Engle Granger两步法和Johansen极大似然法前者适合对两变量的模型进行协整检验后者适合在多变量的VAR模型中进行检验。
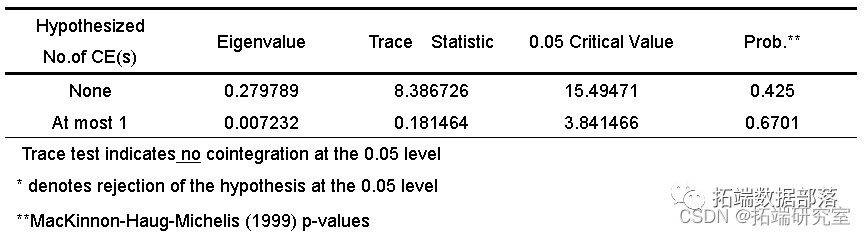
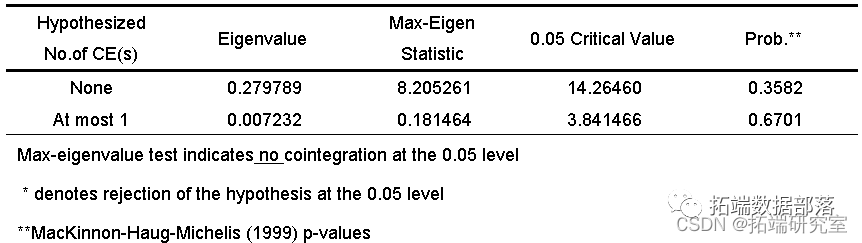
利用engle和granger提出的两步检验法:
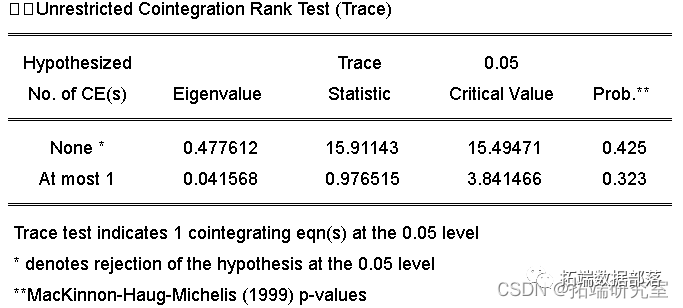
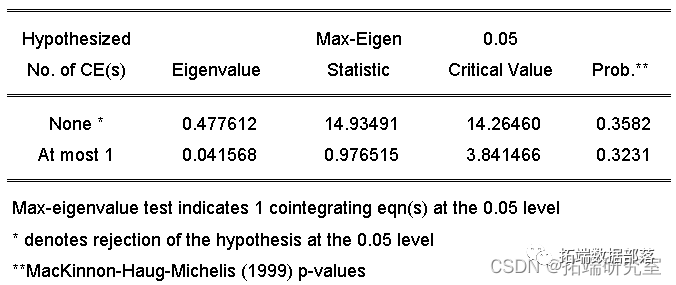
首先建立OLS回归模型,结果为
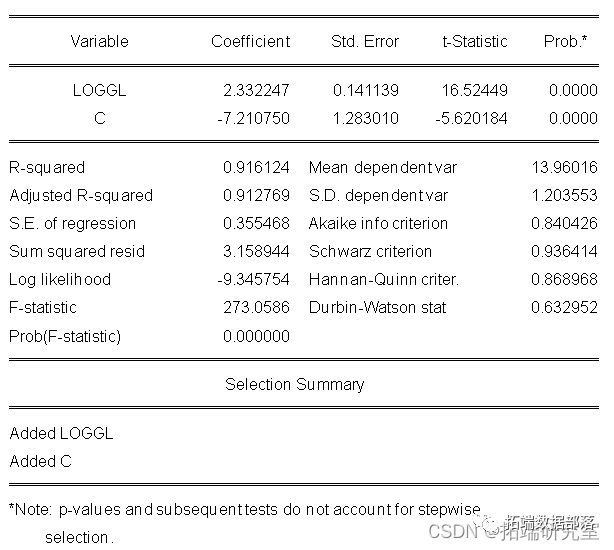
首先建立模型:y=ax+c+e,结果为loggdp= 2.332247*loggl + -7.210750
由ADF单位根检验结果可以看出上述变量是一阶平稳的符合granger因果关系检验的条件.现对各变量之间进行granger因果关系检验以确定它们之间的相互影响关系.取滞后阶数为2阶。
granger因果检验:
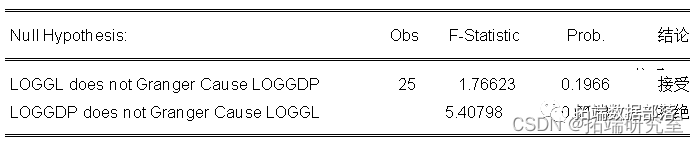
从结果可知拒绝loggl不能granger loggdp的假设,即loggl granger引起loggdp;但是不能拒绝loggdp不能granger引起loggl,即接受loggdp不能granger引起loggl。

同时,对方程的残差进行ADF检验结果可以看出残差序列不是平稳的,因此loggdp和loggl之间不存在协整关系。
建立VAR模型
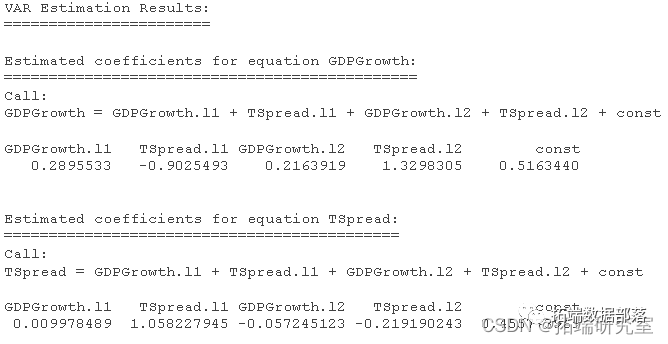
利用Eviews计量经济分析软件,本文对logGDP、loggl变量建立VAR(1)模型,对于VAR模型滞后阶数的选择,得到如表所列的5个评价指标,且5个指标均认为1阶合理即建立VAR(1)模型。
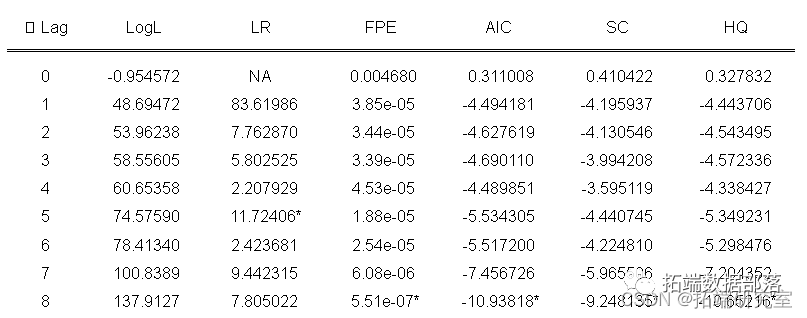
同时,有两类回归统计量出现在VAR对象估计输出的底部:

输出的第一部分的标准OLS回归统计量。根据各自的残差分别计算每个方程的结果,并显示在对应的列中。
输出的第二部分是VAR模型的回归统计量。
即协整方程式是:
LOGGDP=1.36534925116*LOGGDP(-1)-0.326349983643*LOGGDP(-2)+0.139864325278*LOGGL(-1)-0.239810823184*LOGGL(-2)+0.44758535991
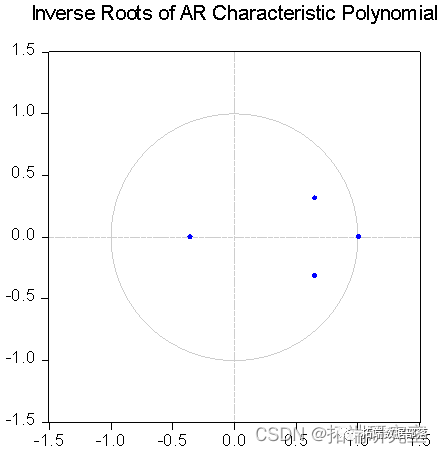
可以看到VAR模型的所有根模的倒数都小于1,即都在单位圆内,则该模型是稳定的。可以对VAR模型进行一个标准差的脉冲响应函数分析。
脉冲响应函数是用来衡量随机扰动项的一个标准差冲击对其他变量当前与未来取值的影响轨迹它能够比较直观地刻画变量之间的动态交互作用。
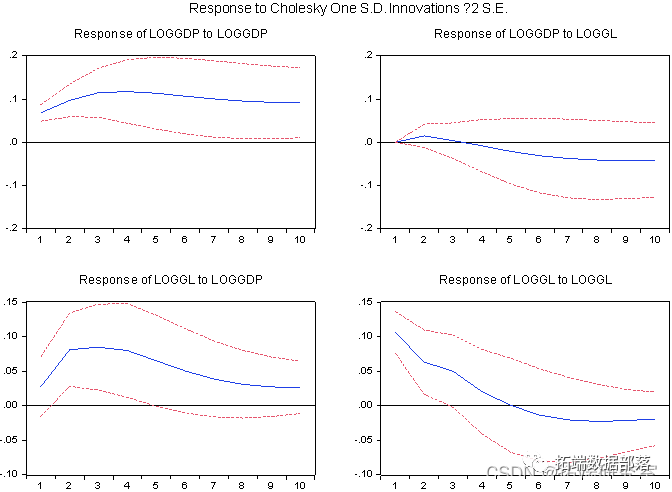
本文继续利用方差分解技术分析经济增长速度、交通量增长之间的相互贡献率。进行方差分解示意图。
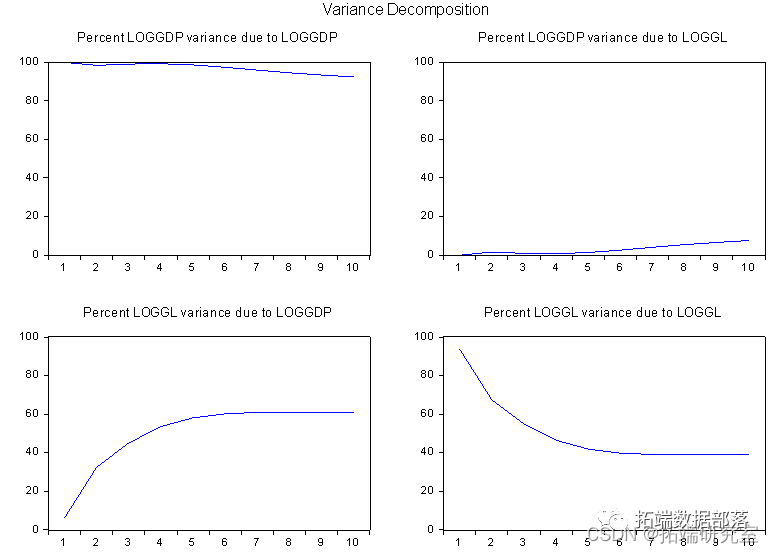
各变量对经济增长速度的贡献率。
实证检验
为了检验所建立交通量VAR预测模型的效果,用EVIEWS软件对loggdp历史数据仿真,得到如下预测模型。
loggdp = @coef(1) loggdp(-1) + @coef(2) loggdp(-2) + @coef(3) loggl(-1) + @coef(4) loggl(-2) + @coef(5)
@coef(1) = 1.3653493
@coef(2) = -0.3263500
@coef(3) = 0.1398643
@coef(4) = -0.2398108
@coef(5) = 0.4475854
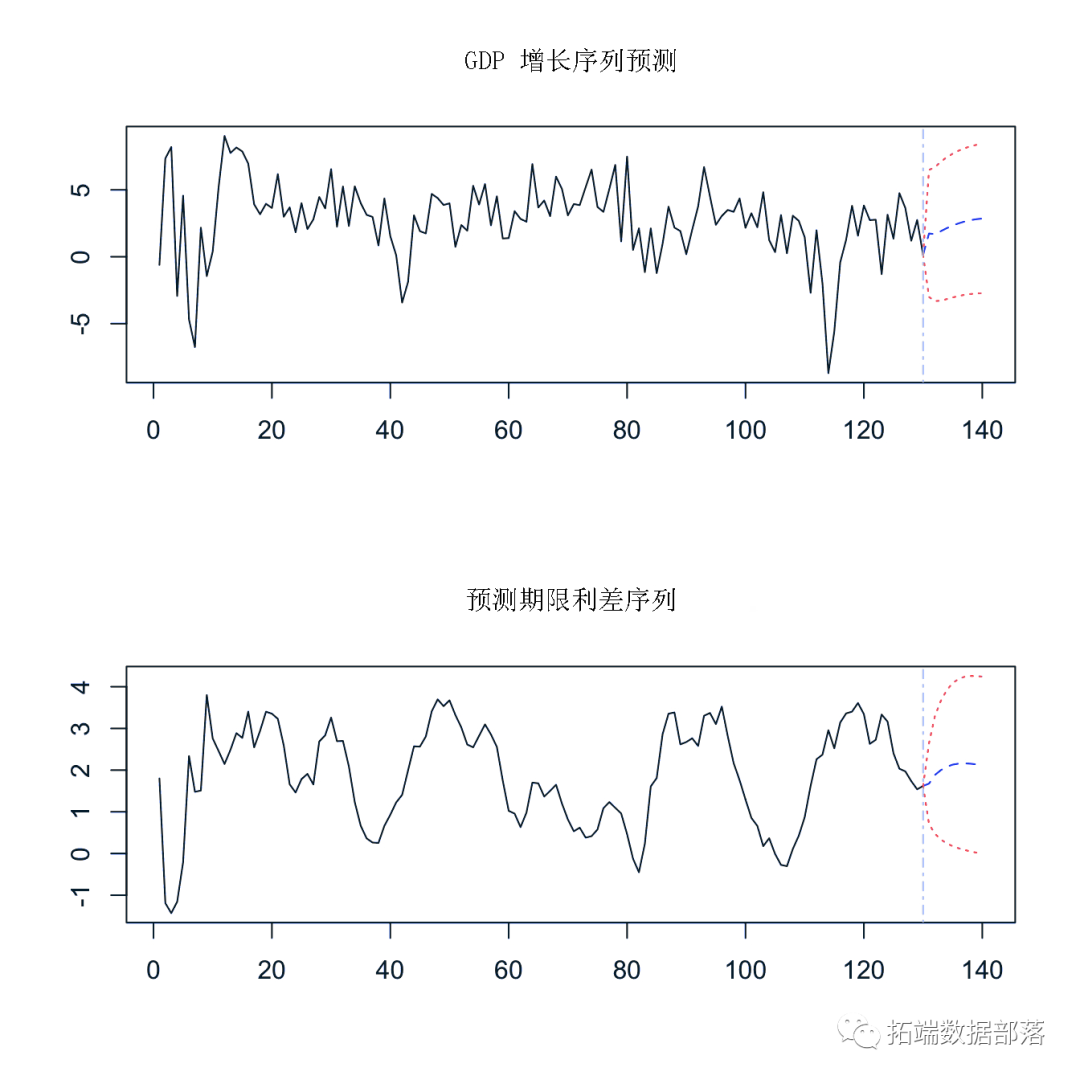
用VAR方法建立的GDP预测模型预测精度较高,效果较好。此外,可以得到如下的比较图:
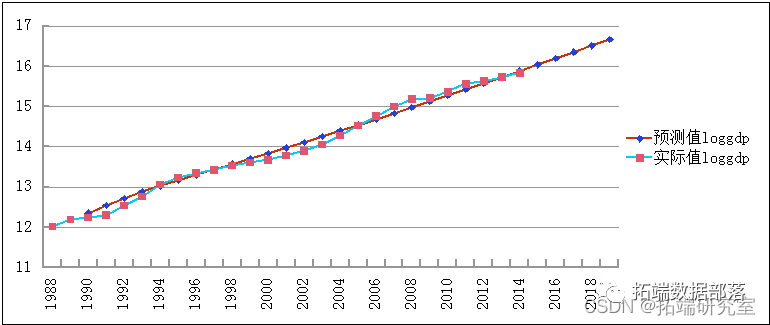
同时,对loggl历史数据仿真,得到如下预测模型。
loggl = @coef(1) loggdp(-1) + @coef(2) loggdp(-2) + @coef(3) loggl(-1) + @coef(4) loggl(-2) + @coef(5)
@coef(1) = 0.9502916
@coef(2) = -0.8089714
@coef(3) = 0.5952874
@coef(4) = -0.0153147
@coef(5) = 1.7812591
以及历年loggl预测值、loggl实际值。
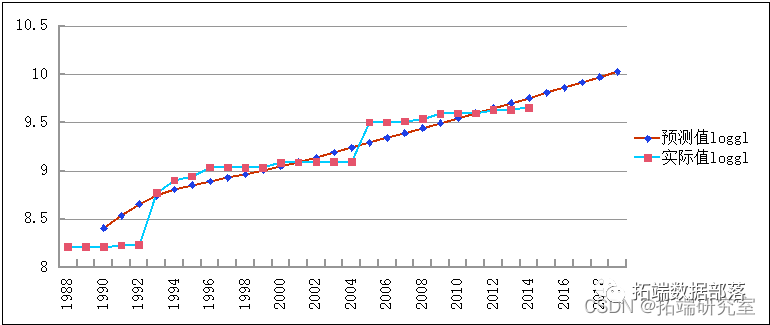
采用VAR方法建立的GDP预测模型有一个显著优点,即它不用对当期的GDP或其他变量作出预测,只用历史的GDP和交通量数据,就可以对GDP做出比较准确的预测,由于减少中间变量预测的传递,相应提高了模型预测精度。

点击文末“阅读原文”
获取全文完整资料。
本文选自《Eviews用向量自回归模型VAR实证分析公路交通通车里程与经济发展GDP协整关系时间序列数据和脉冲响应可视化》。


点击标题查阅往期内容
R语言实现向量自回归VAR模型
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
向量自回归(VAR)模型分析消费者价格指数 (CPI) 和失业率时间序列
Matlab创建向量自回归(VAR)模型分析消费者价格指数 (CPI) 和失业率时间序列
Stata广义矩量法GMM面板向量自回归 VAR模型选择、估计、Granger因果检验分析投资、收入和消费数据
R语言时变向量自回归(TV-VAR)模型分析时间序列和可视化
R语言用向量自回归(VAR)进行经济数据脉冲响应研究分析
R语言arima,向量自回归(VAR),周期自回归(PAR)模型分析温度时间序列
R语言VAR模型的不同类型的脉冲响应分析
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
R语言时变参数VAR随机模型
R语言估计时变VAR模型时间序列的实证研究分析案例
R语言向量自回归模型(VAR)及其实现
R语言实现向量自回归VAR模型
R语言估计时变VAR模型时间序列的实证研究分析案例
Python和R用EWMA,ARIMA模型预测时间序列
R语言用LASSO,adaptive LASSO预测通货膨胀时间序列
Python中的ARIMA模型、SARIMA模型和SARIMAX模型对时间序列预测
R语言arima,向量自回归(VAR),周期自回归(PAR)模型分析温度时间序列
【视频】Python和R语言使用指数加权平均(EWMA),ARIMA自回归移动平均模型预测时间序列

![]()