排序数组

难度：中等

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

计数排序

思路：
计数排序是一个排序是不比较元素大小的排序算法。

计数排序对一定范围内的整数排序时候的速度非常快，一般快于其他排序算法。但计数排序局限性比较大，只限于对整数进行排序，而且待排序元素值分布较连续、跨度小的情况。

如果一个数组里所有元素都是整数，而且都在0-K以内。那对于数组里每个元素来说，如果能知道数组里有多少项小于或等于该元素，就能准确地给出该元素在排序后的数组的位置。

计数排序（升序）样例：

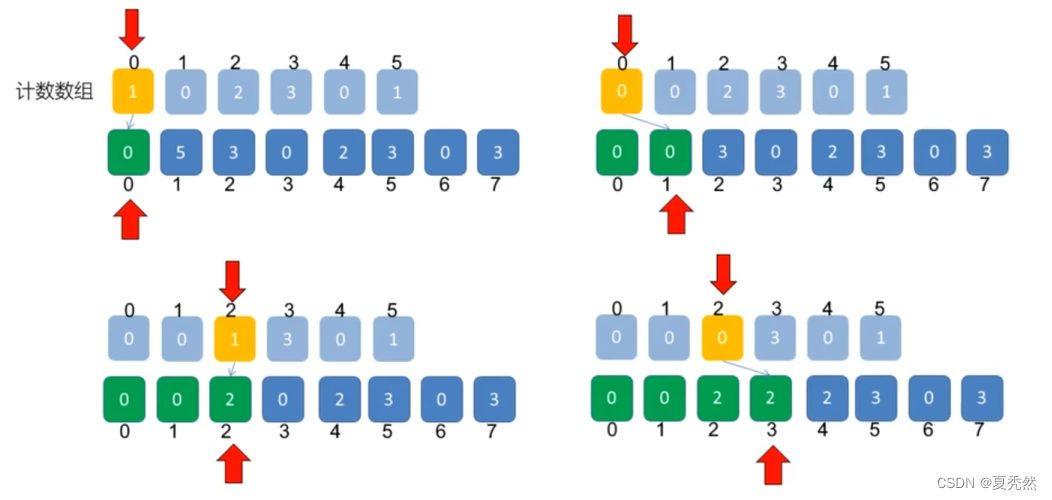
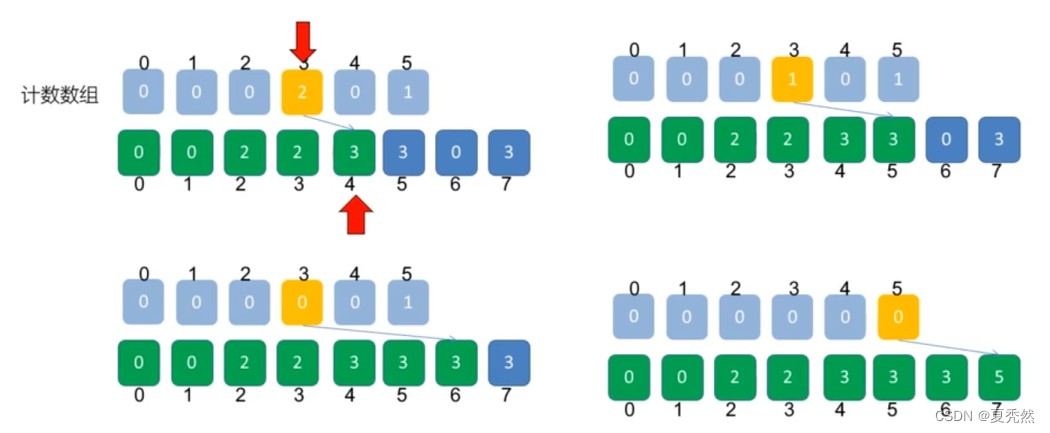
实际应用中我们会同时找出数组中的 max 和 min ，主要是为了尽量节省空间。试想 [1003,1001,1030,1050] 这样的数据要排序，真的需要建立长度为1050+1 的数组吗?我们只需要长度为 1050-1003+1=48 的数组(先不考虑额外 +1 的长度)，就能囊括从最小到最大元素之间的所有元素了。

如果待排序数组的元素值跨度很大，比如 [99999,1,2]，为三个元素排序要使用 99999-1+1 的空间，实在是浪费。所以计数排序适用于待排序元素值分布较连续、跨度小的情况。

时间复杂度： $O(n+M)$，其中 $n$ 是数组长度，$M$ 是 $max$ - $min$ + 1。
空间复杂度： $O(M)$，$M$ 是 $max$ - $min$ + 1。

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        nums_min, nums_max = min(nums), max(nums)
        # 构建计数数组
        nums_count = [0 for i in range(nums_max - nums_min + 1)]
        for i in nums:
            nums_count[i - nums_min] += 1
        # 通过计数数组转换完成排序
        index = 0
        for j, x in enumerate(nums_count):
            if x:
                nums[index: index+x] = [j + nums_min] * x
                index += x
        return nums

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/sort-an-array