一、正向代理和反向代理
🚩正向代理和反向代理是两种常见的代理服务器模式,用于在网络通信中起到中介的作用。
🏴正向代理(Forward Proxy):
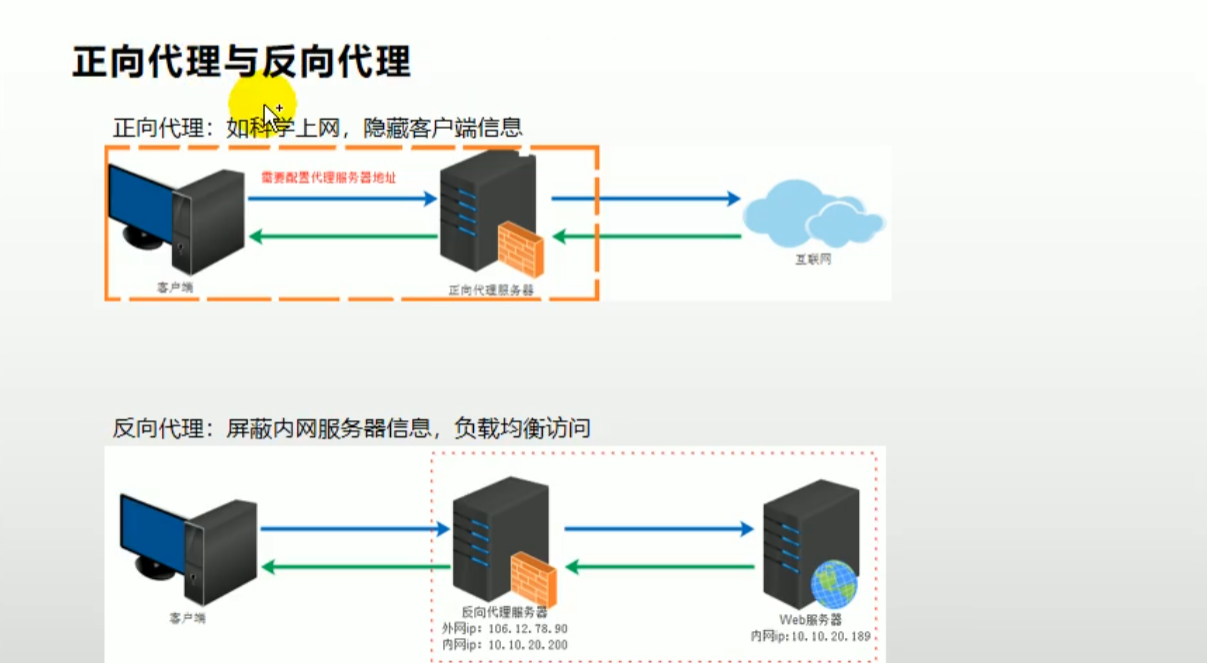
正向代理是在客户端和目标服务器之间充当中介的代理服务器。客户端向正向代理发送请求,然后代理服务器将请求转发给目标服务器,并将目标服务器的响应返回给客户端。正向代理隐藏了客户端的真实身份,并可以提供一些额外的功能,如访问控制、缓存、安全性等。典型的应用场景包括vpn工具等。
🏴☠️反向代理(Reverse Proxy):
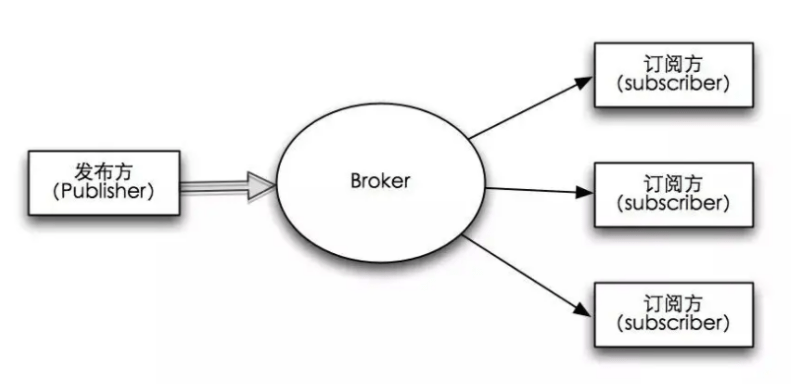
反向代理是在目标服务器和客户端之间充当中介的代理服务器。客户端向反向代理发送请求,然后反向代理根据一定的规则将请求转发给后端的目标服务器,并将后端服务器的响应返回给客户端。反向代理可以提供负载均衡、缓存、SSL 加密、安全防护等功能。典型的应用场景包括网站负载均衡、HTTPS 代理、Web 应用防火墙等。
🏳🌈正向代理和反向代理的主要区别在于代理服务器的位置和作用对象。正向代理隐藏了客户端的真实身份,代表客户端发送请求;而反向代理则隐藏了目标服务器的真实身份,代表服务器接收请求。两者都可以提高系统的性能、安全性和可靠性,并广泛应用于网络环境中。
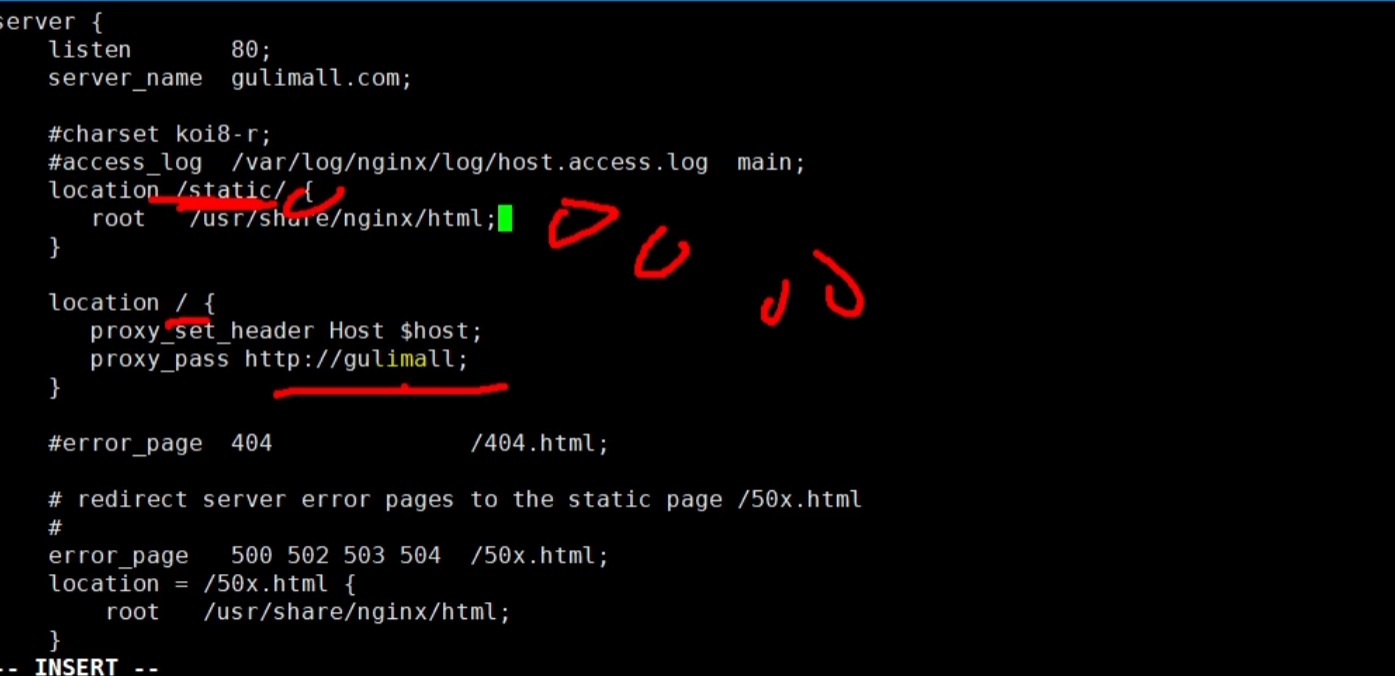
二、配置
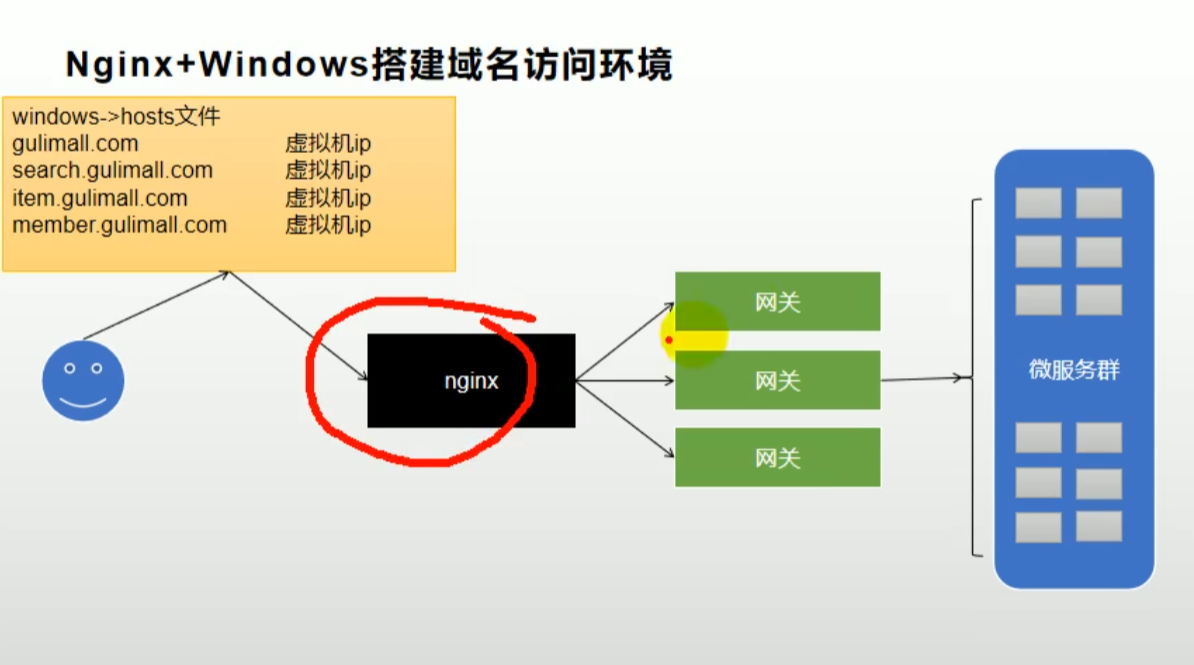
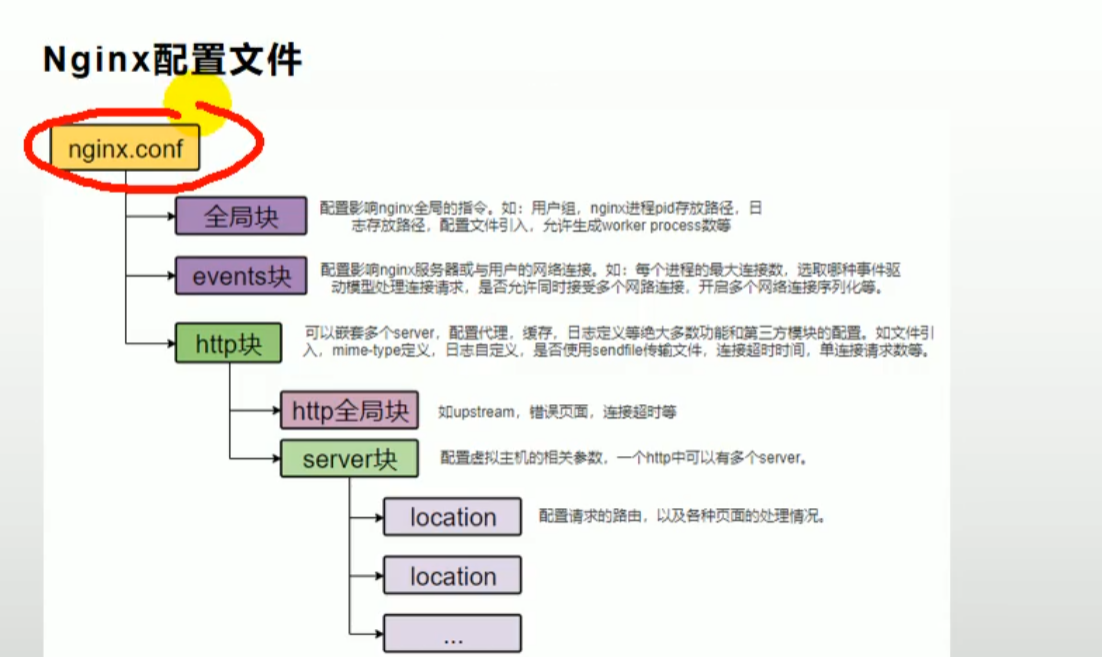
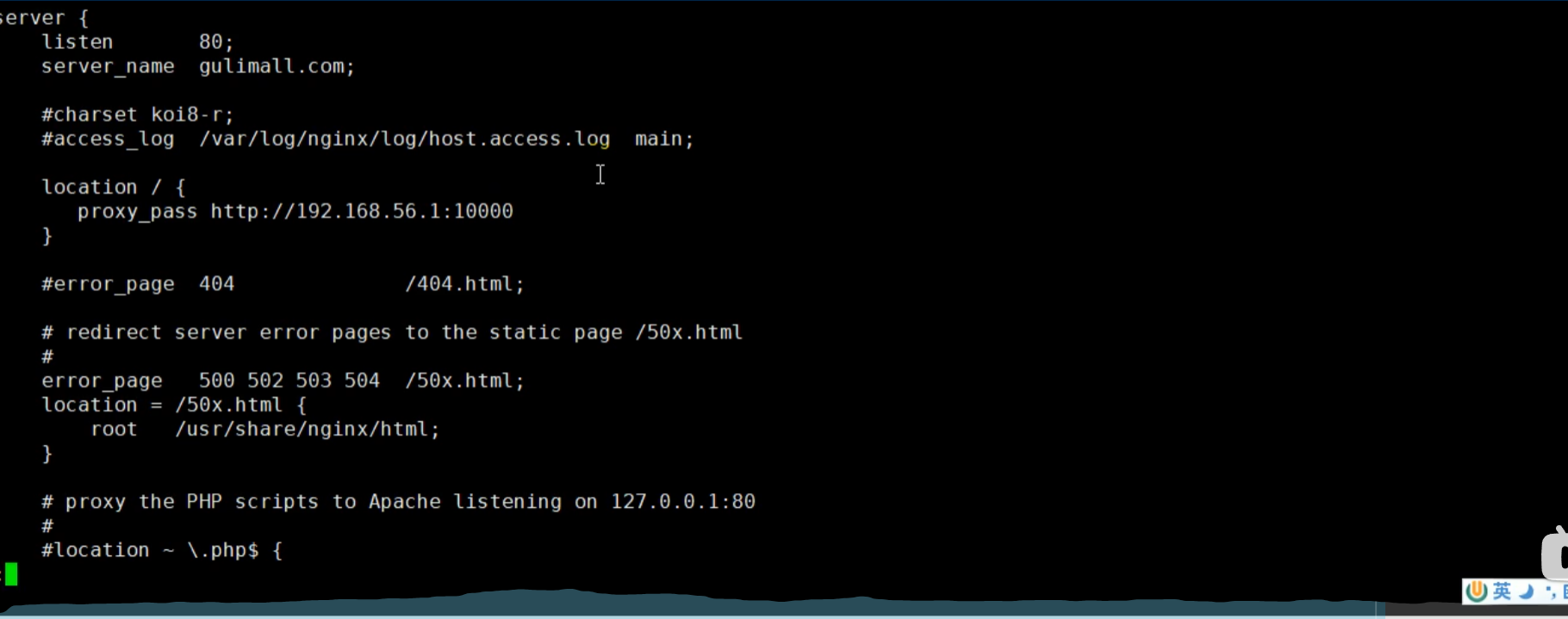
三、配置负载均衡
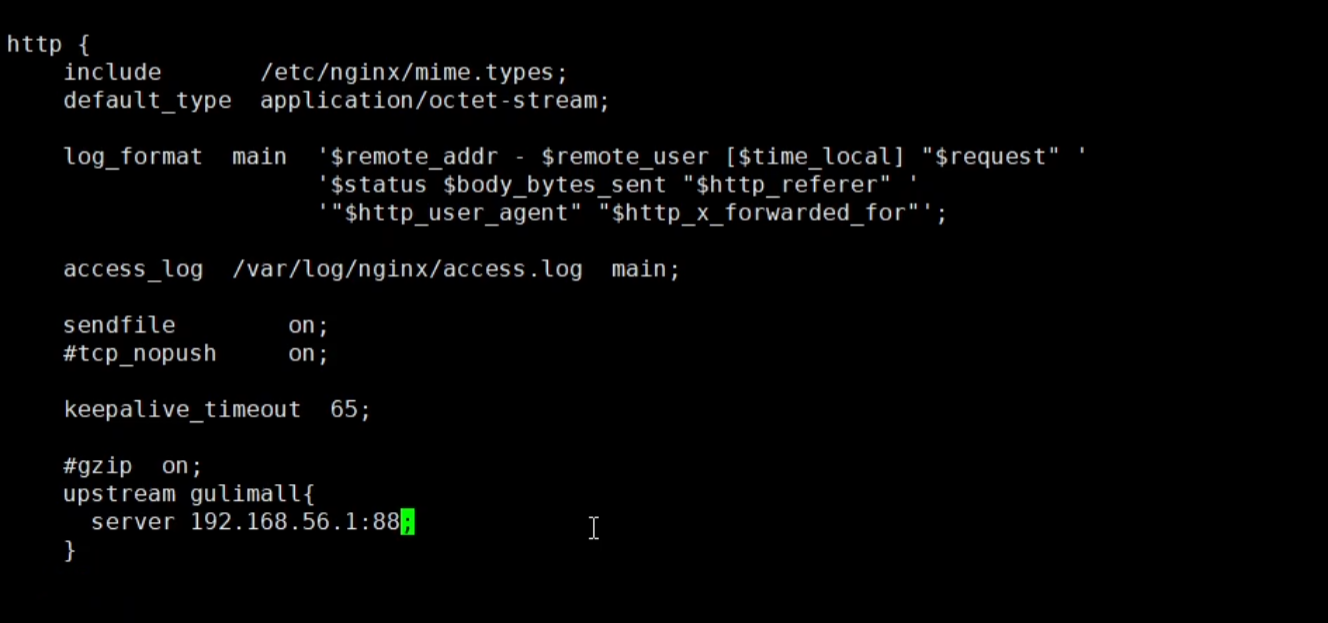
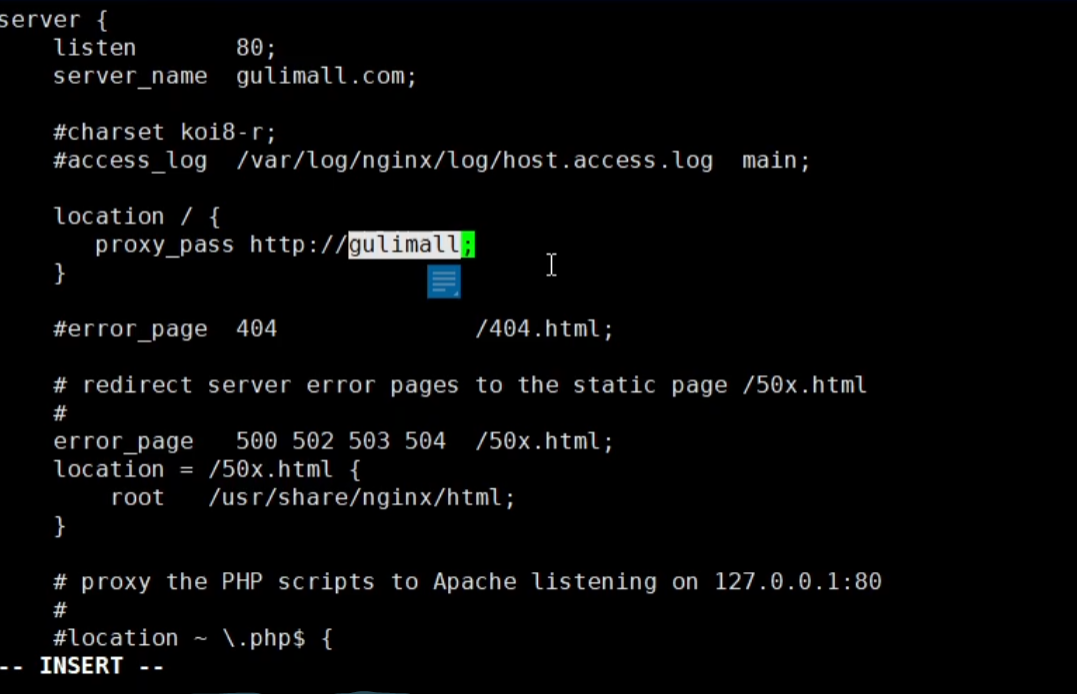
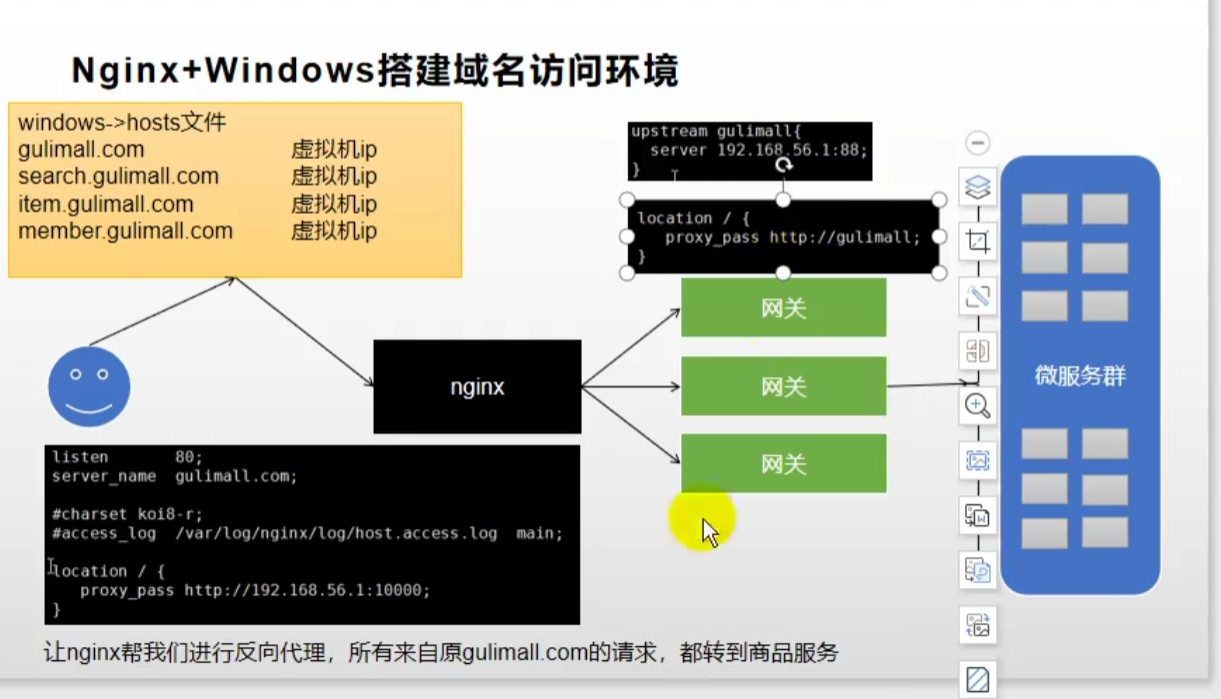
再给网关配上路由规则
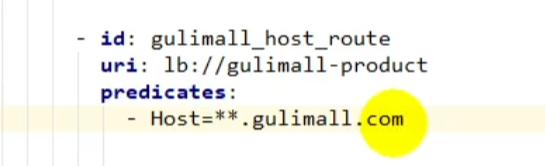
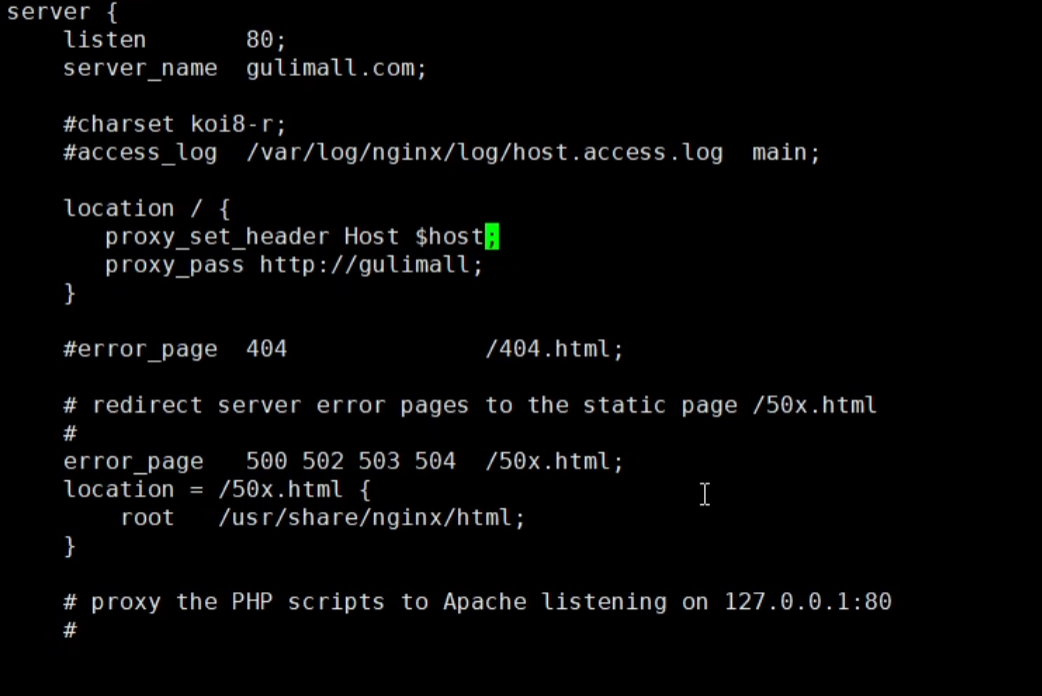
但是还有一个坑,就是nginx代理给网关的时候,会丢失请求的host信息
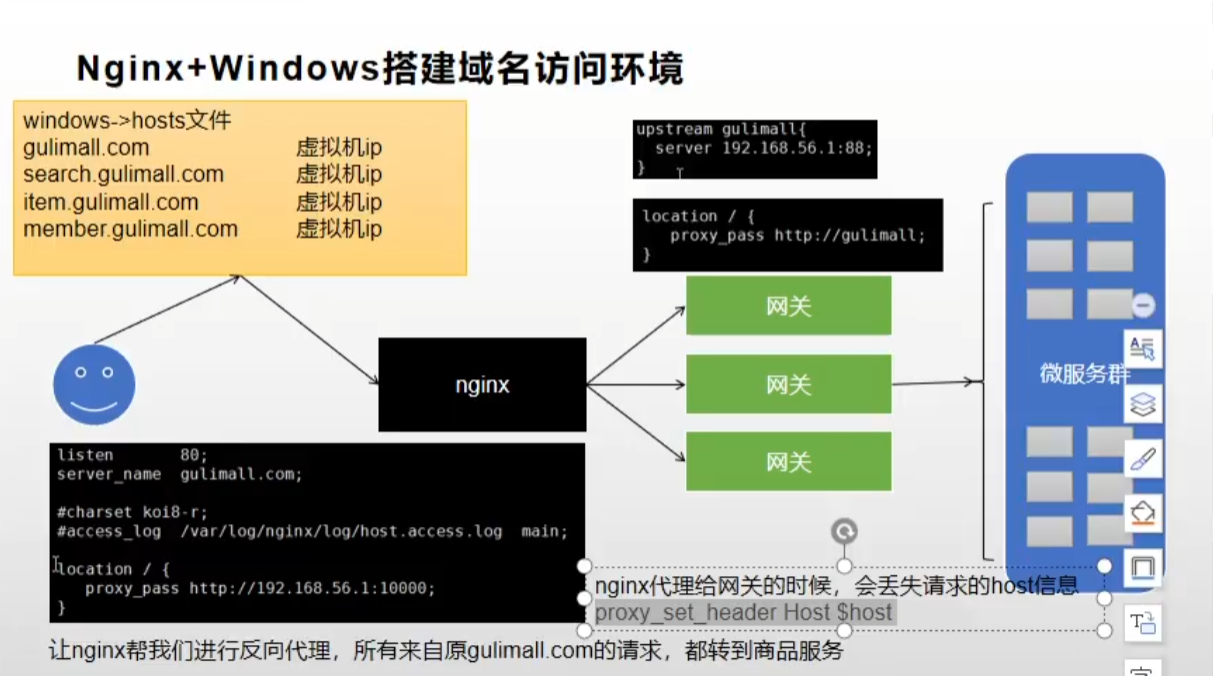
四、动静分离