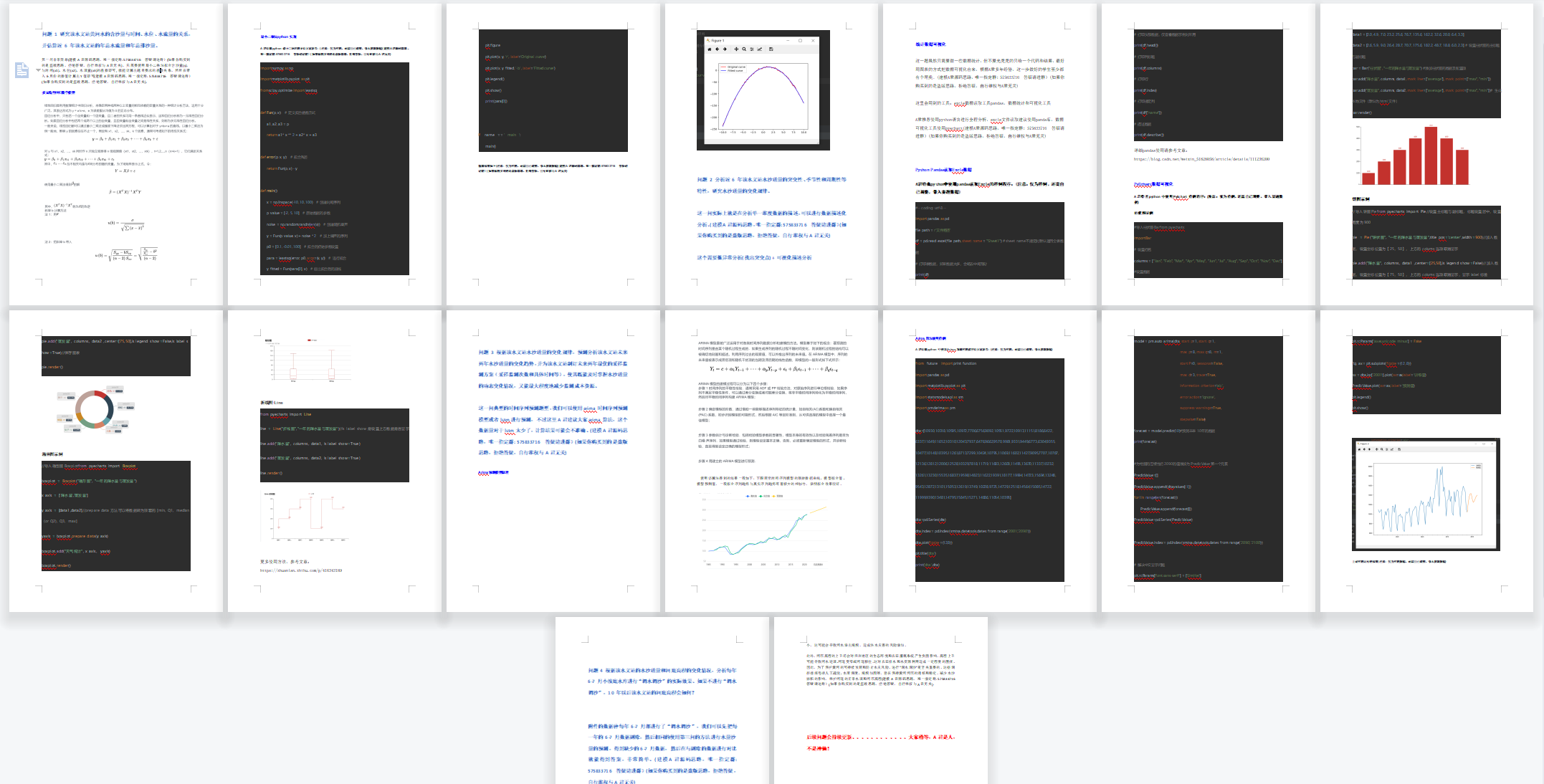
509. 斐波那契数
//法一:
/**
* @param {number} n
* @return {number}
*/
var fib = function(n) {
let bp=new Array(n)
bp[0]=0
bp[1]=1
for(let i=2;i<=n;i++){
bp[i]=bp[i-1]+bp[i-2]
}
return bp[n]
};
//法二,时间少,空间少,只需要维护两个数值就可以了,不需要记录整个序列。
/**
* @param {number} n
* @return {number}
*/
var fib = function(n) {
if (n == 0) return 0;
if (n == 1) return 1;
let sum = 0;
let prev1 = 0;
let prev2 = 1;
for (let i = 1; i < n; i++) {
sum = prev1 + prev2;
prev1 = prev2;
prev2 = sum;
}
return sum;
};
70. 爬楼梯
/**
* @param {number} n
* @return {number}
*/
var climbStairs = function(n) {
//2+bp(n-1)+bp(n-2)
let bp=new Array(n+1)
bp[1]=1
bp[2]=2
for(let i=3;i<=n;i++){
bp[i]=bp[i-1]+bp[i-2]
}
return bp[n]
};
第一想法
2+bp(n-1)+bp(n-2)
比如有10步楼梯=1步+9步楼梯的方法+2步+8步楼梯的方法
746. 使用最小花费爬楼梯
/**
* @param {number[]} cost
* @return {number}
*/
var minCostClimbingStairs = function(cost) {
let n=cost.length
let dp=new Array(n)
// dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
dp[0]=0
dp[1]=0
for(let i=2;i<=n;i++){
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[n]
function min(a,b){
return a>b?b:a
}
};
想法
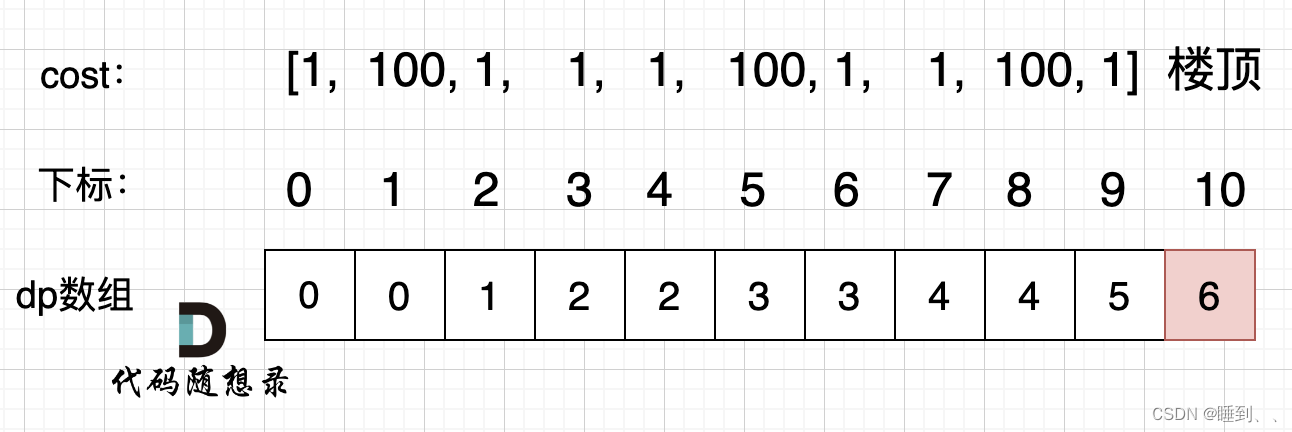
-
确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,大家一定要清晰! -
确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]); -
dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
1
/**
* @param {number[]} nums
* @return {number[]}
*/