LQR(Linear Quadratic Regulator)控制器
LQR(Linear Quadratic Regulator)是一种经典的线性控制器设计方法,用于设计线性时不变系统的状态反馈控制器,以最小化系统性能指标,通常是二次代价函数。下面,将详细推导LQR算法,并提供MATLAB应用示例。
推导LQR控制器:
考虑一个离散时间线性时不变系统的状态空间表达式:
x [ k + 1 ] = A x [ k ] + B u [ k ] x[k+1] = A x[k] + B u[k] x[k+1]=Ax[k]+Bu[k]
其中, x [ k ] x[k] x[k] 是系统状态, u [ k ] u[k] u[k] 是控制输入, A A A 和 B B B 是系统矩阵。
LQR的目标是找到一个状态反馈控制器,它具有以下形式:
u [ k ] = − K x [ k ] u[k] = -K x[k] u[k]=−Kx[k]
其中, K K K 是控制器增益矩阵,它需要优化。控制器的目标是最小化以下代价函数:
J = ∑ k = 0 ∞ ( x [ k ] T Q x [ k ] + u [ k ] T R u [ k ] ) J = \sum_{k=0}^{\infty} (x[k]^T Q x[k] + u[k]^T R u[k]) J=k=0∑∞(x[k]TQx[k]+u[k]TRu[k])
其中, Q Q Q 是状态权重矩阵, R R R 是控制输入权重矩阵。
我们首先需要解出Riccati方程来找到最优控制器增益 K K K和最小的代价函数 J J J。
- 首先,我们定义代价函数的无穷时间累积:
J = lim N → ∞ ∑ k = 0 N ( x [ k ] T Q x [ k ] + u [ k ] T R u [ k ] ) J = \lim_{N\to\infty}\sum_{k=0}^{N} (x[k]^T Q x[k] + u[k]^T R u[k]) J=N→∞limk=0∑N(x[k]TQx[k]+u[k]TRu[k])
- 接下来,我们定义一个有限时间的代价函数,称为 J N J_N JN,并将其表示为与无穷时间代价函数的差值:
J N = ∑ k = 0 N ( x [ k ] T Q x [ k ] + u [ k ] T R u [ k ] ) − x [ N + 1 ] T Q x [ N + 1 ] J_N = \sum_{k=0}^{N} (x[k]^T Q x[k] + u[k]^T R u[k]) - x[N+1]^T Q x[N+1] JN=k=0∑N(x[k]TQx[k]+u[k]TRu[k])−x[N+1]TQx[N+1]
这里,我们假设 x [ N + 1 ] x[N+1] x[N+1]是一个零向量,这是因为我们在有限时间内考虑代价。
- 然后,我们通过对 J N J_N JN对 u [ k ] u[k] u[k]求偏导,并令其等于零来找到最小值:
∂ J N ∂ u [ k ] = 2 R u [ k ] + 2 B T P x [ k ] = 0 \frac{\partial J_N}{\partial u[k]} = 2R u[k] + 2B^T P x[k] = 0 ∂u[k]∂JN=2Ru[k]+2BTPx[k]=0
其中, P P P是状态权重矩阵的解,它满足离散时间的Riccati方程:
P = A T P A − A T P B ( R + B T P B ) − 1 B T P A + Q P = A^T P A - A^T P B (R + B^T P B)^{-1} B^T P A + Q P=ATPA−ATPB(R+BTPB)−1BTPA+Q
- 一旦我们找到了 P P P,我们可以计算最优控制器增益 K K K:
K = ( R + B T P B ) − 1 B T P A K = (R + B^T P B)^{-1} B^T P A K=(R+BTPB)−1BTPA
步骤4:使用MATLAB实现LQR控制器和仿真
以下是针对一个二阶系统的MATLAB代码示例,包括控制器设计和性能仿真。假设我们有以下系统参数:
A = [ 1 1 0 1 ] , B = [ 0 1 ] , Q = [ 1 0 0 1 ] , R = 1 A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \quad Q = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad R = 1 A=[1011],B=[01],Q=[1001],R=1
% 定义系统矩阵
% 系统矩阵
A = [1, 1; 0, 1];
B = [0; 1];
% 权重矩阵
Q = [1, 0; 0, 1];
R = 1;
% 求解Riccati方程
P = dare(A, B, Q, R);
% 计算最优控制器增益矩阵 K
K = (R + B' * P * B)^(-1) * B' * P * A;
% 仿真系统响应
x0 = [100; 0]; % 初始状态
N = 100; % 仿真步数
x = zeros(2, N);
u = zeros(1, N);
x(:,1) =x0;
for k = 1:N
u(k) = -K * x(:, k); % 计算控制输入
x(:, k+1) = A * x(:, k) + B * u(k); % 更新状态
end
% 绘制状态和控制输入
figure(Color='w')
t = 0:N;
subplot(2, 1, 1);
plot(t, x(1, :), 'b', 'LineWidth', 2);
ylabel('状态 x_1');
title('LQR控制器仿真');
set(gca,'FontSize',18);
subplot(2, 1, 2);
stairs(t(1:end-1), u, 'r', 'LineWidth', 2);
xlabel('时间步骤');
ylabel('控制输入 u');
set(gca,'FontSize',18);
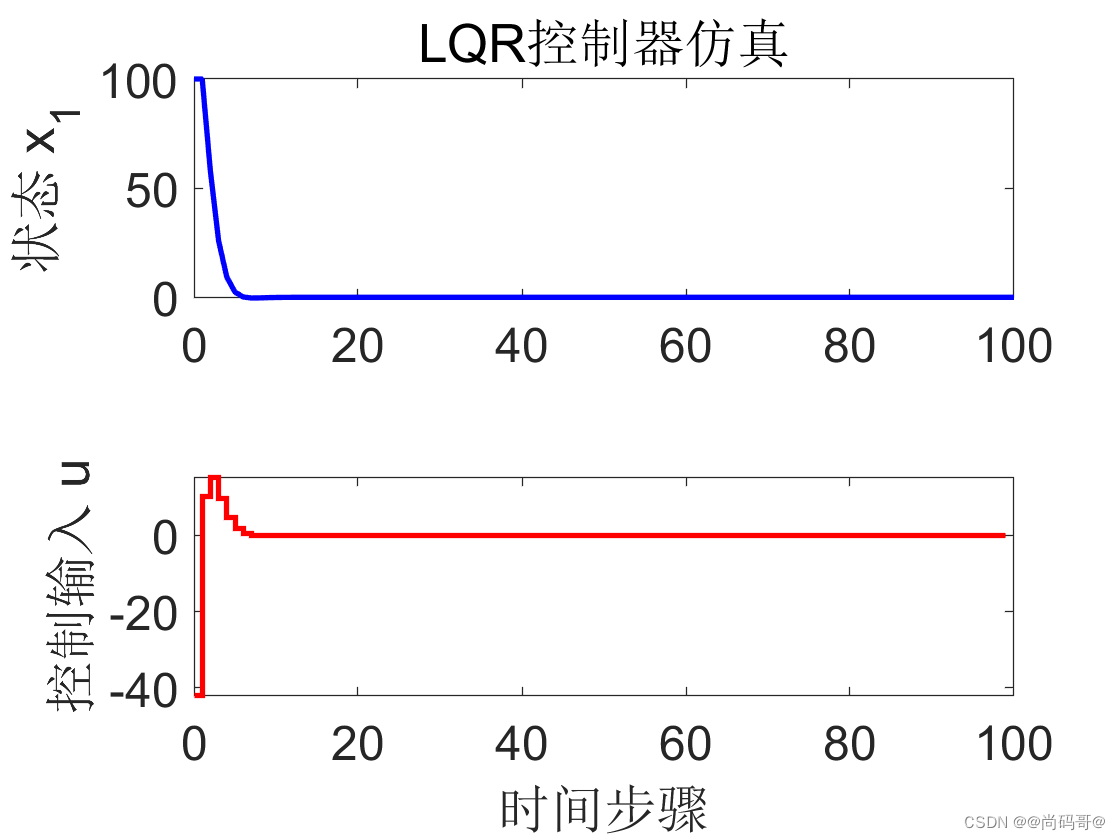
在这个示例中,我们首先定义了系统的
A
A
A和
B
B
B矩阵,然后设置了状态权重矩阵
Q
Q
Q和控制输入权重矩阵
R
R
R。接下来,我们使用dare函数来解Riccati方程,找到状态权重矩阵
P
P
P,然后计算最优控制器增益矩阵
K
K
K。这个矩阵
K
K
K可以用于状态反馈控制系统。