前置知识

参考前文

参考文章：
LeetCode刷题笔记【29】：动态规划专题-1（斐波那契数、爬楼梯、使用最小花费爬楼梯）

62.不同路径

题目描述

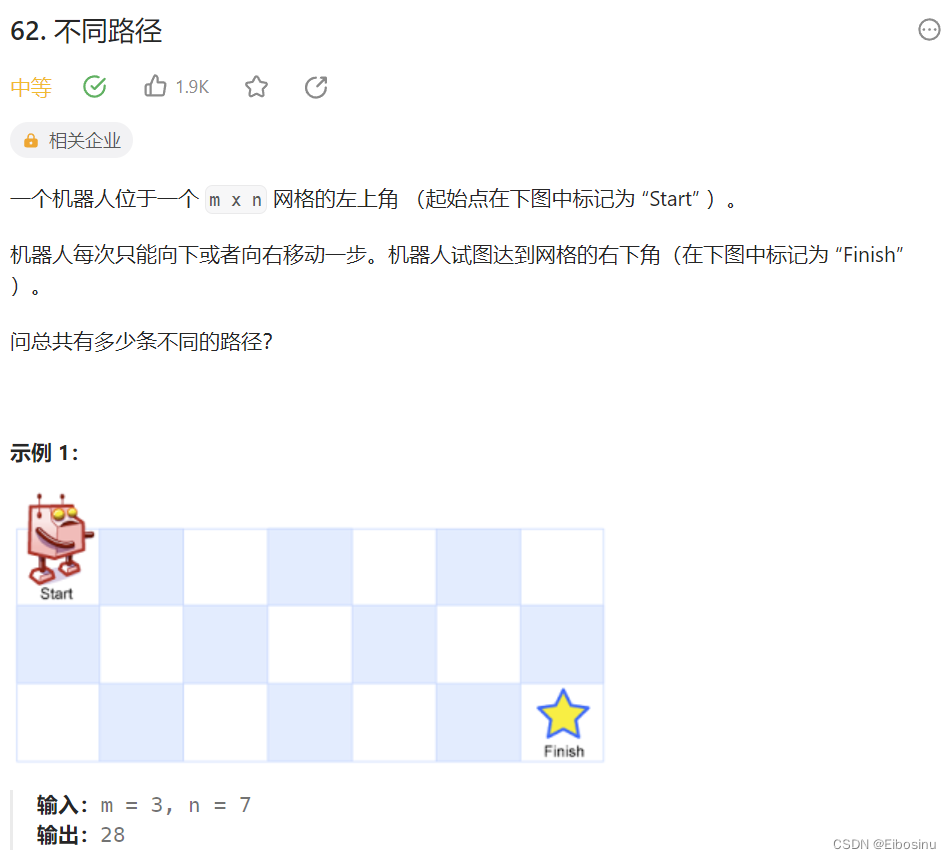
LeetCode链接：https://leetcode.cn/problems/unique-paths/description/

解题思路

动态规划: 创建m×n的数组, 对应这个地图, 数组val表示有几种方法可以走到这一格
最开始, 第一行和第一列val都是1, 然后依次遍历更新val
每一格的val是其上和左格子的和

代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> map(m, vector<int>(n));
        for(int i=0; i<n; i++){
            map[0][i] = 1;
        }
        for(int i=0; i<m; i++){
            map[i][0] = 1;
        }
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                map[i][j] = map[i-1][j] + map[i][j-1];
            }
        }
        return map[m-1][n-1];
    }
};

63. 不同路径 II

题目描述

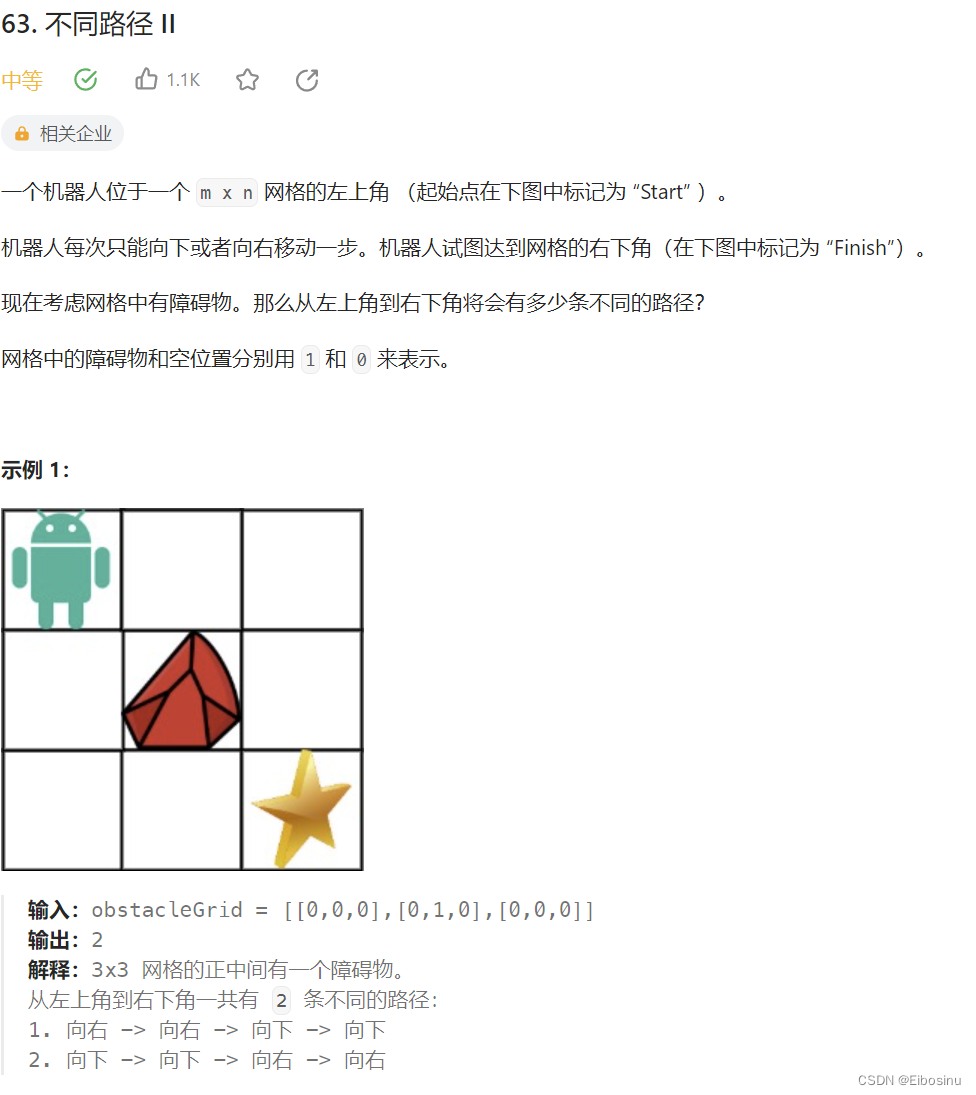
LeetCode链接：https://leetcode.cn/problems/unique-paths-ii/description/

障碍信息传递法(比较复杂)

参考<62. 不同路径>
动态规划, 先把石头初始化为INT_MAX(并且初始化过程中前面一个是INT_MAX, 那他自己也是INT_MAX)

递推遍历的过程中加一个判断
① 如果左和上都是INT_MAX, 那么本位置也是INT_MAX
② 如果上/左有一个是INT_MAX, 那么val是另一个非INT_MAX的
③ 正常递推

class Solution {
private:
    int maxNum = INT_MAX;
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        for(int i=0; i<obstacleGrid.size(); ++i){
            for(int j=0; j<obstacleGrid[0].size(); ++j){
                if(obstacleGrid[i][j]==1)
                    obstacleGrid[i][j] = maxNum;
            }
        }

        if(obstacleGrid[0][0] != maxNum)
            obstacleGrid[0][0] = 1;
        for(int i=1; i<obstacleGrid[0].size(); ++i){
            if(obstacleGrid[0][i-1]==maxNum)
                obstacleGrid[0][i] = maxNum;
            if(obstacleGrid[0][i] != maxNum)
                obstacleGrid[0][i] = 1;
        }
        for(int i=1; i<obstacleGrid.size(); ++i){
            if(obstacleGrid[i-1][0]==maxNum)
                obstacleGrid[i][0] = maxNum;
            if(obstacleGrid[i][0] != maxNum)
                obstacleGrid[i][0] = 1;
        }

        for(int i=1; i<obstacleGrid.size(); ++i){
            for(int j=1; j<obstacleGrid[0].size(); ++j){
                if(obstacleGrid[i][j]==maxNum)
                    continue;
                int left = obstacleGrid[i-1][j];
                int over = obstacleGrid[i][j-1];
                if(left==maxNum && over==maxNum){
                    obstacleGrid[i][j] = maxNum;
                }else if(left==maxNum || over==maxNum){
                    obstacleGrid[i][j] = min(left, over);
                }else{
                    obstacleGrid[i][j] = left + over;
                }
            }
        }

        if(obstacleGrid.back().back()==maxNum)
            return 0;
        else
            return obstacleGrid.back().back();
    }
};

这样做相当于是如果在过程中遇到了障碍物, 就把这个障碍物的信息继续往后传递, 一直到遍历结束.

这样当然可以解决问题, 并且整个遍历的过程也非常符合手工推导的直觉.
但是落实到代码层面的话, 不管是初始化的过程, 推导的过程, 还是最后得出结果的步骤, 都会变得更加繁琐, 不够简洁.

被障碍物阻挡后直接清空计数法(更简洁)

另一种思路: 将obstacleGrid试做参考, 自己新建一个map;

在遍历过程中如果当前位置有障碍物, 那么就直接给当前位置赋值0(清空前面的累计计数);
其含义也可以理解为: 有0种方法可以走到当前位置.

在初始化时, 遇到障碍物, 直接停止初始化.

class Solution {
private:
    int maxNum = INT_MAX;
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        if(obstacleGrid[0][0]==1 || obstacleGrid[m-1][n-1]==1)//一些trick, 起点终点处有障碍物就没法走了
            return 0;
        vector<vector<int>> map(m, vector<int>(n));
        for(int i=0; i<n; i++){
            if(obstacleGrid[0][i]==1)
                break;
            map[0][i] = 1;
        }
        for(int i=0; i<m; i++){
            if(obstacleGrid[i][0]==1)
                break;
            map[i][0] = 1;
        }
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                if(obstacleGrid[i][j]==1)
                    continue;
                map[i][j] = map[i-1][j] + map[i][j-1];
            }
        }
        return map[m-1][n-1];
    }
};