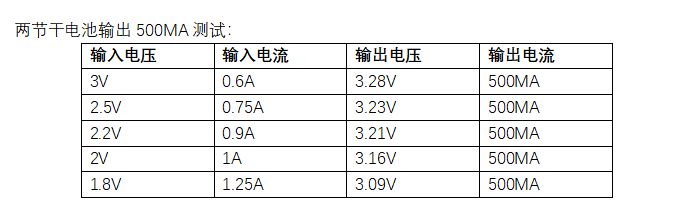
In geometry, Heron’s formula (or Hero’s formula) gives the area A of a triangle in terms of the three side lengths a, b, c. If {\textstyle s={\tfrac {1}{2}}(a+b+c)}{\textstyle s={\tfrac {1}{2}}(a+b+c)} is the semiperimeter of the triangle, the area is,[1]

{\displaystyle A={\sqrt {s(s-a)(s-b)(s-c)}}.}A={\sqrt {s(s-a)(s-b)(s-c)}}.
It is named after first-century engineer Heron of Alexandria (or Hero) who proved it in his work Metrica, though it was probably known centuries earlier.

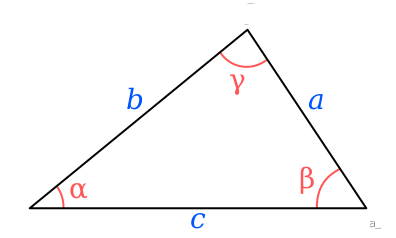
A triangle with sides a, b, and c

1 Example

Let △ABC be the triangle with sides a = 4, b = 13 and c = 15. This triangle’s semiperimeter is

{\displaystyle s={\frac {a+b+c}{2}}={\frac {4+13+15}{2}}=16}{\displaystyle s={\frac {a+b+c}{2}}={\frac {4+13+15}{2}}=16}
and so the area is

{\displaystyle {\begin{aligned}A&={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}={\sqrt {16\cdot (16-4)\cdot (16-13)\cdot (16-15)}}\&={\sqrt {16\cdot 12\cdot 3\cdot 1}}={\sqrt {576}}=24.\end{aligned}}}
\begin{align}
A &= \sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)} = \sqrt{16 \cdot (16-4) \cdot (16-13) \cdot (16-15)}\
&= \sqrt{16 \cdot 12 \cdot 3 \cdot 1} = \sqrt{576} = 24.
\end{align}
In this example, the side lengths and area are integers, making it a Heronian triangle. However, Heron’s formula works equally well in cases where one or more of the side lengths are not integers.

2 Alternate expressions

Heron’s formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways,

{\displaystyle {\begin{aligned}A&={\tfrac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\[6mu]&={\tfrac {1}{4}}{\sqrt {2(a^{2}b{2}+a^{2}c{2}+b^{2}c{2})-(a^{4}+b{4}+c^{4})}}\[6mu]&={\tfrac {1}{4}}{\sqrt {(a^{2}+b{2}+c^{2}){2}-2(a^{4}+b{4}+c^{4})}}\[6mu]&={\tfrac {1}{4}}{\sqrt {4(a^{2}b{2}+a^{2}c{2}+b^{2}c{2})-(a^{2}+b{2}+c^{2}){2}}}\[6mu]&={\tfrac {1}{4}}{\sqrt {4a^{2}b{2}-(a^{2}+b{2}-c^{2}){2}}}.\end{aligned}}}{\displaystyle {\begin{aligned}A&={\tfrac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\[6mu]&={\tfrac {1}{4}}{\sqrt {2(a^{2}b{2}+a^{2}c{2}+b^{2}c{2})-(a^{4}+b{4}+c^{4})}}\[6mu]&={\tfrac {1}{4}}{\sqrt {(a^{2}+b{2}+c^{2}){2}-2(a^{4}+b{4}+c^{4})}}\[6mu]&={\tfrac {1}{4}}{\sqrt {4(a^{2}b{2}+a^{2}c{2}+b^{2}c{2})-(a^{2}+b{2}+c^{2}){2}}}\[6mu]&={\tfrac {1}{4}}{\sqrt {4a^{2}b{2}-(a^{2}+b{2}-c^{2}){2}}}.\end{aligned}}}
After expansion, the expression under the square root is a quadratic polynomial of the squared side lengths a2, b2, c2.

The same relation can be expressed using the Cayley–Menger determinant,

{\displaystyle -16A^{{2}={\begin{vmatrix}0&a}{2}&b^{2}&1\a{2}&0&c^{2}&1\b{2}&c^{2}&0&1\1&1&1&0\end{vmatrix}}.}{\displaystyle -16A^{{2}={\begin{vmatrix}0&a}{2}&b^{2}&1\a{2}&0&c^{2}&1\b{2}&c^{2}&0&1\1&1&1&0\end{vmatrix}}.}

3 History

4 Proofs

4.1 Trigonometric proof using the law of cosines

4.2 Algebraic proof using the Pythagorean theorem

4.3 Trigonometric proof using the law of cotangents

5 Numerical stability

6 Similar triangle-area formulae

7 Generalizations

7.1 Heron-type formula for the volume of a tetrahedron

7.2 Heron formulae in non-Euclidean geometries

8 See also