我们根据问题来引出邻接矩阵的各种含义：

目录

我们根据问题来引出邻接矩阵的各种含义：

1.如何计算指定顶点的度、入度、出度（分无向图、有向图来考虑)？时间复杂度如何?

2.如何找到与顶点相邻的边（入边、出边）？时间复杂度如何?

3.如何存储带权图?

4.空间复杂度―—O()，适合存储稠密图

5.无向图的邻接矩阵为对称矩阵，如何压缩存储?

6.设图G的邻接矩阵为A(矩阵元素为0/1），则An的元素An[i][i]等于由顶点i到顶点j的长度为n的路径的数目

---

1.如何计算指定顶点的度、入度、出度（分无向图、有向图来考虑)？时间复杂度如何?

（1）有向图

邻接矩阵中，值为0表示此值的横纵坐标所对应的两个结点之间没有边，反之则有边。

我们要横着看，在第一行中，只有一个1，也就表示结点A有一条指向结点B的边，A的出度加一，B的入度加一。

由此，我们通过观察邻接矩阵表可以知道，A指向B出度加1，C指向A入度加1,D指向A入度加1，结点A的度=入度+出度=2+1=3;

（2）无向图

邻接矩阵中，值为0表示此值的横纵坐标所对应的两个结点之间没有边，反之则有边。

由此，我们通过观察邻接矩阵表可以知道，结点A的度为3。(也就是第一行1的个数)

总度数=3+3+2+2+2+2=14

2.如何找到与顶点相邻的边（入边、出边）？时间复杂度如何?

如问题一的解答可以找到与顶点相邻的入边和出边个数，找出所有的边需要遍历每一个结点，所以它的时间复杂度为O(n);（n为结点个数）

3.如何存储带权图?

（1）无向图

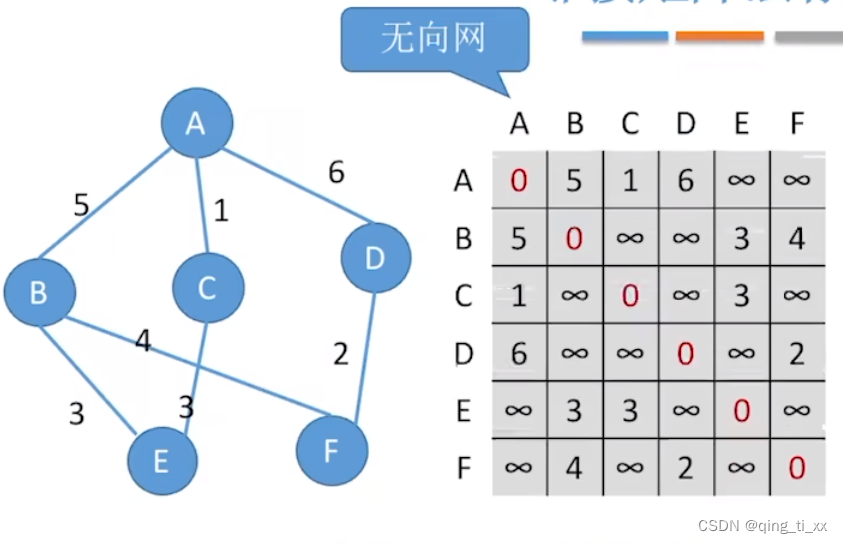
在无向图中，我们把每两个顶点之间的权值存入邻接表中，只要值不为0或∞，就表示这两者之间有边。

（2）有向图

与无向图类似，只要值不为0或∞，就表示这两者之间有边，只不过有向图表示的边具有指向性。

4.空间复杂度―—O()，适合存储稠密图

 就是一个二维数组的空间复杂度。

邻接矩阵存储的是结点之间的边，所以结点之间的边越多越好，所以适合存储稠密图。

5.无向图的邻接矩阵为对称矩阵，如何压缩存储?

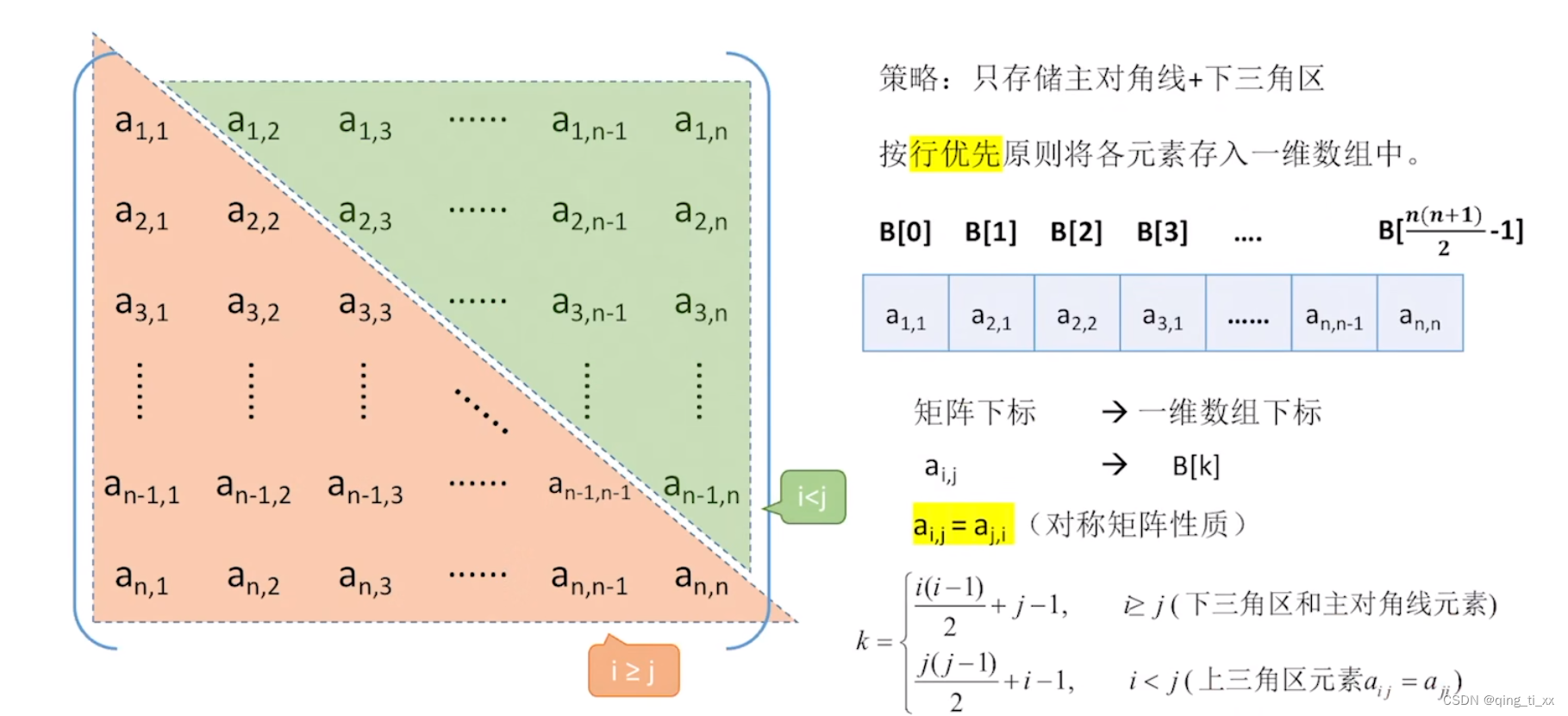
对称矩阵的上半三角和下半三角的值是一样的，如果使用二维数组就太浪费空间了，所以我们使用一维矩阵存储下半就行了。

6.设图G的邻接矩阵为A(矩阵元素为0/1），则An的元素An[i][i]等于由顶点i到顶点j的长度为n的路径的数目

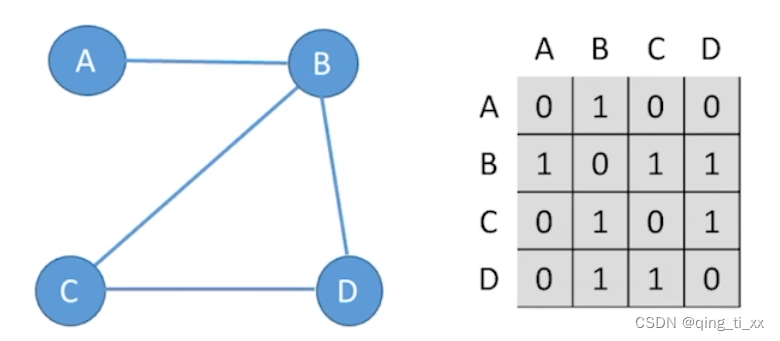
我们得到如上一个邻接矩阵，要我们算出某结点到某结点的长度为2路径有多少个，其实只需要对矩阵进行一次数乘就可以了

通过观察右边的矩阵，我们得知，从结点B到B的路径有3条，依此类推。

同理，如果想要计算某结点到某结点的长度为3路径有多少个，只需要算出矩阵.