本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你一个头结点为 head 的单链表和一个整数 k ，请你设计一个算法将链表分隔为 k 个连续的部分。

每部分的长度应该尽可能的相等：任意两部分的长度差距不能超过 1 。这可能会导致有些部分为 null 。

这 k 个部分应该按照在链表中出现的顺序排列，并且排在前面的部分的长度应该大于或等于排在后面的长度。

返回一个由上述 k 部分组成的数组。

示例 1：

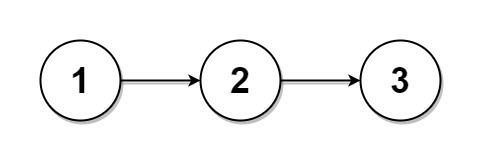
输入：head = [1,2,3], k = 5
输出：[[1],[2],[3],[],[]]
解释：
第一个元素 output[0] 为 output[0].val = 1 ，output[0].next = null 。
最后一个元素 output[4] 为 null ，但它作为 ListNode 的字符串表示是 [] 。

示例 2：

输入：head = [1,2,3,4,5,6,7,8,9,10], k = 3
输出：[[1,2,3,4],[5,6,7],[8,9,10]]
解释：
输入被分成了几个连续的部分，并且每部分的长度相差不超过 1 。前面部分的长度大于等于后面部分的长度。

提示：

• 链表中节点的数目在范围 [0, 1000]
• 0 <= Node.val <= 1000
• 1 <= k <= 50

---

解法 双重循环

题目要求将给定的链表分隔成 $k$ 个连续的部分。由于分隔成的每个部分的长度和原始链表的长度有关，因此需要首先遍历链表，得到链表的长度 $n$ 。

得到链表的长度 $n$ 之后，记 $\text{quotient}=\lfloor \frac{n}{k}\rfloor$ ，$\text{remainder}=n\mathrm{mod}k$ ，则在分隔成的 $k$ 个部分中，前 $remainder$ 个部分的长度各为 $quotient+1$ ，其余每个部分的长度各为 $\text{quotient}$ 。

分隔链表时，从链表的头结点开始遍历，记当前结点为 $curr$，对于每个部分，进行如下操作：

1. 将 $curr$ 作为当前部分的头结点；
2. 计算当前部分的长度 $partSize$；
3. 将 $curr$ 向后移动 $partSize$ 步，则 $curr$ 为当前部分的尾结点；
4. 当 $curr$ 到达当前部分的尾结点时，需要拆分 $curr$ 和后面一个结点之间的连接关系，在拆分之前需要存储 $curr$ 的后一个结点 $next$；
5. 令 $curr$ 的 $next$ 指针指向 $null$，完成 $curr$ 和 $next$ 的拆分；
6. 将 $next$ 赋值给 $curr$。

完成上述操作之后，即得到分隔链表后的一个部分。重复上述操作，直到分隔出 $k$ 个部分，或者链表遍历结束，即 $curr$ 指向 $null$ 。

class Solution {
public:
    vector<ListNode*> splitListToParts(ListNode* head, int k) {
        int n = 0;
        ListNode *temp = head;
        while (temp) { ++n; temp = temp->next; }
        int quotient = n / k, remainder = n % k;
        vector<ListNode*> parts(k, nullptr);
        ListNode* curr = head;
        for (int i = 0; i < k && curr; ++i) {
            parts[i] = curr;
            int partSize = quotient + (i < remainder ? 1 : 0);
            for (int j = 1; j < partSize; ++j) curr = curr->next;
            ListNode *next = curr->next;
            curr->next = nullptr;
            curr = next;
        }
        return parts;
    }
};

复杂度分析：

• 时间复杂度：$O(n)$ ，其中 $n$ 是链表的长度。需要遍历链表两次，得到链表的长度和分隔链表。
• 空间复杂度：$O(1)$ 。只使用了常量的额外空间，注意返回值不计入空间复杂度。