最近遇到一个开发问题，判断两个价格的大小，听着很简单，但其实价格是浮动的，也就是说价格是一个范围，比如物品A的价格是5～10，现在我们通过筛选条件，把价格符合在8～20之前的物品筛选出来，很明显物品A是符合这个筛选条件的，因为它的价格可以说8、9、10，完全符合在8～20的范围内。

此外，该问题还有一个条件，物品A的价格最小可以为0，最大可以为无限大，也就是当物品最大价格为10时，实际范围区间为无限小～10，当物品A最小价格为10时，实际范围区间为10～无限大；筛选条件也同时存在只有最大，只有最小，有最大有最小三种情况。

以上的问题，用代码如何实现呢？

如果按照平常的逻辑，我们需要两层嵌套，外层嵌套式判断筛选的价格情况，是只有最小，只有最大，或者有最小有最大，这三种情况，每一种情况里面又需要对物品的价格三种情况进行区分判断，又是一层嵌套，听着就很麻烦很绕，代码写起来也很冗余。

其实这个问题我们转换一下思路，筛选符合条件价格范围的物品，其实就是求两个区间的交集，回到了数学问题了，只有两个区间有交集，代表符合条件。

讲到区间与交集，要想到用线段来表示，如下图：

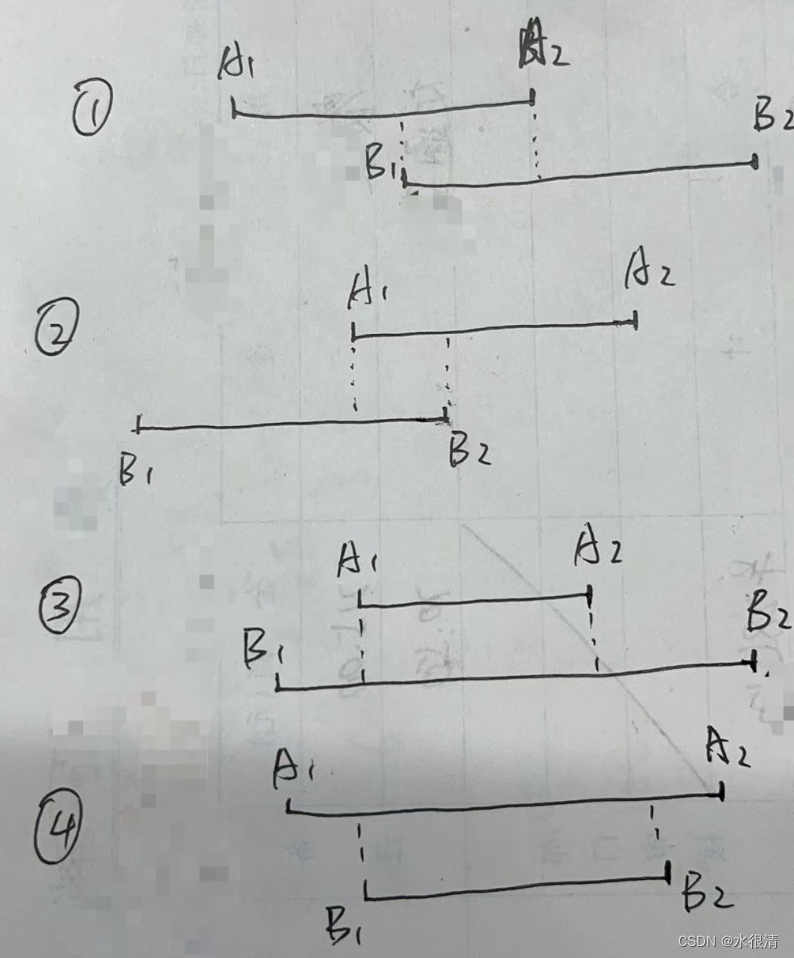
线段A1A2、B1B2之间存在交集有以上四种情况，交集的部分分别为以下四条线段

第一：B1A2

第二：A1B2

第三：B1A1

第四：A1B1

我们再来看，这四条线段的起点，也就是B1、A1、B1、A1是怎么得出来的

第一： B1 =  A1与B1 对比后取 其中的最大值

第二： A1 =  B1与A1 对比后取 其中的最大值

第三： B1 =  B1与A1 对比后取 其中的最大值

第三： A1 =  A1与B1 对比后取 其中的最大值

可以看到，起点都是两条线段的起点进行对比后取最大的那个作为起点，同理，交集的终点也是这个道理，只不过是取两条线段的终点进行对比后取最小的那个作为终点。

那么，在java中，我们就可以这么写

交集线段的起点：T1 = Math.max（A1,B1）

交集线段的终点：T2 = Math.min(A2，B2)

也就是说，当T1<T2的时候，就满足条件，因为数轴是从左到右数值递增的，T1>T2，说明终点反而是在起点的前面，这是完全不符合实际情况的，也说明T1>T2的情况是不存在交集的。

以上如果听明白了，那代码就好办了，很简单很简洁，调用以下方法即可以，其中前两个参数第一个区间的起点跟终点，第三第四个参数代表第二个区间的起点跟终点，方法返回true代表有交集符合条件，false则无交集不符合条件

private boolean judge(float a1, float a2, float b1, float b2) {
      if (a1 == 0 && a2 == 0) {
          return false;
      }
      return Math.max(a1, b1) <= Math.min(a2, b2);
}

if的判断，是排除掉，起点即是终点，是零点的情况。

that's all