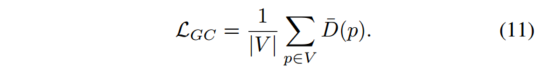2019 ICPC香港站 G. Game Design

news2025/1/10 11:33:03

Problem - G - Codeforces

问题描述：怪物只能在树叶子节点出生，向上走，可以花费一个值在一个节点建防御塔，防御塔会阻碍怪物向上走。最小花费可以让根节点无法被怪物走到的一个造塔方法算是一个方案。现给定方案数，让构造满足给定方案数的树。数据限制：节点数：[2, 1e5]，每一个防御塔的花费[1, 1e9]。

思路：可以发现对于一个合数，它可以分解成许多质因数，例如8，可以分解成2 2 2这三个2，那么树的构造就是：

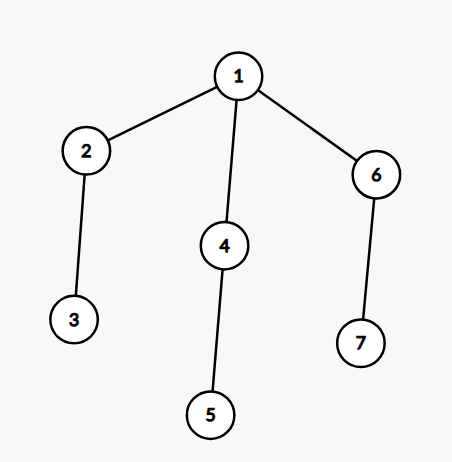
这个的方案数是：2 * 2 * 2。

如果是质数，例如11，可以进行减一操作后加上一个节点，在加的节点的基础上执行合数的操作方法。

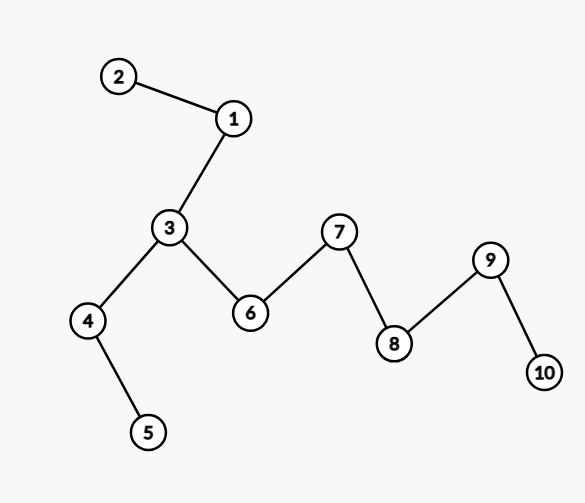
可以发现：是1 * 2(4-5) * 5(6-10) + 1(3-3) = 11，这个+1，是在节点3处。将节点2删除没有影响。

可以发现：每次进行操作，如果是质数就-1，加一个节点，在那个节点的基础上进行添加质数-1的所有最小质因子。如果是合数，就不额外添加节点，直接添加所有的最小质因子。

证明如下：常见的，1e5以内的质数个数不超过9.6e3，1e7以内的质数个数不超过6.7e6，1e9以内的质数不超过5.1e7。最坏的情况下，减完后进行分解存在大质数，那么仍需要进行减1再分解。存在相差为2的质数的情况在值很大的情况下很少，这个操作的时间复杂度是近似O(log(N))(考虑到质数之间的间隔等），同时，最多有log(N) * log(N)个节点数，及最多900个，但是实际情况远小于900，c的限制同理。

#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <queue>
#include <ctime>
#include <random>
#include <sstream>
#include <numeric>
#include <stdio.h>
#include <functional>
#include <bitset>
#include <algorithm>
using namespace std;

// #define Multiple_groups_of_examples
#define IOS std::cout.tie(0);std::cin.tie(0)->sync_with_stdio(false);
#define dbgnb(a) std::cout << #a << " = " << a << '\n';
#define dbgtt cout<<" !!!test!!! "<<endl;
#define rep(i,x,n) for(int i = x; i <= n; i++)

#define all(x) (x).begin(),(x).end()
#define pb push_back
#define vf first
#define vs second

typedef long long LL;
typedef pair<int,int> PII;

const int INF = 0x3f3f3f3f;
const int N = 2e5 + 21;

void inpfile();

// 试除法分解质因数
vector<int> divide(int x) {
    vector<int> res;
    for(int i = 2; i <= x / i; ++i) {
        if(x % i == 0) {
            while(x % i == 0) x /= i, res.push_back(i);
        }
    }
    if(x > 1) res.push_back(x);
    return res;
}
void solve() {
    int k; cin>>k;
    vector<int> fa(N),c(N); // fa --> i节点的父亲节点是哪个    c --> 第i个点的花销
    vector<vector<int>> g(N); // 建的图
    int cnt  = 1; // 树链的编号
    
    // 进行质数分解
    /**
     * 如果小于10，直接展开成链。
     * 如果大于等于10：
     *      进行质数分解：
     *          - 是质数，多加一个节点连接 (质数-1)的分解因子所成的链
     *          - 不是质数，将所有的最小的因子作为链首，并连接到所指向的父亲节点。
    */
    auto dfs1 = [&](auto &&dfs1, int now, int fu) -> void {
        if(now < 10) { // 小于10，将树链展开。
            int father = fu;
            for(int i = 1; i <= now; ++i) {
                fa[++cnt] = father; 
                g[father].push_back(cnt);
                father = cnt; // 父亲节点要一直更新
            }
            return ;
        }
        // 分解出所有的最小因数
        auto primes = divide(now);
        if(primes.size() == 1) { // 如果是质数，加一个节点，向下递归
            fa[++cnt] = fu;
            g[fu].push_back(cnt);
            dfs1(dfs1, now-1, cnt);
        } else { // 否则，将因数暂时指向当前父亲节点，进入递归去指向它真正的父亲节点
            for(auto t: primes) {
                // 因为当前t是因子，而因子可能很大，导致不满足这个条件：2 <= N <= 1e5，因此对于大于10的质数还要进行递归找最小的
                dfs1(dfs1, t, fu);
            }
        }
    };
    dfs1(dfs1, k, 1);
    cout<<cnt<<endl;

    // 自下向上找花费
    auto dfs2 = [&](auto&&dfs2, int u) -> void {
        if(g[u].size() == 0) {
            c[u] = 1;
            return ;
        }
        for(auto y: g[u]) {
            dfs2(dfs2,y);
            c[u] += c[y];
        }
    };
    dfs2(dfs2,1);
    for(int i = 2; i <= cnt; ++i) cout<<fa[i]<<" "; puts("");
    c[1] = 1e8; // 根节点不算
    for(int i = 1; i <= cnt; ++i) cout<<c[i]<<" ";
}
int main()
{
    #ifdef Multiple_groups_of_examples
    int T; cin>>T;
    while(T--)
    #endif
    solve();
    return 0;
}
void inpfile() {
    #define mytest
    #ifdef mytest
    freopen("ANSWER.txt", "w",stdout);
    #endif
}