Tensor 张量
Tensor,中文翻译“张量”,是一种特殊的数据结构,与数组和矩阵非常相似。在 PyTorch 中,使用张量对模型的输入和输出以及模型的参数进行编码。
Tensor 是一个 Python Class。PyTorch 官方文档中定义“Tensor,是一种包含单一数据类型元素的多维矩阵”。
官方:TORCH.TENSOR
A torch.Tensor is a multi-dimensional matrix containing elements of a single data type.
“张量” 看起来和矩阵比较相似,但实际上“张量” 和线性代数中的 “矩阵” 并不相同。
理解“张量”最简单的方法,是把它看成一个“多维数组”,这个数组可以是 0 维,即一个数值(称为“标量”);也可以是 1 维,即一个常见的普通数组(称为“矢量/向量”);还可以是 2 维、3维、甚至 N 维;
一维
import torch
# 一维
a = torch.tensor([1, 2, 3, 4])
print(a) # tensor([1, 2, 3, 4])
print(a.shape) # torch.Size([4])
# 输出只有一个维度,所以是一维。二维
import torch
# 二维
a = torch.tensor([[1, 2, 3, 4]])
print(a) # tensor([[1, 2, 3, 4]])
print(a.shape) # torch.Size([1, 4])上面输出有行和列,所以它二维张量,实际上就是一个二维矩阵。
三维
import torch
# 三维
a = torch.ones(1, 3, 3)
print(a)
print(a.shape)打印结果:
tensor([[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]])
torch.Size([1, 3, 3])从输出结果可以看到这个张量是有三个维度的,前面多了一个维度1。但无法直观看到这个1体现在哪里。下面再来看一个张量,直观感受一下这个最前面的维度体现在哪里:
import torch
# 三维
a = torch.ones(3,4,5)
print(a)
print(a.shape)打印结果:
tensor([[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]]])
torch.Size([3, 4, 5])
从上面输出结果,可以直观感受到最前面维度(数字3)的体现;
第一个数字3:分成3大行
第二个数字4:每一大行分为4小行
第三个数字5:每一大行分为5小列
所以数据的维度是3×4×5,最后一个数字表示列的维度;我们也可以理解为3个4行5列的数据。
如果我们将上面的张量类比为一张RGB的图像,数字3表示3个通道,每个通道的大小为4行5列。
四维
import torch
# 四维
a = torch.ones(2,3,4,5)
print(a)
print(a.shape)打印结果:
tensor([[[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]]],
[[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]],
[[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]]]])
torch.Size([2, 3, 4, 5])
我们用分割线将上面的输出分开:
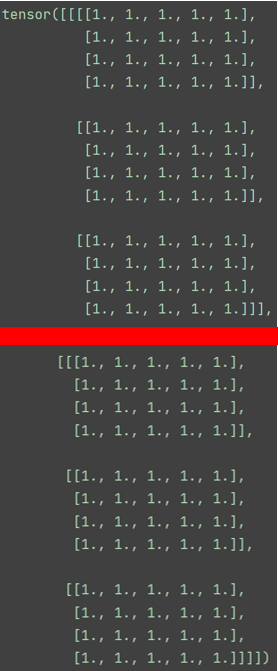
红线上面一部分是一个“维度”,下面又是一个“维度”,所以是两个维度。
再直白一点,就是张量a,有2大行,每大行又分了3小行,每行又分了4行,然后又分了5列。
张量a在日常图像数据集中可以这么理解:
第一个数字2:其实就是batch_size,就相当于这个张量是输入了2张图像
第二个数字3:每张图像的通道数是3
第三个数字4:图像的高为4
第四个数字5:图像的宽为5
如下所示:
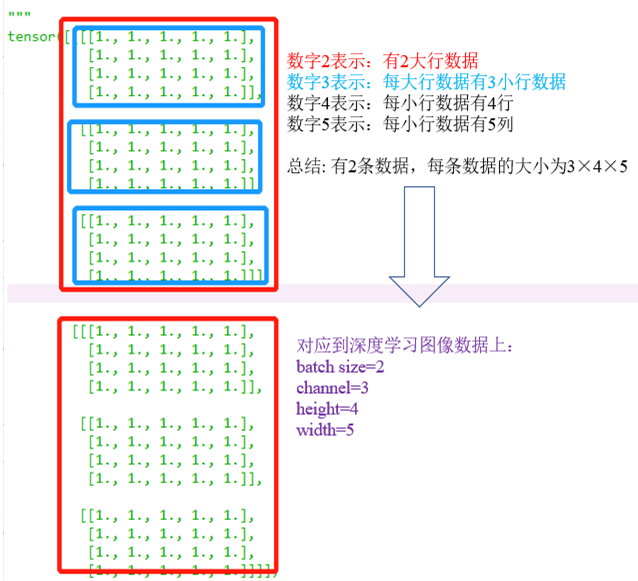
N维数组的角度理解彩色图像
下面这个示例,更直观的描绘了如何从 “ N 维数组 ” 的角度,理解一张彩色图片:
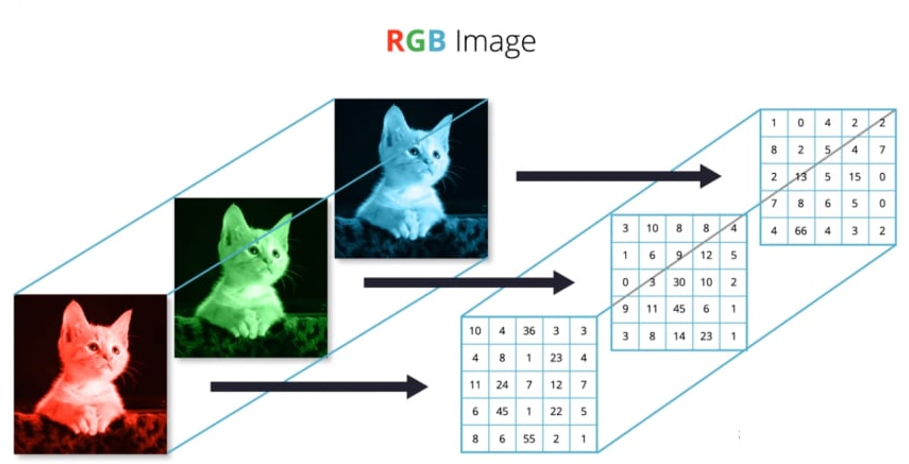
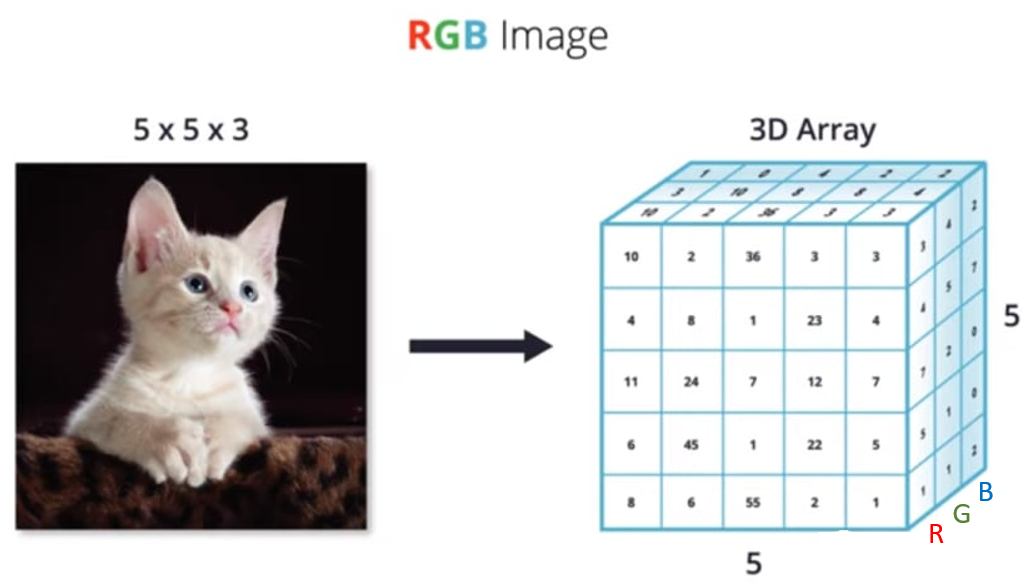
现实世界中的数据张量
向量数组(2D 张量)
这是最常见的数据。它是由向量组成的数组,第一个轴是样本轴,第二个轴是特征轴。
案例
-
人口统计数据集,包括三个特征:年龄、电话和收入。因此可以存储在形状为 (x, 3) 的 2D 张量中,x 为统计人数。
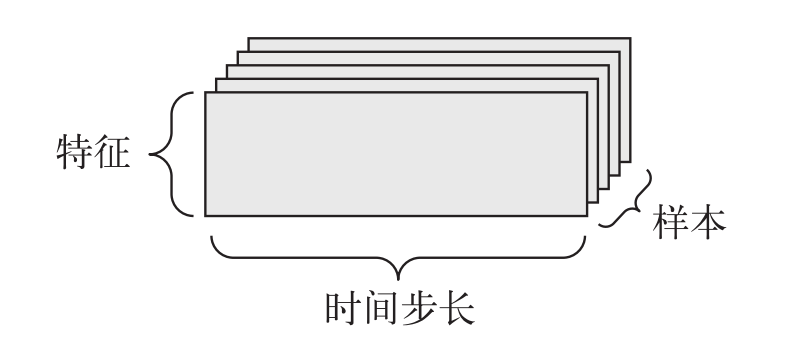
时间序列数据(3D 张量)
当数据集中时间(或序列顺序)对于数据很重要时,应该将数据存储在带有时间轴的 3D 张量中。每个样本可以被编码为一个向量序列(即 2D 张量),而一个数据批量就是一个 3D 张量。
案例
-
股票价格数据集。每一分钟,我们记录股票的当前价格、上一分钟的最高价格和上一分钟的最低价格。整个交易日保存在形状为 (x, 3) 的 2D 张量(x 统计时长)中,而 300 天的数据则可以保存在形状为(300, x, 3)的 3D 张量中。这里每个样本是一天的股票数据。
批图像数据(4D 张量)
PIL image张量格式一般都是(W,H,C),而PyTorch的图像张量一般格式是(C,H,W)(C为通道数,H为高,W为宽),所以需要把它转换为PyTorch里面的张量形式。即有变换(W,H,C)-->(C,H,W)。
方法:采用transforms.ToTensor()方法。
图像通常具有三个维度:高度、宽度和颜色深度。虽然灰度图像(比如 MNIST 数字图像) 只有一个颜色通道,因此可以保存在 2D 张量中。
如果图像大小为 256×256,
-
128 张灰度图像组成的批量可以保存在一个形状为(128, 1, 256, 256 )的张量中;
-
128 张彩色图像组成的批量则可以保存在一个形状为(128, 3, 256, 256)的张量中。
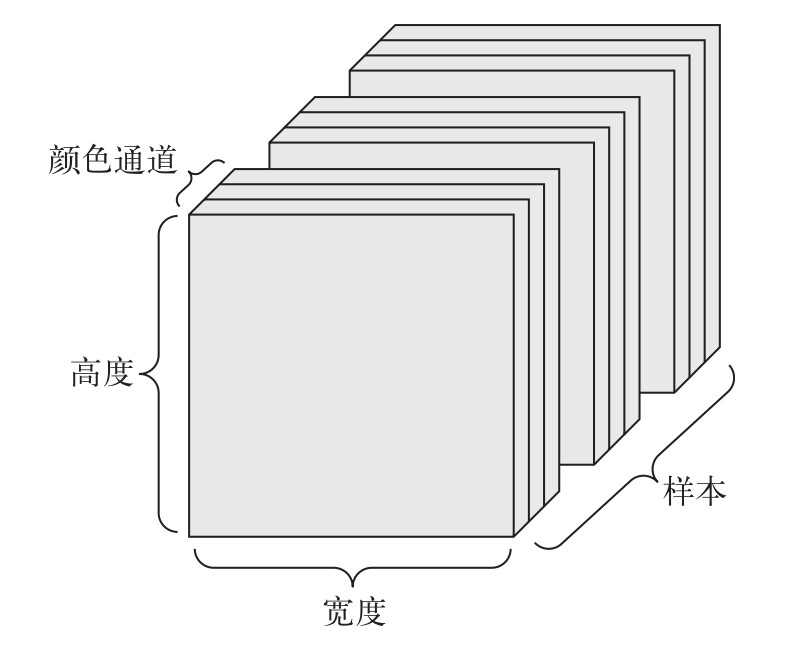
4 维张量在卷积神经网络中应用的非常广泛,它用于保存特征图(Feature maps)数据,格式一般定义为:(PyTorch版本)
[b,c,h,w]
其中𝑏表示输入的数量(批次大小batch_size),h/w分别表示特征图的高宽,𝑐表示特征图的通道数。
图片数据是特征图的一种,对于含有RGB 3 个通道的彩色图片,每张图片包含了h 行w 列像素点,每个点需要3 个数值表示RGB 通道的颜色强度,因此一张图片可以表示为[3, h, w]。如下图所示,最上层的图片表示原图,它包含了下面3 个通道的强度信息。

神经网络中一般并行计算多个输入以提高计算效率,故 𝑏 张图片的张量可表示为 : [b,c,h,w]
对于4维张量的索引
张量的索引是从第零维度开始的。让我们来创建一个四维的张量做举例说明:torch.Tensor(2,3,52,64) 此时,这个张量可以表示两张高为52宽为64的彩色图像,具体来说,张量的第零维表示图像的数量;第一维表示图像的颜色通道(3即为彩色图片,代表RGB三通道);第二维和第三维代表图像的高度和宽度。此张量的索引代码如下:
import torch
a = torch.Tensor(2, 3, 52, 64)
# 通过.shape的方法查看当前张量的形状
print(a.shape)
print(a[0].shape)
print(a[0][0].shape)
print(a[0][0][0].shape)
print(a[0][0][0][0].shape)打印结果:
torch.Size([2, 3, 52, 64]) # 图像的形状
torch.Size([3, 52, 64]) # 取到第一张图像,形状为 [3, 52, 64]
torch.Size([52, 64]) # 取到第一张图像的第一个颜色通道, 形状为[52, 64]
torch.Size([64]) # 取到第一张图像的第一个颜色通道的第一行像素值
torch.Size([]) # 取到第一张图像的第一个颜色通道的第一个像素值,形状为0(因为是标量)
对于四维张量的切片问题
在上一小节中,维度的索引是取到某维度上的全部数据。但是,如果我们只想要某维度上的部分数据应该怎么做呢?这就是切片的作用。
切片方法的格式为:tensor[ first : last : step] ,first与last为切片的起始和结束位置,取值方法是按照step的间隔进行左闭右开的取值;当间隔为1时,step可以默认不写;当取到该维度的所有数据时,使用冒号即可。实例如下:
import torch
a = torch.Tensor(2, 3, 64, 64)
# 通过.shape的方法查看当前张量的形状
print(a.shape)
print(a[1:2, :, :, :].shape)
print(a[ : , : , 0:32, 0:32].shape)
print(a[ : , : , 0:32:2, 0:32:2].shape)
print(a[ : , : , : : 2, : : 2].shape)
打印结果:
torch.Size([2, 3, 64, 64]) # 图像的形状
torch.Size([1, 3, 64, 64]) # 取到第二张图像
torch.Size([2, 3, 32, 32]) # 取到两张图像1/4大小的左上角子图
torch.Size([2, 3, 16, 16]) # 取到两张图像1/4大小的左上角子图后,在子图上隔点取样
torch.Size([2, 3, 32, 32]) # 在原图上隔点取样
张量的维度变换
在之后的学习中我们会发现每个算法模型都有自己要求的输入数据维度,每个问题下的数据维度也不同。因为,为了使用各种的算法来处理各种的问题往往需要对数据进行维度的变换。例如,如果想用神经网络层来处理图像数据,我们就可以发现,图片是三维的数据维度(颜色通道,高度,宽度),但是神经网络层能接受的数据维度是二维,此时维度是不匹配的,因此需要将图像的空间维度打平成向量。下面介绍pytorch中一些常见的维度变换方法。
(1) view() 和 reshape() 变换维度
import torch
a = torch.Tensor(2, 3, 32, 32)
print(a.view(2, 3, 32*32))
print(a.reshape(2, 3, 32*32))
print(a.reshape(2, 3, -1))
print(a.view(2, 3, 32 * 32).shape)
print(a.reshape(2, 3, 32 * 32).shape)
print(a.reshape(2, 3, -1).shape)打印结果:
tensor([[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]],
[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]])
tensor([[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]],
[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]])
tensor([[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]],
[[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]])
torch.Size([2, 3, 1024])
torch.Size([2, 3, 1024])
torch.Size([2, 3, 1024])
view() 和reshape()都可以对某张量进行维度的变化,但是reshape()方法的鲁棒性更强,更推荐大家使用。此外,view() 和reshape()接受的参数都是变换后的维度大小,在设置变换后维度的参数时,如果只剩一个维度没有给予,可直接使用-1来代替,pytorch会根据之前已设置的维度自动推导出最后未给予的维度。
import torch
a = torch.Tensor(2, 3, 32, 32)
print(a.reshape(2, 3, 4,-1).shape) # 打印结果:torch.Size([2, 3, 4, 256])
最后,这里需要注意的是变换后的总维度数量必须与变换前相等,否则报错。实例如下所示:
import torch
a = torch.Tensor(2, 3, 32, 32)
print(a.reshape(2, 3, 10).shape)
# RuntimeError: shape '[2, 3, 10]' is invalid for input of size 6144(2) unsqueeze() 增加新的数据维度
有时候,我们往往因为数据的增加需要在原始张量表示的基础上扩张维度来存储新增加的数据。举个例子,我们创建一个小学年级的档案时,可以创建一个三维张量:[年级数量,每年级的班级数量,班级的人数] ,此时,我要合并另一所学校的年级档案,最好的办法是在扩充出一个学校的维度,变成四维张量:[学校的数量,年级数量,每年级的班级数量,班级的人数] 。 unsqueeze() 方法就是用来增加数据维度的,接受的参数含义是在哪个维度之前增加新维度,这个参数也支持负索引。具体实例如下:
import torch
a = torch.Tensor(2, 3, 64, 64)
print(a.unsqueeze(0).shape)
print(a.unsqueeze(1).shape)
print(a.unsqueeze(2).shape)
print(a.unsqueeze(-1).shape)
# output
# torch.Size([1, 2, 3, 64, 64])
# torch.Size([2, 1, 3, 64, 64])
# torch.Size([2, 3, 1, 64, 64])
# torch.Size([2, 3, 64, 64, 1])(3) squeeze() 缩减数据维度
增加某张量维度的反操作是减少维度,对于pytorch中的方法是squeeze(),接受的参数是要进行维度缩减的维度索引,注意,缩减的维度值必须等于1,否则不能进行缩减,而且程序不报错,实例如下:
import torch
a = torch.Tensor(2, 1, 64, 64)
print(a.squeeze(1).shape)
print(a.squeeze(2).shape)
# output
# torch.Size([2, 64, 64])
# torch.Size([2, 1, 64, 64])
(4) expand()和 repeat()在某维度上扩展数据
expand()可以在某维度上进行数据扩展,扩展的方法是复制原始数据。需要注意的是,expand()方法不能扩展维度大于1的维度,否则报错。因为其扩展方式是复制,当维度大于1时,expand()方法不清楚应该复制哪个数据。具体实例如下:
import torch
a = torch.Tensor(2, 1, 64, 64)
print(a.shape)
print(a.expand(2, 3, 64, 64).shape)
print(a.expand(2, 100, 64, 64).shape)
# torch.Size([2, 1, 64, 64])
# torch.Size([2, 3, 64, 64])
# torch.Size([2, 100, 64, 64])
print(a.expand(3, 1, 64, 64).shape)
# RuntimeError: The expanded size of the tensor (3) must match the existing size (2) at non-singleton dimension 0. Target sizes: [3, 1, 64, 64]. Tensor sizes: [2, 1, 64, 64]
repeat()也可以在某维度上进行数据扩展,但是其接受的参数含义与expand()函数不同。repeat()函数接受的是在该维度上复制全部数据的次数,实例如下:
import torch
a = torch.Tensor(2, 1, 64, 64)
print(a.shape)
print(a.repeat(1,3,1,1).shape)
print(a.repeat(3,3,3,3).shape)
# output
# torch.Size([2, 1, 64, 64])
# torch.Size([2, 3, 64, 64])
# torch.Size([6, 3, 192, 192])
(5) transpose()和 permute()进行张量的维度调整
transpose()可以通过指定张量中某两个维度的索引,来对这两个维度的数据进行交换维度操作,示例如下:
import torch
a = torch.Tensor(2, 3, 64, 64)
print(a.shape)
print(a.transpose(0, 1).shape)
# output
# torch.Size([2, 3, 64, 64])
# torch.Size([3, 2, 64, 64])
(6) Broadcast:pytorch对不同维度张量进行计算时的自动补全规则
注意,broadcast不是函数,而是pytorch在加减两个不同维度张量时,底层自动实现的计算逻辑。首先,一个常识是当两个张量维度不同时,是不能进行加减操作的。broadcast的主要思想是针对维度小的数据依次从最后一个维度开始匹配维度大的数据,如果没匹配上,则插入一个新的维度。举例如下:
[2, 3, 32, 32] + [3,1,1] 是不能直接相加的。
Broadcast机制会先将 [3,1,1] 增加新维度变为 [1, 3, 1, 1] (等价于unsqueeze()方法),然后再将 [1, 3, 1, 1]扩展维度为 [2, 3, 32, 32] (等价于expand()方法)
从某种程度上说,broadcast机制等价于unsqueeze()和expand()两个方法的组合。目的是在处理两个维度不同的张量时,可以显式的不做任何处理进行直接加减操作。实际上,在底层隐式的进行了unsqueeze() 和 expand()。
注意,broadcast机制也有限制:当维度小的数据依次从最后一个维度开始匹配维度大的数据时,小维度数据的维度值必须符合以下两种情况之一,才能进行broadcast:等于1或与大维度数据的维度值相等,否则报错。示例如下:
import torch
a = torch.Tensor(2,3,32,32)
b = torch.Tensor(1,1,1)
c = torch.Tensor(32)
d = torch.Tensor(32, 1)
e = torch.Tensor(2, 32, 32)
print((a + b).shape) # 运行成功
print((a + c).shape) # 运行成功
print((a + d).shape) # 运行成功
print((a + e) .shape) # 报错
# torch.Size([2, 3, 32, 32])
# torch.Size([2, 3, 32, 32])
# torch.Size([2, 3, 32, 32])
# RuntimeError: The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1import torch
a = torch.Tensor(2, 3, 32, 32)
d = torch.Tensor(2, 32, 32)
e = torch.Tensor(1, 32, 32)
print((a + e) .shape) # 运行成功
print((a + d).shape) # 报错
# torch.Size([2, 3, 32, 32])
# RuntimeError: The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1
参考自:
微信公众号 Python新视野 10分钟看懂深度学习的基本数据类型——张量
微信公众号 板栗烧鸡翅【PyTorch笔记】基础知识:Tensor 张量
https://blog.csdn.net/python_LC_nohtyp/article/details/104097182
【DL】关于tensor(张量)的介绍和理解_机器不学习我学习的博客-CSDN博客
【Pytorch基础(2)】张量的索引,切片与维度变换_python 张量索引_lingchen1906的博客-CSDN博客