步骤：
1、 编程 将PPT 的例子 跑一遍， 确保代码无误
2、根据题目 修改 相关参数

解决的问题： 线段间转折点 的 速度 不连续
解决方法： 将直线段 两端 修正为 二次方程式

二次项圆滑

求解代码_Python

import numpy as np
np.set_printoptions(precision=2,suppress = True) 

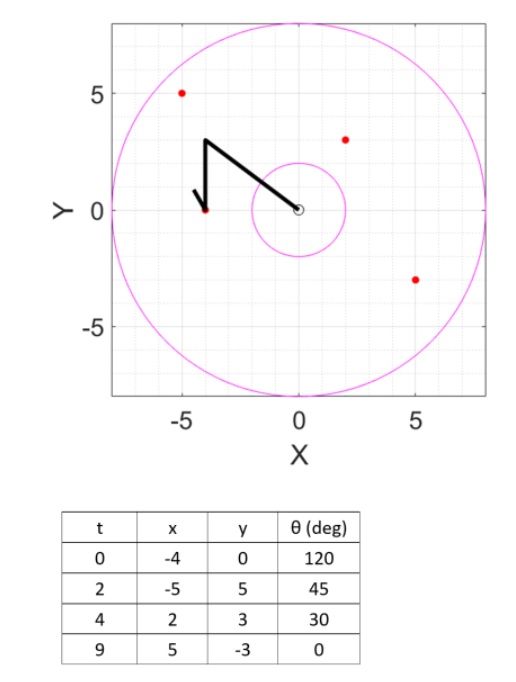
t0, t1, t2, tf = 0, 2, 4, 9
x0, x1, x2, xf = -4, -5, 2, 5
y0, y1, y2, yf = 0, 5, 3, -3 
θ0, θ1, θ2, θf = 120, 45, 30, 0
tk = 0.5

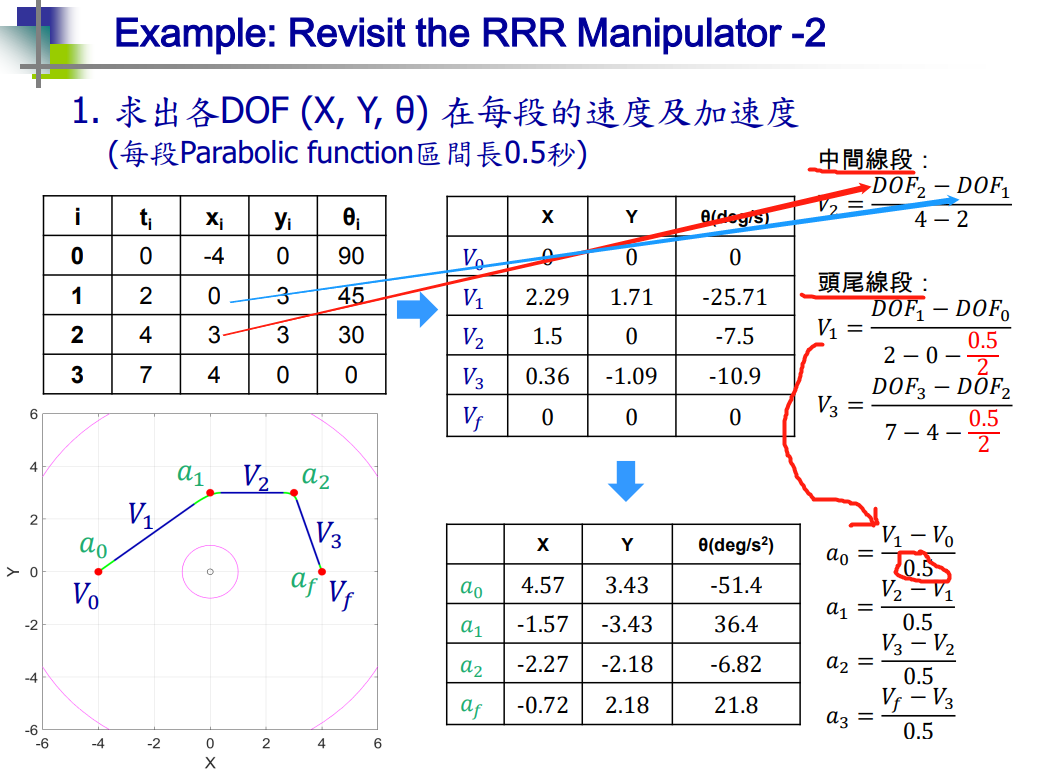
### 1、求 各 DOF(X, Y, θ) 在每段的速度  及 加速度

## 中间 线段 计算
def getV_in(x1, x2, t1, t2):
    return (x2 - x1)/(t2 - t1)

## 头尾 线段  计算 
def getV_0f(x1, x2, t1, t2):
    return (x2 - x1)/(t2 - t1 - tk/2)

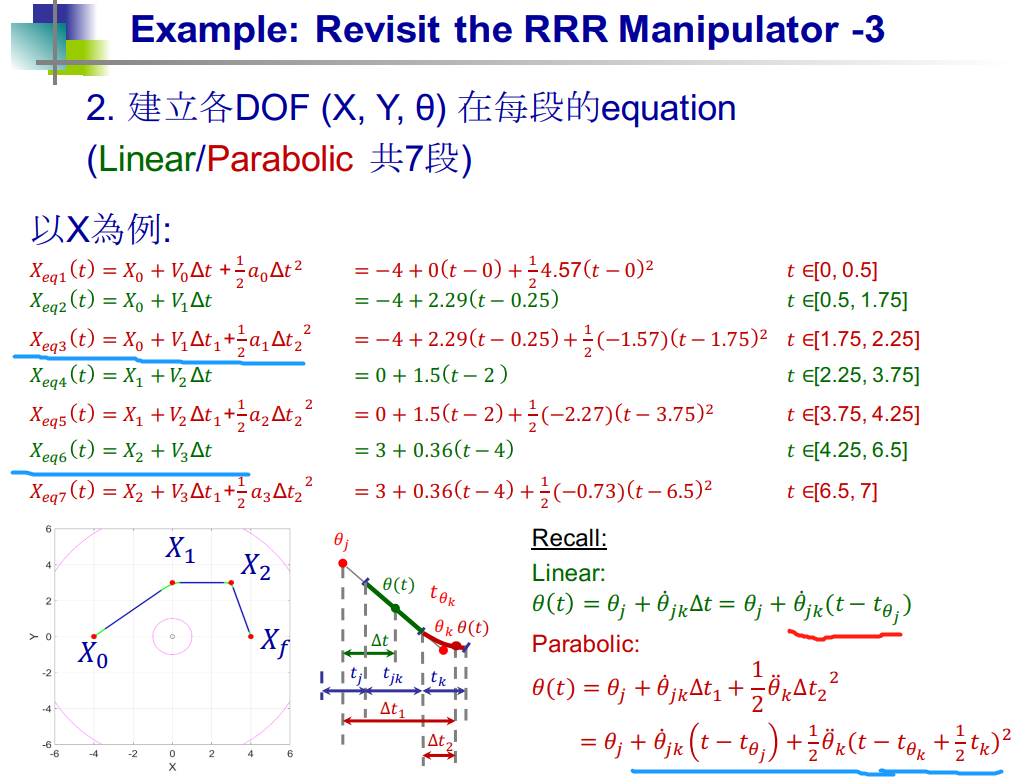
### 2、 建立 各 DOF(X, Y, θ) 在每段的方程
"""
平滑  t ∈ [0, 0.5]
直线  t ∈ [0.5, 1.75]
平滑  t ∈ [1.75, 2.25]
直线  t ∈ [2.25, 3.75]
平滑  t ∈ [3.75, 4.25]
直线  t ∈ [4,25, 8.5]
平滑  t ∈ [8.5, 9]
"""
## 求解 X(t)
##  平滑化  段  
def getX_parabolic(x, V, a, ti0, ti1, t):
    return x + V * (t - ti0) + 0.5 * a * (t - ti1)**2

## 直线段  
def getX_linear(x, V, ti, t):
    return x + V * (t - ti)


############# 求解 X 部分
print('X:')
V0 = 0
V1 = getV_0f(x0, x1, t0, t1)
V2 = getV_in(x1, x2, t1, t2)
V3 = getV_0f(x2, xf, t2, tf)
Vf = 0
print('V1[0.5 ~ 1.75]:', np.round(V1, 2))
print('V2[2.25 ~ 3.75]:', np.round(V2, 2))
print('V3[4.25 ~ 8.25]:', np.round(V3, 2))  


def geta(V1, V2):
    return (V2 - V1)/tk

a0 = geta(V0, V1)
a1 = geta(V1, V2)
a2 = geta(V2, V3)
af = geta(V3, Vf)
print('a0:', np.round(a0, 2))
print('a1:', np.round(a1, 2))
print('a2:', np.round(a2, 2))
print('af:', np.round(af, 2))

print('t ∈ [3.75, 4.25]  t = 4 , X5 = :', np.round(getX_parabolic(x1, V2, a2, 2, 3.75, 4), 2))

############# 求解 Y 部分
print('Y:')
V0 = 0
V1 = getV_0f(y0, y1, t0, t1)
V2 = getV_in(y1, y2, t1, t2)
V3 = getV_0f(y2, yf, t2, tf)
Vf = 0
print('V1:', np.round(V1, 2))
print('V2:', np.round(V2, 2))
print('V3:', np.round(V3, 2))  


def geta(V1, V2):
    return (V2 - V1)/tk

a0 = geta(V0, V1)
a1 = geta(V1, V2)
a2 = geta(V2, V3)
af = geta(V3, Vf)
print('a0:', np.round(a0, 2))
print('a1:', np.round(a1, 2))
print('a2:', np.round(a2, 2))
print('af:', np.round(af, 2))

print('t ∈ [3.75, 4.25]  t = 4 , Y5 = :', np.round(getX_parabolic(y1, V2, a2, 2, 3.75, 4), 2))

############# 求解 θ 部分
print('θ:')
V0 = 0
V1 = getV_0f(θ0, θ1, t0, t1)
V2 = getV_in(θ1, θ2, t1, t2)
V3 = getV_0f(θ2, θf, t2, tf)
Vf = 0
print('V1:', np.round(V1, 2))
print('V2:', np.round(V2, 2))
print('V3:', np.round(V3, 2))  


def geta(V1, V2):
    return (V2 - V1)/tk

a0 = geta(V0, V1)
a1 = geta(V1, V2)
a2 = geta(V2, V3)
af = geta(V3, Vf)
print('a0:', np.round(a0, 2))
print('a1:', np.round(a1, 2))
print('a2:', np.round(a2, 2))
print('af:', np.round(af, 2))

print('t ∈ [3.75, 4.25]  t = 4 , θ5 = :', np.round(getX_parabolic(θ1, V2, a2, 2, 3.75, 4), 2))

第1题答案： -0.57//2.86//-42.86

第2题答案： 3.5//-1//-7.5

第3题答案： 0.63//-1.26//-6.32

第4题答案： -1.14//5.71//-85.71

第5题答案： 8.14//-7.71//70.71

第6题答案： -5.74//-0.53//2.37

第7题答案： -1.26//2.53//12.63

第8题答案： 1.82//2.98//30.07