根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

思路

---

首先知道怎么画，然后写代码流程。

以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

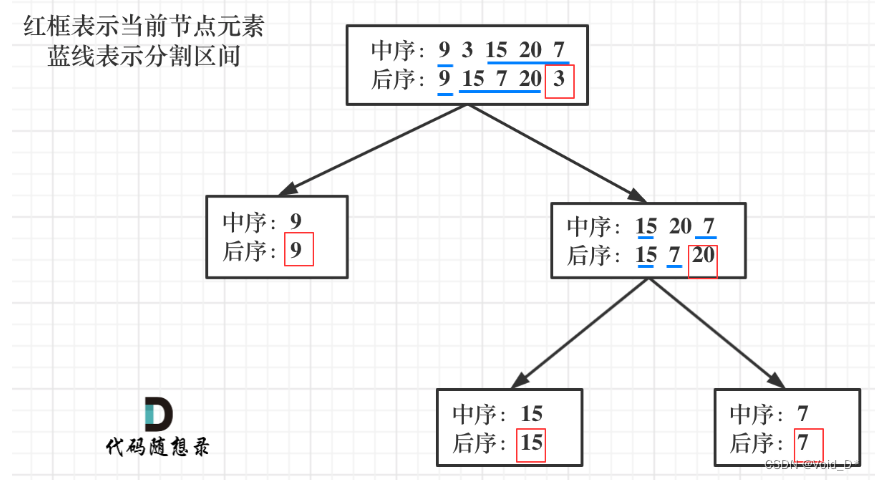
需要层层切割，获得节点，可以考虑递归。

来看一下一共分几步：

• 第一步：如果数组大小为零的话，说明是空节点了。

• 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

• 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）

• 第五步：切割后序数组，切成后序左数组和后序右数组

• 第六步：递归处理左区间和右区间

代码框架如下：

class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(postorder.size() == 0) return NULL;

        int rootVal = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootVal);

        if(postorder.size() == 1) return root;
        //第三步 找切割点
        int delimiterIndex;
        for(delimiterIndex=0;delimiterIndex < inorder.size();delimiterIndex++){
            if(inorder[delimiterIndex] == rootVal) break;
        }

        //第六步 继续构建
        root->left = buildTree();
        root->right = buildTree();
    }
};

如何准确切割中序和后序数组，找对边界值。

在切割过程中会出现四个区间，要保证区间表示全程不变性。

先根据后序数组的最后一个元素来切割中序数组。

然后根据中序数组的前后部分长度来切割后序数组。（因为中序和后序切割部分前后长度一致）

• 先切割中序部分：

//中序切割部分  左闭右开区间
        vector<int> leftInorder(inorder.begin(), inorder.begin()+delimiterIndex);
        vector<int> rightInorder(inorder.begin()+delimiterIndex+1, inorder.end());

• 切割后序部分

//后序部分
        postorder.resize(postorder.size()-1);
        vector<int> leftPostorder(postorder.begin(), postorder.begin()+leftInorder.size());
        vector<int> rightPostorder(postorder.begin()+leftInorder.size(), postorder.end());

完整代码：

class Solution {
public:
    TreeNode* traversal(vector<int>& inorder, vector<int>& postorder)
    {
        if(postorder.size() == 0) return NULL;

        int rootVal = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootVal);

        if(postorder.size() == 1) return root;
        //第三步 找切割点
        int delimiterIndex;
        for(delimiterIndex=0;delimiterIndex < inorder.size();delimiterIndex++){
            if(inorder[delimiterIndex] == rootVal) break;
        }
        //中序切割部分  左闭右开区间
        vector<int> leftInorder(inorder.begin(), inorder.begin()+delimiterIndex);
        vector<int> rightInorder(inorder.begin()+delimiterIndex+1, inorder.end());
        //后序部分
        postorder.resize(postorder.size()-1);
        vector<int> leftPostorder(postorder.begin(), postorder.begin()+leftInorder.size());
        vector<int> rightPostorder(postorder.begin()+leftInorder.size(), postorder.end());

        //第六步 继续构建
        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);

        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};

下面用索引下标，省去vector.

class Solution {
private:
    // 中序区间：[inorderBegin, inorderEnd)，后序区间[postorderBegin, postorderEnd)
    TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
        if (postorderBegin == postorderEnd) return NULL;

        int rootValue = postorder[postorderEnd - 1];
        TreeNode* root = new TreeNode(rootValue);

        if (postorderEnd - postorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割后序数组
        // 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)
        int leftPostorderBegin =  postorderBegin;
        int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
        // 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)
        int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
        int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        // 左闭右开的原则
        return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};