目录

1.第k个数

2. 多米诺骨牌

 3.构造序列

---

 

1.第k个数

题目描述

给定一个长度为n的整数序列，a1,a2,...,an,以及一个整数k，请你计算该数列从大到小排序后的第k个数。

输入格式

第一行包含两个整数n，k

第二行n个整数 

输出格式

输出一个数，表示答案 

数据范围

1<=n<=1000

1<=k<=n

0<=a[i]<=100 

样例输入 1：

5 3

20 10 30 40 10

样例输:1：

20

样例输入2：

6 5

90 20 35 40 60 100

样例输出2：

35

 样例输入3：

4 3

4 3 3 2

样例输出3：

3

我们可以从小到大排序，如何输出第n-k个数即可。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=1e6+10;
int a[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1);
    cout<<a[n-k];
    return 0;
}

2. 多米诺骨牌

题目描述

将n块多米诺骨牌排成一排，每块骨牌垂直竖立。

开始时，同时将一些骨牌推倒，有的向右倒，有的向左倒。

保证这些开始就被退倒的骨牌中，任意两块倒向同一方向的骨牌之间都至少存在一块倒向反方向的骨牌。

每一秒后，每个向左倒的骨牌都会推倒其左侧相邻的骨牌，每个向右侧倒的骨牌 都会推倒向右侧相邻的骨牌。

如果在某一时刻，某骨牌两侧的相邻骨牌同时推倒它，则由于力的平衡，则该骨牌会保持竖直不变。

下图给出了几种情况

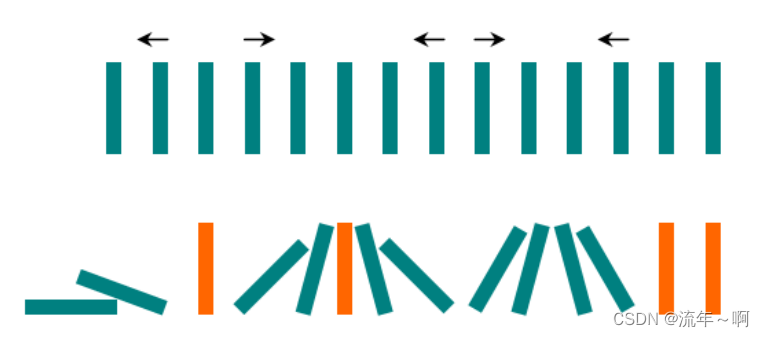
给定每块骨牌的初始状态，请你判断推倒完毕后，有多少骨牌仍然保持竖直。

输入格式

第一行一个整数n。

第二行包含一个长度为n的字符串，其中的第i个字符表示第i个字符的初始状态：

L表示该骨牌初始时向左倒。

R表示该骨牌初始时向右倒。

保证对于(i,j):

如果i<j,且si和sj均为L,则一定存在k满足i<k<j且sk为R;

如果i<j，且si和sj均为R，则一定存在k满足i<k<j且sk为L; 

 输出格式

一个整数，表示最终保持垂直竖立骨牌的数量。

数据范围

1<=n<=3000 

样例输入1：

14

.L.R...LR..L..

样例输出：

4 

样例输入2：

5

R....

样例输出2：

0

样例输入3：

1

.

样例输出3：

1

思路：如果刚开始的位置存在L,则下一个要推倒的姿态是R，也就是R和L相互间隔。

不会被推倒的骨牌分下面三种情况：

1.如果刚开始存在R,则它前面的都不会被推倒，同理，如果最后一个被推倒的姿态是L，那么它后面的也不会被推倒，还有一种特殊情况，如果没有被推倒的状态，结果为n；

2.如果骨牌在L和R之间，则不会被推倒。

3.如果骨牌在R和L之间，如果骨牌数为奇数，至少存在一个不会被推倒，如果是偶数，则全部都会被推倒。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;

int main()
{
    int n;
    string str;
    cin>>n>>str;
    
    int l=0;
    while(l<n&&str[l]=='.') l++;//第一种情况左边没有被推倒的数
    
    int res=0;
    if(l==n) res=n;//如果不存在被推倒的状态，那么全部都是没有被推倒
    else
    {
        if(str[l]=='R') res=l;//左边存在的数
        int r=n-1;
        while(str[r]=='.') r--;
        if(str[r]=='L') res+=n-1-r;//右边存在的
        
        for(int i=l+1,cnt=0;i<=r;i++)
        {
            if(str[i]=='.') cnt++;
            else
            {
                if(str[i]=='L') res+=cnt%2;//第三种情况
                else res+=cnt;//第二种情况
                cnt=0;
            }
        }
    }
    cout<<res;
    return 0;
}

 3.构造序列

题目描述

请你构造一个01序列，序列满足：

恰好有n个0和m个1.不存在两个或两个以上的0连续相邻，不存在三个或者三个以上的1相邻

如果不存在，输出-1；

思路：我们可以先讨论0，不存在两个以上的0相邻，那么至少需要n-1个1，不存在3个以上的1，我们先把两个1放在一起，那么一共有m/2个1，那么至少存在(m/2)-1个0,两个取相反那就是不满足的条件m<n-1||m>2*(n+1)

其他的我们可以先把0摆好，然后每个1放0后面，放完之后还有1，我们可以向在开头放两个1，m-=2,如何放01的后面组成011，最后放多的1；

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

int main()
{
    int n,m;
    cin>>n>>m;
    if(m<n-1||m>2*(n+1)) puts("-1");
    else
    {
        for(int i=0;i<2;i++)
            if(m>n-1)
            {
                cout<<1;
                m--;
            }
        while(n)
        {
            cout<<0;
            n--;
            if(n)
            {
                cout<<1;
                m--;
                if(m>n-1)
                {
                    cout<<1;
                    m--;
                }
            }
            while(m--) cout<<1;
        }
    return 0;
}