文章目录
- 引言
- 二、幂级数
- 2.1 基本概念
- 2.2 幂级数的收敛半径与收敛域
- 2.3 幂级数的性质
- 2.4 将函数展开为幂级数
- 2.4.1 直接法
- 2.4.2 间接法
- 2.5 求幂级数的和函数
- 写在最后
引言
承接前文的常数项级数,我们来继续看看关于幂级数的内容。
二、幂级数
2.1 基本概念
函数项级数 —— 设 { u n ( x ) } \{u_n(x)\} {un(x)} 为函数列,称 ∑ n = 1 ∞ u n ( x ) \sum_{n=1}^\infty u_n(x) ∑n=1∞un(x) 为函数项级数。当 x = x 0 x=x_0 x=x0 时,若常数项级数 ∑ n = 1 ∞ u n ( x 0 ) \sum_{n=1}^\infty u_n(x_0) ∑n=1∞un(x0) 收敛,称 x = x 0 x=x_0 x=x0 为函数项级数的收敛点;若 ∑ n = 1 ∞ u n ( x 0 ) \sum_{n=1}^\infty u_n(x_0) ∑n=1∞un(x0) 发散,称 x = x 0 x=x_0 x=x0 为发散点。所有收敛点组成的集合称为收敛域,所有发散点组成的集合为发散域。记 S n ( x ) = u 1 ( x ) + u 2 ( x ) + ⋯ + u n ( x ) S_n(x)=u_1(x)+u_2(x)+\dots+u_n(x) Sn(x)=u1(x)+u2(x)+⋯+un(x) ,在收敛域内,设 S ( x ) = lim S n ( x ) S(x)=\lim S_n(x) S(x)=limSn(x) ,称 S ( x ) S(x) S(x) 为和函数。
看得头大了,举一个实例增进理解。比如当 u n ( x ) = x / n u_n(x)=x/n un(x)=x/n 时,那么 { u n ( x ) } = { x , x / 2 , x / 3 , … x / n , … } \{u_n(x)\}=\{x,x/2,x/3,\dots x/n,\dots\} {un(x)}={x,x/2,x/3,…x/n,…} ,如果 x = 1 x=1 x=1 ,该级数就变为一个常数项级数 { 1 , 1 / 2 , … , 1 / n , … } \{1,1/2,\dots,1/n,\dots \} {1,1/2,…,1/n,…} 。
幂级数 —— 形如 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 或 ∑ n = 0 ∞ a n ( x − x 0 ) n \sum_{n=0}^\infty a_n(x-x_0)^n ∑n=0∞an(x−x0)n 的级数称为幂级数。
2.2 幂级数的收敛半径与收敛域
定理 1(阿贝尔定理) —— 对于幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn ,当 x = x 0 ( x 0 ≠ 0 ) x=x_0(x_0 \ne 0) x=x0(x0=0) 时,幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 收敛,则当 ∣ x ∣ < ∣ x 0 ∣ |x|<|x_0| ∣x∣<∣x0∣ 时,幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 绝对收敛;当 x = x 1 x=x_1 x=x1 时,幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 发散,则当 ∣ x ∣ > ∣ x 1 ∣ |x|>|x_1| ∣x∣>∣x1∣ 时,幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 发散。
由阿贝尔定理,对于任何一个幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn ,总存在 R ≥ 0 R \geq 0 R≥0 ,当 ∣ x ∣ < R |x| < R ∣x∣<R 时, ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 绝对收敛;当 ∣ x ∣ > R |x| >R ∣x∣>R 时,幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 发散,称 R R R 为幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 的收敛半径。
定理 2 —— 对于幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 及其收敛半径 R R R ,设 lim n → ∞ ∣ a n + 1 a n ∣ = ρ , \lim_{n\to\infty}\big|\frac{a_{n+1}}{a_n}\big|=\rho, n→∞lim anan+1 =ρ, 则当 ρ = 0 \rho=0 ρ=0 时, R = + ∞ R=+\infty R=+∞ ;当 ρ = + ∞ \rho=+\infty ρ=+∞ 时, R = 0 R=0 R=0 ;当 0 < ρ < + ∞ 0<\rho<+\infty 0<ρ<+∞ 时, R = 1 / ρ . R=1/\rho. R=1/ρ.
定理 3 —— 对于幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^n ∑n=0∞anxn 及其收敛半径 R R R ,设 lim n → ∞ ∣ a n ∣ n = ρ , \lim_{n\to\infty}\sqrt[n]{|a_n|}=\rho, n→∞limn∣an∣=ρ, 则当 ρ = 0 \rho=0 ρ=0 时, R = + ∞ R=+\infty R=+∞ ;当 ρ = + ∞ \rho=+\infty ρ=+∞ 时, R = 0 R=0 R=0 ;当 0 < ρ < + ∞ 0<\rho<+\infty 0<ρ<+∞ 时, R = 1 / ρ . R=1/\rho. R=1/ρ.
一些笔记:
对于幂级数 ∑ n = 0 ∞ a n x 3 n \sum_{n=0}^\infty a_nx^{3n} ∑n=0∞anx3n ,设 lim n → ∞ ∣ a n + 1 a n ∣ = ρ \lim_{n\to\infty}\big|\frac{a_{n+1}}{a_n}\big|=\rho limn→∞ anan+1 =ρ ,则 R = 1 / ρ 3 R=\sqrt[3]{1/\rho} R=31/ρ ;同理,对于 f ( x ) = ∑ n = 0 ∞ a n x 2 n + 1 f(x)=\sum_{n=0}^\infty a_nx^{2n+1} f(x)=∑n=0∞anx2n+1 ,若 lim n → ∞ ∣ a n + 1 a n ∣ = ρ \lim_{n\to\infty}\big|\frac{a_{n+1}}{a_n}\big|=\rho limn→∞ anan+1 =ρ ,则 R = 1 / ρ 2 R=\sqrt[2]{1/\rho} R=21/ρ .
若对于幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^{n} ∑n=0∞anxn ,当 x = x 0 x=x_0 x=x0 时,幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^{n} ∑n=0∞anxn 条件收敛,则 R = ∣ x 0 ∣ . R=|x_0|. R=∣x0∣.
幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^{n} ∑n=0∞anxn 与 ∑ n = 0 ∞ a n ( x − x 0 ) n \sum_{n=0}^\infty a_n(x-x_0)^{n} ∑n=0∞an(x−x0)n 收敛半径相同,但前者收敛域以 x = 0 x=0 x=0 为中心,后者收敛域以 x = x 0 x=x_0 x=x0 为中心。
2.3 幂级数的性质
设幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^{n} ∑n=0∞anxn 的收敛半径为 R R R ,其和函数为 S ( x ) S(x) S(x) ,则有如下定理。
定理 1 —— 幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^{n} ∑n=0∞anxn 的和函数 S ( x ) S(x) S(x) 在 ( − R , R ) (-R,R) (−R,R) 上连续。
若幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^{n} ∑n=0∞anxn 在 x = − R x=-R x=−R 处收敛,则幂级数 ∑ n = 0 ∞ a n ( − R ) n \sum_{n=0}^\infty a_n(-R)^{n} ∑n=0∞an(−R)n 收敛于 lim x → − R + S ( x ) \lim_{x\to -R^+}S(x) limx→−R+S(x) ,即 ∑ n = 0 ∞ a n ( − R ) n = S ( − R + 0 ) \sum_{n=0}^\infty a_n(-R)^{n}=S(-R+0) ∑n=0∞an(−R)n=S(−R+0) ;
若幂级数 ∑ n = 0 ∞ a n x n \sum_{n=0}^\infty a_nx^{n} ∑n=0∞anxn 在 x = R x=R x=R 处收敛,则幂级数 ∑ n = 0 ∞ a n R n \sum_{n=0}^\infty a_nR^{n} ∑n=0∞anRn 收敛于 lim x → R − S ( x ) \lim_{x\to R^-}S(x) limx→R−S(x) ,即 ∑ n = 0 ∞ a n R n = S ( R − 0 ) \sum_{n=0}^\infty a_nR^{n}=S(R-0) ∑n=0∞anRn=S(R−0) ;
定理 2(逐项可导性) —— 当 x ∈ ( − R , R ) x\in(-R,R) x∈(−R,R) 时,有 ( ∑ n = 0 ∞ a n x n ) ′ = ∑ n = 0 ∞ ( a n x n ) ′ = ∑ n = 0 ∞ n a n x n − 1 , \big(\sum_{n=0}^\infty a_nx^n\big)'=\sum_{n=0}^\infty (a_nx^n)'=\sum_{n=0}^\infty na_nx^{n-1}, (n=0∑∞anxn)′=n=0∑∞(anxn)′=n=0∑∞nanxn−1, 且幂级数 ∑ n = 0 ∞ n a n x n − 1 \sum_{n=0}^\infty na_nx^{n-1} ∑n=0∞nanxn−1 的收敛半径也为 R R R 。
定理 3(逐项可积性) —— 当 x ∈ ( − R , R ) x\in(-R,R) x∈(−R,R) 时,有 ∫ 0 x ( ∑ n = 0 ∞ a n x n ) d x = ∑ n = 0 ∞ ∫ 0 x a n x n d x = ∑ n = 0 ∞ a n n + 1 x n + 1 , \int_0^x\big(\sum_{n=0}^\infty a_nx^n\big)dx=\sum_{n=0}^\infty \int_0^xa_nx^ndx=\sum_{n=0}^\infty \frac{a_n}{n+1}x^{n+1}, ∫0x(n=0∑∞anxn)dx=n=0∑∞∫0xanxndx=n=0∑∞n+1anxn+1, 且幂级数 ∑ n = 0 ∞ a n n + 1 x n + 1 \sum_{n=0}^\infty \frac{a_n}{n+1}x^{n+1} ∑n=0∞n+1anxn+1 的收敛半径也为 R R R 。
注意,对幂级数逐项求导或积分后的级数尽管与原级数收敛半径相同,但收敛域不一定相同。
2.4 将函数展开为幂级数
2.4.1 直接法
其实就是泰勒展开到无穷项,回忆下我们的泰勒中值定理,就能理解了。

需要记忆以下函数的幂级数展开。
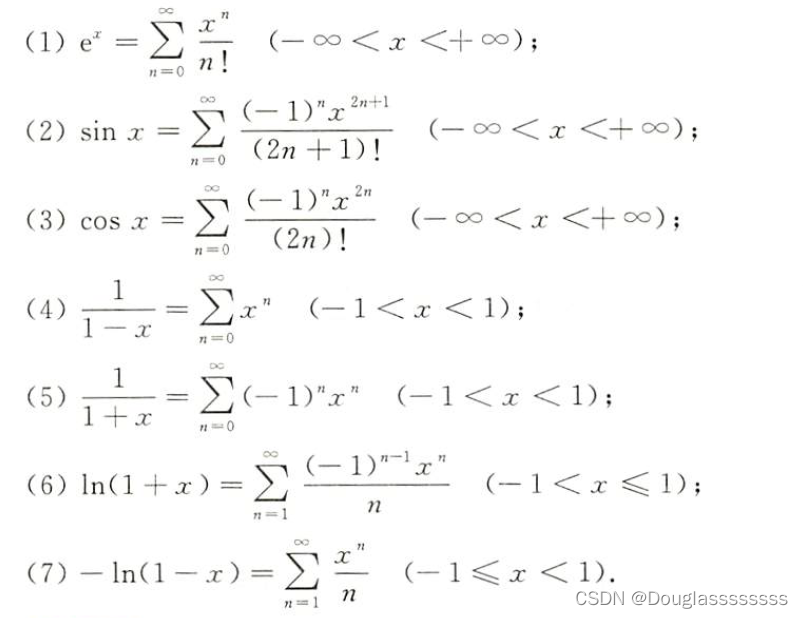
2.4.2 间接法
通常指使用如下两个工具求函数的幂级数展开式。
(1)常见函数的麦克劳林级数;
(2)幂级数的逐项可导性和逐项可积性。
2.5 求幂级数的和函数
求和函数本质上是函数展开为为幂级数的逆过程,通常需要使用如下三个工具:
(1)常见函数的麦克劳林级数;
(2)幂级数的逐项可导性和逐项可积性;
(3)微分方程。
写在最后
可以回忆起刚学那会,就是幂级数这一块要命,希望这次能顺利掌握。
后面还有一个傅里叶级数,讲道理,之前学自动控制原理和看一些人用傅里叶级数画很好看的图的时候,我就想去系统学学了,也想着去画一画有意思的图。








![java八股文面试[数据库]——MySQL中事务的特性](https://img-blog.csdnimg.cn/img_convert/92a2d596049eb4ff98645af6094bc9d1.png)
![[移动通讯]【Carrier Aggregation-3】【5G】](https://img-blog.csdnimg.cn/03095eed827a410182e1a8f74c76bed2.png)