「通信原理」格雷码的生成与破译

格雷码，gray code，相邻两数之间只有一个bit发生了改变，因此相比于自然编码的二进制系统，格雷编码的更不容易出错。使用卡诺图化简布尔代数式的时候，也会用到格雷码。本文将介绍三种格雷码的生成与破译方法，即格雷码和自然编码的相互转换。格雷码的顺序不是唯一的。

1、直接排列

根据定义直接排列，适用于十分简单的情形。

十进制	二进制（自然编码）	格雷码
0	00	00
1	01	01
2	10	11
3	11	10

2、镜射法

n位的格雷码可以直接由n-1位的格雷码“镜面反射”之后，在前面添加0或者1直接得到。其过程如下图所示：

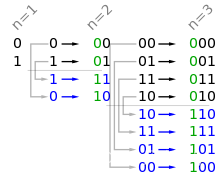
第二列的[0 1 1 0]即是1位格雷码“镜面反射”得到的，然后在前面添加[0 0 1 1]则得到2位的格雷码[00, 01, 11, 10]。同理可得3位的格雷码。

3、公式法：

（1）二进制数转格雷码

前面两种方法都是适用于位元数较小的二进制数，当n很大时（一张纸写不下的时候），就不适合列举出所有的对应关系，再去编解码了。

符号规定：G：格雷码，B：二进制码，k：正在计算的位

生成公式：G(k) = B(k+1) ⊕ B(k)或者G(k) = B(k+1) +B(k)

文字解释：第k位的格雷码🟰自然编码的第k位 异或 第k+1位。

注意：

1. 异或：相异为1，相同为0；或称为模2加、二进制加法。
2. n+1位：对于n位的自然编码，第n+1位为0。
3. 从低位向高位运算。

举例：求6对应的格雷码。
6的自然二进制编码为110。格雷码也将有3bit，G(1) = B(2)+B(1)=1, G(2) = B(3)+B(2) = 0, G(3) = B(4)+B(3) = 1
则格雷编码为101。

（2）格雷码转二进制数

反过来：B(k) = G(k) - B(k+1) ，或者B(k) = G(k) + B(k+1) 、B(k) = G(k) ⊕ B(k+1)

注意：

1. 模2减的运算规则和模2加一模一样。
2. 从高位向低位运算。

举例：求101对应的自然编码。
格雷码为101，B(3) = G(3)+B(4)=1, B(2) = G(2)+B(3) = 1, B(1) = G(1)+B(2) = 0。
则自然编码为110。

4、线性变换法

（1）二进制数转格雷码

二进制码转换为格雷码，可以看成是一种线性变换T：$V_n(B)\to V_n(B)$。（假设用B来表示0和1）

对于一个4bit的二进制空间，所有坐标为：{0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111}。基为(e1, e2, e3, e4)。e1 = [1,0,0,0]^T，e2 = [0,1,0,0]^T，e3 = [0,0,1,0]^T，e4 = [0,0,0,1]^T。任何一个二进制数B = (e1, e2, e3, e4)x。x是这个二进制数的坐标，是一个列向量。

对于一个4bit的格雷编码的空间。基为(g1, g2, g3, g4)。g1 = [1,1,0,0]^T，g2 = [0,1,1,0]^T，g3 = [0,0,1,1]^T，g4 = [0,0,0,1]^T

根据线性变换的规则，T(e1) = g1 = e1+e2, T(e2) = g2 = e2+e3, T(e3) = g3 = e3+e4, T(e4) = g4 = e4。

写成矩阵的形式：T(e1, e2, e3, e4) = (g1, g2, g3, g4) = (e1, e2, e3, e4)A

A = array([[1, 0, 0, 0],

​ [1, 1, 0, 0],

​ [0, 1, 1, 0],

​ [0, 0, 1, 1]])

所有的4bit格雷码，都可以通过A来生成。

举例：12的格雷码。
12的坐标为x=[1,1,0,0]T
Ax = [1,0,1,0]T
注意：这里是二进制乘法。

（2）格雷码转二进制数

反过来，只需要求出线性变换的逆矩阵，A^-1即可。用A^-1乘以格雷码向量，即可转换为相应的自然编码。

举例：[1,0,1,0]T的自然编码。
A- = array([[ 1.,  0.,  0.,  0.],
       [-1.,  1.,  0.,  0.],
       [ 1., -1.,  1.,  0.],
       [-1.,  1., -1.,  1.]])
注意这里是二进制乘法，因此-1应该写成1，2应该写成0
所以，A- =array([[ 1,  0,  0,  0],
       [ 1,  1, 0,  0],
       [ 1,  1, 1,  0],
       [ 1,  1, 1,  1]]) 
np.dot(A-,[1,0,1,0]) = array([1, 1, 2, 2]) = [1,1,0,0]T

---

总结：本文一共用了四种方法来构造格雷码，其中前三种都是在传统的通信专业课程里面会学习到，第四种是在研究生课程矩阵理论当中会学到（数学专业可能在本科就会学习到）。