我们今天遇到的大多数软件产品都集成了某种形式的搜索功能。我们在谷歌上搜索内容,在YouTube上搜索视频,在亚马逊上搜索产品,在Slack上搜索信息,在Gmail上搜索邮件,在Facebook上搜索人等等。

作为用户,工作流非常简单。我们可以通过在搜索框中写下我们的查询来搜索条目,系统中的排名模型会给我们最相关的前n个结果。
我们如何评估前n个结果有多好?
在这篇文章中,我将解释学习中常用的离线度量来回答上述问题。这些指标不仅对评估搜索结果有用,而且对关键字提取和推荐等问题也有用。
问题1:二元相关性
让我们通过一个简单的玩具例子来理解各种评估指标的细节和权衡。我们有一个排序模型,它会为一个特定的查询返回5个最相关的结果。根据我们的ground-truth,第一个、第三个和第五个结果是相关的。

让我们看看评估这个简单例子的各种指标。
A. 排序不感知的度量
1. Precision@k
这个指标量化了排名前k的结果中有多少项是相关的。在数学上,由下式给出:

对于我们的例子,precision@1 = 1,因为前1结果中的所有项都是相关的。

同样,precision@2 = 0.5,因为前2个结果中只有一个是相关的。
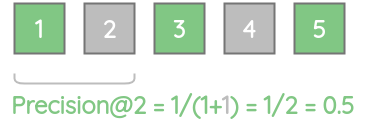
我们可以计算出所有k值的precision分数。

precision@k的一个限制是它没有考虑相关的项目的位置。考虑具有相同数量相关结果的两个模型A和B,即5个中的3个。对于模型A,前三项是相关的,而对于模型B,后三项是相关的。尽管模型A更好,但对于这两个模型,Precision@5是相同的。

2. Recall@k
这个度量给出了查询的所有实际相关结果中在所有的实际的相关结果中的比例。在数学上:
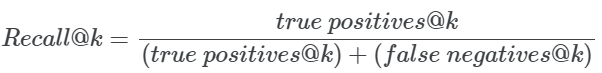
对于我们的例子,recall@1 = 0.33,因为只存在3个实际相关项中的一个。
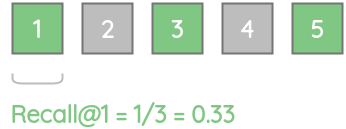
类似地,由于3个实际相关的项中只有2个项存在,故recall@3 = 0.67。
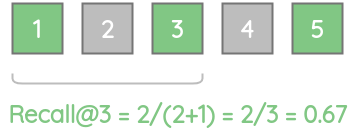
我们可以计算不同K值的召回分数。
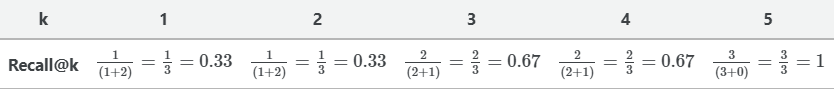
3. F1@k
这是一个组合度量,通过取它们的调和平均值,将Precision@k和Recall@k结合在一起。我们可以这样计算:

利用前面计算的precision和recall的值,我们可以计算不同K值的F1-scores,如下图所示。

B. 排序感知的度量
虽然precision、recall和F1为我们提供了一个单值度量,但它们不考虑返回的搜索结果的顺序。为了解决这一局限性,人们设计了以下排序感知的度量标准:
1. Mean Reciprocal Rank(MRR)
当我们希望系统返回最佳相关项并希望该项位于较高位置时,这个度量是有用的。
在数学上:
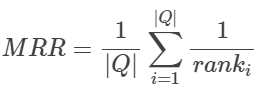
其中:
-
‖Q‖表示查询的总数
-
ranki表示第一个相关结果的排序
为了计算MRR,我们首先计算排序倒数。它只是第一个正确的相关结果的倒数,值的范围从0到1。
在我们的例子中,由于第一个正确的项目位于1的位置,所以1的倒数为1。

让我们看另一个例子,其中只有一个相关结果出现在列表的最后,即位置5。它的倒数得分更低,为0.2。

让我们考虑另一个例子,其中返回的结果都不相关。在这种情况下,倒数为0。

对于多个不同的查询,我们可以通过对每个查询取倒数的平均值来计算MRR。
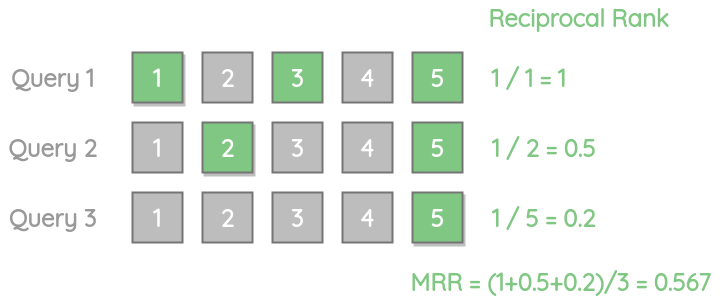
我们可以看到,MRR并不关心剩余的相关结果的位置。所以,如果你的例子需要以最好的方式返回多个相关的结果,MRR不是一个合适的度量。
2. Average Precision(AP)
平均精度是衡量模型选择的所有与 ground-truth相关的项目是否都有较高的排序。与MRR不同,它考虑所有相关的项目。
数学上:
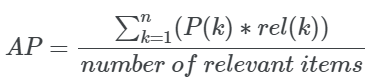
其中:
-
rel(k)是一个指示函数,当第k位的项有相关性时为1。
-
P(k)是Precision@k度量
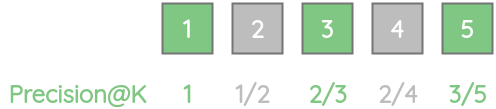
对于我们的例子,我们可以根据不同K的Precision@K值计算AP。
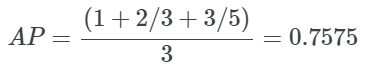
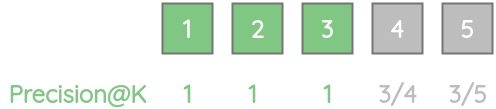
为了说明AP的优势,让我们以前面的例子为例,但将3个相关的结果放在开头。我们可以看到,这个例子比上面的例子获得了一个更好的AP分数。
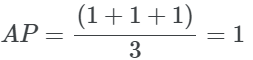
3. Mean Average Precision(MAP)
如果我们想计算多个查询的平均精度,我们可以使用MAP。它只是所有查询的平均精度的平均值。数学上:
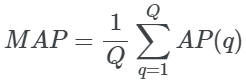
其中:
-
Q是查询的总数
-
AP(q)是查询q的平均精度
python原代码实现
def average_precision(true_labels, predicted_scores):
sorted_results = [(true, score) for true, score in
sorted(zip(true_labels, predicted_scores), key=lambda x: x[1], reverse=True)]
num_true = sum(true_labels)
precision_at_k = []
true_positives = 0
for i, (true, score) in enumerate(sorted_results):
if true == 1:
true_positives += 1
precision_at_k.append(true_positives / (i + 1))
if not precision_at_k:
return 0.0
return sum(precision_at_k) / num_true
def map_at_k(true_labels, predicted_scores, k):
average_precisions = []
for i in range(len(true_labels)):
ap = average_precision(true_labels[i][:k], predicted_scores[i][:k])
average_precisions.append(ap)
return sum(average_precisions) / len(average_precisions)
# 示例数据,真实标签和模型的预测分数(多个查询)
true_labels = [[1, 0, 1, 1, 0, 0, 1, 1, 0, 0], [0, 1, 1, 0, 1, 0, 0, 1, 1, 0]]
predicted_scores = [[0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.0],
[0.9, 0.8, 0.5, 0.4, 0.8, 0.2, 0.1, 0.9, 0.3, 0.0]]
# 计算平均精确度(Average Precision)
average_precision_1 = average_precision(true_labels[0], predicted_scores[0])
average_precision_2 = average_precision(true_labels[1], predicted_scores[1])
print("Average Precision 1:", average_precision_1)
print("Average Precision 2:", average_precision_2)
# 计算MAP@k
k = 5
map_at_k= map_at_k(true_labels, predicted_scores, k)
# map_at_k_2 = map_at_k(true_labels[1], predicted_scores[1], k)
print(f"MAP@{k}:", map_at_k)
使用sklearn实现
from sklearn.metrics import average_precision_score
# 示例数据,真实标签和模型的预测分数
true_labels = [1, 0, 1, 1, 0, 0, 1, 1, 0, 0]
predicted_scores = [0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.0]
# 计算平均精确度(Average Precision)
average_precision = average_precision_score(true_labels, predicted_scores)
print("Average Precision:", average_precision)
问题2: 分等级的相关性
让我们以另一个玩具例子为例,其中我们不仅标注了相关或不相关的项目,而是使用了0到5之间的评分标准,其中0表示相关性最低,5表示相关性最高。

我们有一个排序模型,它会为一个特定的查询返回5个最相关的结果。根据我们的ground-truth,第一项的相关性得分为3,第二项的相关性得分为2,以此类推。
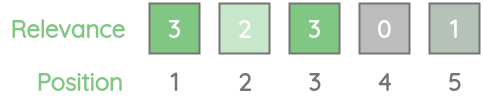
让我们了解评估这种类型的各种度量。
1. Cumulative Gain (CG@k)
这个度量使用了一个简单的概念来总结top-K条目的相关性分数。这个总分数称为累积收益。在数学上:
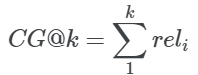
对于我们的例子,CG@2是5,因为我们将前两个相关性得分3和2相加。
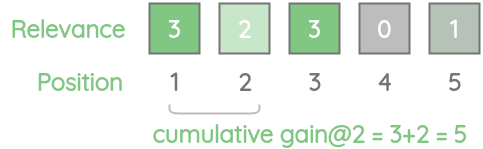
同理,我们可以计算所有k值的累积收益:
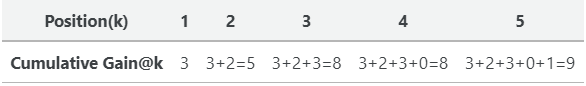
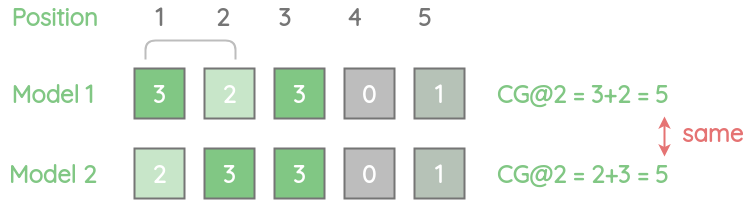
虽然很简单,但CG并没有考虑到相关项目的顺序。因此,即使我们将一个不太相关的项交换到第一个位置,CG@2也是一样的。
2. Discounted Cumulative Gain (DCG@k)
我们看到了一个简单的累积收益是如何不考虑位置的。但是,我们通常希望具有高相关性得分的项目出现在一个更好的排序位置上。
考虑下面的一个例子。在累积收益的情况下,我们只是简单地将分数相加,而没有考虑它们的位置。
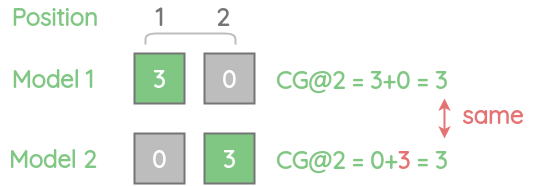
一个物品在位置1上,相关分数为3要比相同的物品在位置2上相关分数为3要好。
所以,我们需要一些方法来惩罚他们的位置。DCG引入了一个基于对数的惩罚函数来降低每个位置的相关性得分。对于5个项,惩罚是:

使用这个惩罚,我们现在可以计算折扣累积收益,只需使用惩罚标准化过后的相关分数的总和。在数学上:

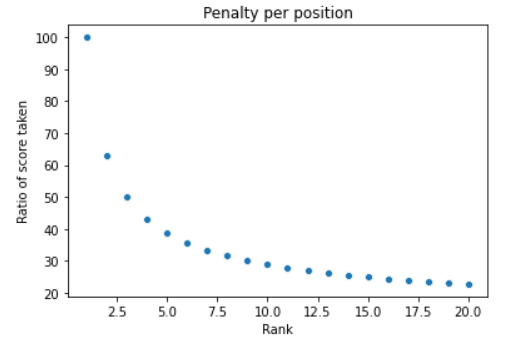
为了理解对数惩罚的行为,让我们在x轴上绘制排名位置,在y轴上绘制相关性得分的百分比,即
![]()
。正如所看到的,在位置1,我们不施加任何惩罚,分数保持不变。但是,分数的百分比指数递减从第1位的100%到第2位的63%,第3位的50%,以此类推。
现在为我们的例子计算DCG。

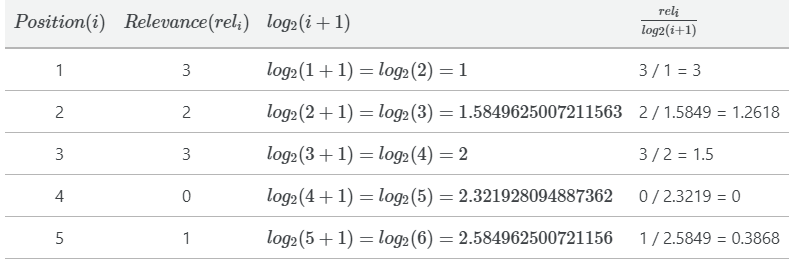
基于这些惩罚过的分数,我们现在可以计算不同k值下的DCG,只需将它们加起来。
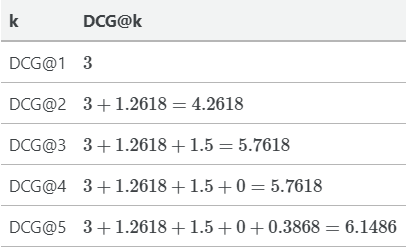
对于DCG@K还有一种替代公式,如果相关的条目排名较低,那么惩罚就会更多。该方案在工业上更受青睐。

虽然DCG解决了累积收益的问题,但它有一定的局限性。假设查询Q1有3个结果,查询Q2有5个结果。那么有5个结果Q2的查询将会有一个更大的总体DCG分数。但我们不能说问题2比问题1好。
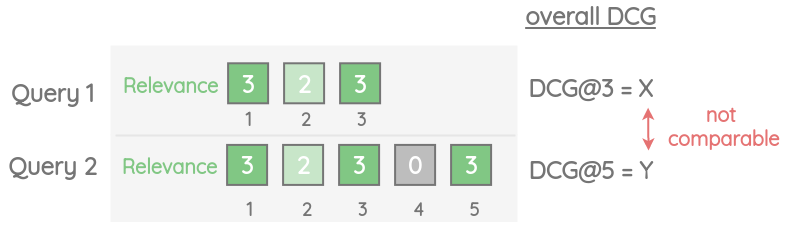
3. Normalized Discounted Cumulative Gain (NDCG@k)
为了允许跨查询比较DCG,我们可以使用NDCG,它使用相关项的理想顺序来规范化DCG值。让我们以之前的例子为例,我们已经计算了不同K值下的DCG值。

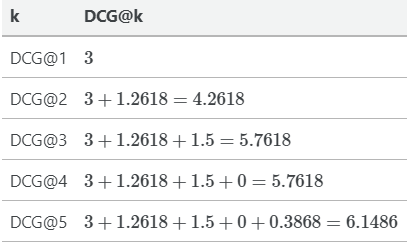
对于我们的例子,理想情况下,我们希望条目按照相关性得分的降序排序。
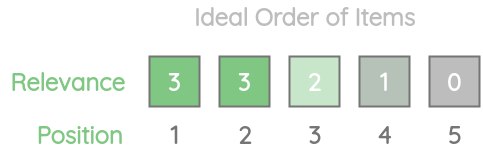
我们来计算这个排序下的理想的DCG(IDCG)。

现在,我们可以计算不同k的NDCG@k,通过对DCG@k除以 IDCG@k:
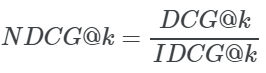
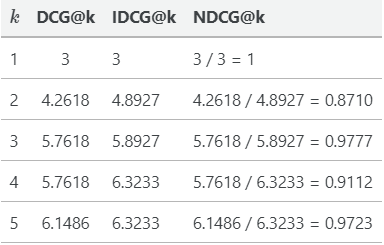
因此,我们得到的NDCG分数的范围在0到1之间。一个完美的排名会得到1分。我们还可以比较不同查询的NDCG@k分数,因为它是一个标准化分数。
总结
这篇文章中,我们了解了二元相关性和分级标签相关性的各种评估指标,以及每个指标如何改进之前的指标
英文原文:https://amitness.com/2020/08/information-retrieval-evaluation/


![java八股文面试[数据库]——数据库锁的种类](https://img-blog.csdnimg.cn/img_convert/c148b1baee7458a8bd8633784d707845.png)
![开店星小程序上架教程和后台Request failed with status code 500[undefined]问题处理](https://img-blog.csdnimg.cn/0ffa63b0c751464ea616546541f65253.jpeg)


![[SSM]MyBatisPlus高级](https://img-blog.csdnimg.cn/c80537e7433f46ea882c0f98da3fe269.png)