需要源码和数据集请点赞关注收藏后评论留言私信~~~

模型聚类

模型（Model）聚类假定每个簇符合一个分布模型，通过找到这个分布模型，就可以对样本点进行分簇。

在机器学习领域，这种先假定模型符合某种概率分布（或决策函数），然后在学习过程中学习到概率分布参数（或决策函数参数）的最优值的模型，称为参数学习模型。

模型聚类主要包括概率模型和神经网络模型两大类，前者以高斯混合模型（Gaussian Mixture Models，GMM）为代表，后者以自组织映射网络（Self Organizing Map，SOM）为代表。

高斯混合模型GMM

记随机变量X服从含有未知变量τ=(μ,σ^2)的高斯分布，其概率密度为：

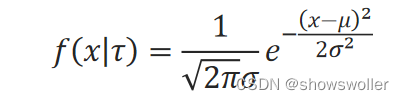
高斯混合模型P(├ x|θ)是多个高斯分布混合的模型：

 

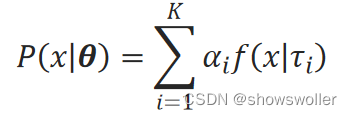
式中，K是混合的高斯分布的总数，τ_i是第i个高斯分布的未知变量，记τ=(τ_1,τ_2,…,τ_K)。α_i是第i个高斯分布的混合系数，α_i>0，∑▒α_i=1，α_i可看作概率值，记α=(α_1,α_2,…,α_K)。记θ=(α，τ)。

将高斯混合模型用于聚类任务时，认为样本是由P(├ x|θ)产生的，产生的过程是先按概率α选择一个高斯分布f(├ x|τ_j)，再由该高斯分布生成样本。

由同一高斯分布产生的样本属于同一簇，即高斯混合模型中的高斯分布与聚类的簇一一对应。

在分簇过程中，算法的任务是从训练集中学习到模型参数θ=(α，τ)，在分配过程，模型计算测试样本由每个高斯分布产生的概率，取最大概率对应的高斯分布的簇作为分配的簇。

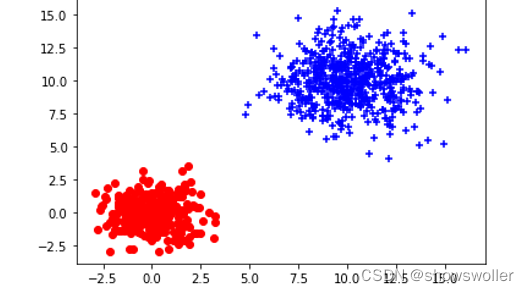
以（0，0）和（10，10）为中心，以1.2和1.8为标准差，分别生成两个簇。

本次示例中，生成的两个簇是完全间隔开的，观察模型学习到的均值和方差是非常小的，由此可见误差比较小

 

 代码如下

X1, y1 = make_blobs(n_samples=300, n_features=2, centers=[[0,0]], cluster_std=[1.2])
X2, y2 = make_blobs(n_samples=600, n_features=2, centers=[[3,3]], cluster_std=[1.8])
plt.scatter(X1[:, 0], X1[:, 1], marker='o', color='r')
plt.scatter(X2[:, 0], X2[:, 1], marker='+', color='b')
plt.show()

下面是将两个簇的一部分重合的效果

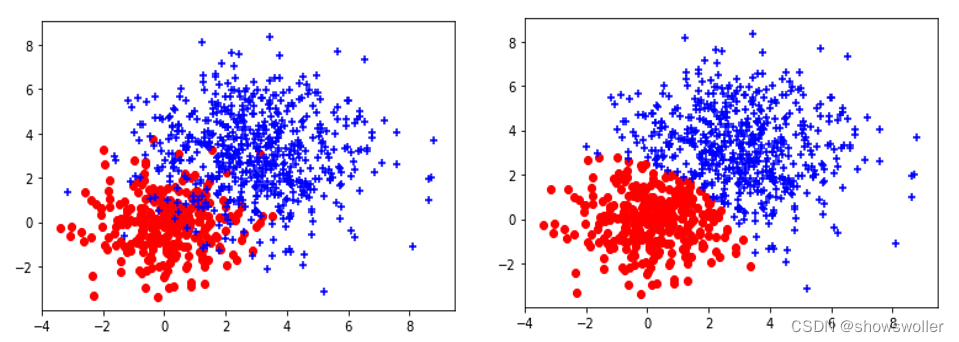
这次均值和协方差都变大了很多，由此可见 高斯混合聚类对重合部分的点并不能很好的预测，分簇结果有一条明显的分界线，该分界线是两个模型计算概率值相等的地方

下面对txt文件中的点的坐标进行高斯混合聚类分析的效果如下

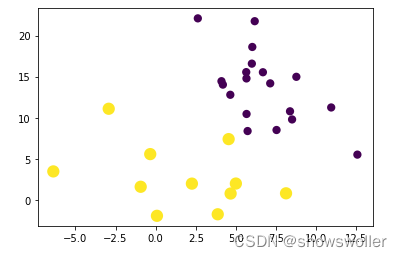
代码如下

from sklearn.mixture import GaussianMixture
import numpy as np
samples = np.loadtxt("kmeansSamples.txt")
gm = GaussianMixture(n_components=2, random_state=0).fit(samples)
labels = gm.predict(samples)
import matplotlib.pyplot as plt
plt.scatter(samples[:,0],samples[:,1],c=labels+1.5,linewidths=np.power(labels+1.5, 2))
plt.show()

 创作不易 觉得有帮助请点赞关注收藏~~~