【 声明：版权所有，欢迎转载，请勿用于商业用途。 联系信箱：feixiaoxing @163.com】

        学习SLAM，离开了矩阵肯定是玩不转的。大学数学里面除了微积分，剩下的就是线性代数和概率论。而矩阵就是线性代数的一部分。到了研究生，高等数学不学了，但是会继续学习矩阵论和随机数学。它们是线性代数和概率论的衍生。很多同学可能会说，学习矩阵有什么用？主要还是为了解决问题，方便描述。

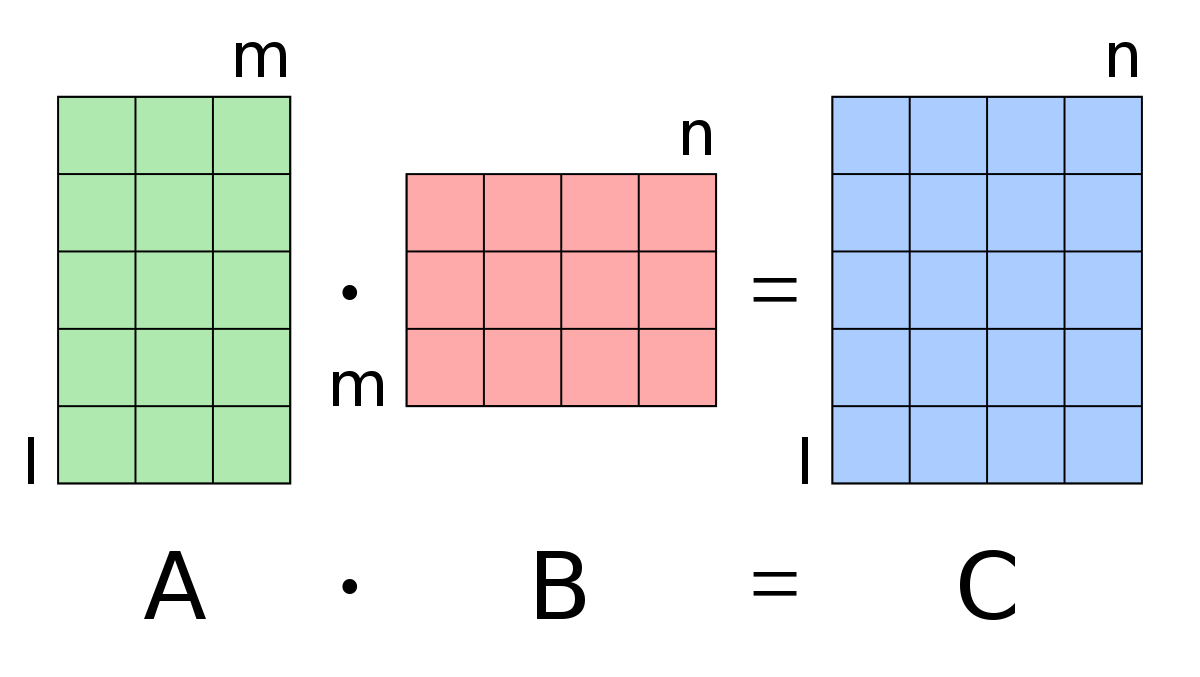
1、一个二元一次方程

        所谓的二元一次方程，写成公式就是这样的形式，这里假设num是一个常数。

        看上去一切还算正常。学过几何的同学都知道这是一条直线，那么假设我们知道了两组（x，y），是不是就可以画出这个直线了，

        这是一个简单的二元一次方程。简单解一下，可以算出来a=1，b=1。

2、用矩阵怎么描述

        虽然是一个简单的二元一次方程，但是也是可以用矩阵来描述的。还是上面这么一个情况，如果用矩阵描述，是这样的，

3、用矩阵该怎么解

        学过矩阵的同学都知道，按照上面的公式，如果需要求解a和b，那么就要在等式的两边乘以一个逆。这个逆就是矩阵[4 1; 1 4]的逆。所以，a、b的求解是这样的，

4、怎么用计算机来解决矩阵的逆

        怎么用计算机来求解逆，这确实是一个问题。不过计算机求解，一般和个人计算是不一样的。计算机的求解大部分是用优化的方法去逼近一个标准答案。而个人如果是完成作业，或者是考试求解逆，则是按照标准的计算流程一步一步去完成。这里，我们可以先安装eigen3-dev的库，

sudo apt-get install libeigen3-dev

        确认矩阵库已经没有问题之后，这个时候就可以编写代码了，

#include <iostream>
#include <eigen3/Eigen/Dense>
using Eigen::MatrixXd;

int main()
{
	MatrixXd m(2,2);
	MatrixXd n(2,1);
	m(0,0) = 4;
	m(1,0) = 1;
	m(0,1) = 1;
	m(1,1) = 4;

	n(0,0) = 5;
	n(1,0) = 5;

	MatrixXd param(2,1);
	param = m.inverse() * n;
	std::cout << param << std::endl;
	return 0;
}

        代码本身其实没有什么复杂的，m就代表了整个矩阵，是2行*2列。n代表了最终的数值，是2行*1列。而中间的param则代表了中间的参数，也是2行*1列。整个计算过程，最重要的一句话就是param = m.inverse() * n，m.inverse代表先求解矩阵的逆，然后再和n进行相乘。相乘的结果就是param，其中a=param(0,0)，b=param(1,0)。

$ ./eigen 
1
1

        在这计算过程中，对于行和列，一定要分清楚，弄不好，你就看到这样的打印，

$ ./eigen 
eigen: /usr/include/eigen3/Eigen/src/Core/Product.h:95: Eigen::Product<Lhs, Rhs, Option>::Product(const Lhs&, const Rhs&) [with _Lhs = Eigen::Inverse<Eigen::Matrix<double, -1, -1> >; _Rhs = Eigen::Matrix<double, -1, -1>; int Option = 0; Eigen::Product<Lhs, Rhs, Option>::Lhs = Eigen::Inverse<Eigen::Matrix<double, -1, -1> >; Eigen::Product<Lhs, Rhs, Option>::Rhs = Eigen::Matrix<double, -1, -1>]: Assertion `lhs.cols() == rhs.rows() && "invalid matrix product" && "if you wanted a coeff-wise or a dot product use the respective explicit functions"' failed.

        看到这种输出，不要怀疑，直接就是行和列搞反了。

5、SLAM中使用矩阵最终的目的

        关于矩阵，大部分SLAM处理的时候都可以看到这样的方程，即

watch_data * pose = real_data
min(sigma(ground_truth - real_data))

        这里的watch_data是一个矩阵，pose是最终目标，可以认为是局部空间里面找一个最佳结果。而real_data，则是该矩阵的计算结果。此外，对于每个watch_data，它的ground_truth数值，我们都是知道的，所以这里的计算目标就变成求解一个pose，使得它的real_data和ground_truth之间的累计和最小。这就是SLAM pose求解的意义。