需要全部代码请点赞关注收藏后评论区留言私信~~~

维数灾难

维数灾难是指在涉及到向量计算的问题中，当维数增加时，空间的体积增长得很快，使得可用的数据在空间中的分布变得稀疏，向量的计算量呈指数倍增长的一种现象。维数灾难涉及数值分析、抽样、组合、机器学习、数据挖掘和数据库等诸多领域。

降维不仅可以减少样本的特征数量，还可以用来解决特征冗余（是指不同特征有高度相关性）等其他数据预处理问题。可视化并探索高维数据集也是它的一个重要应用。

降维算法是专门用于降维的算法，可以分为线性和非线性的，线性的降维算法是基于线性变换来降维，主要有奇异值分解，主成分分析等算法，主成分分析是最常用的降维算法，下面我们将重点讨论它

主成分分析PCA

1：二维数据降维

顾名思义，主成分分析是指找出主要成分来代替原始数据，用二维平面上的例子来简要说明其过程

在二维平面上有x_1,x_2,x_3,x_4四个点，坐标分别是（4，2）、（0，2）、（-2，0）和（-2，-4），它们满足所谓中心化要求，即∑_i=1^4▒x_i=0。对不满足中心化要求的点，可通过减所有点的均值来满足该要求

降维必定会带来误差，如何使总体误差最小是降维算法追求的目标。用所有误差向量的模的平方之和作为损失函数来衡量降维带来的误差（类似于误差平方和损失函数SSE）。

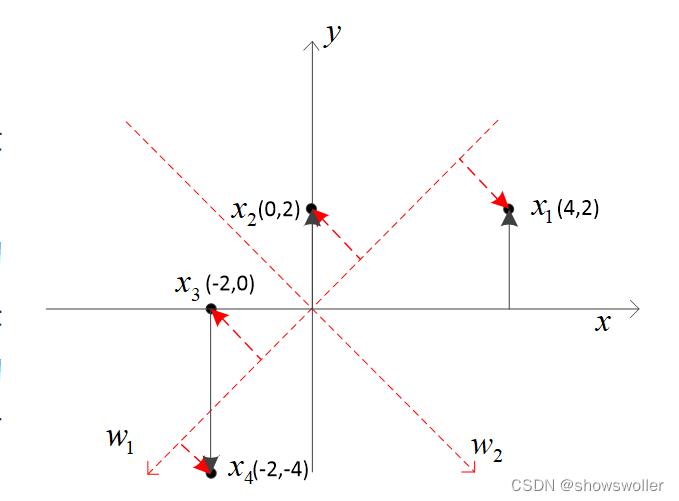
 现在要将四个点从二维降到一维，一个很自然的想法是直接去掉每个点的一个坐标，试着同步旋转X值和Y值，使得去掉Y轴上的坐标带来的损失函数最小。

只旋转不降维的输出结果如下

代码如下

from sklearn.decomposition import PCA

pca = PCA(n_components=2) # 只旋转不降维
pca.fit(x)
print("新的轴向量：")
print(pca.components_)
print("各维度投影方差占比分布：")
print(pca.explained_variance_ratio_)
print("各点在新轴上的投影：")
print(pca.transform(x))

 降到一维的结果如下

代码如下

pca = PCA(n_components=1) # 降到一维
pca.fit(x)
print("新的轴向量：")
print(pca.components_)
print("各维度投影方差占比分布：")
print(pca.explained_variance_ratio_)
print("各点在新轴上的投影：")
print(pca.transform(x))

2：三维数据可视化降维

我们生成三维空间中分布的点，然后降到二维

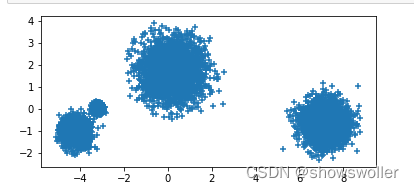
在三维空间中生成四个簇，并查看它们的分布如下

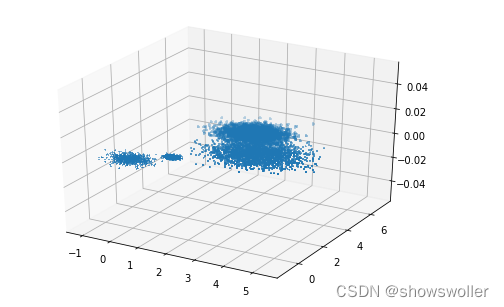
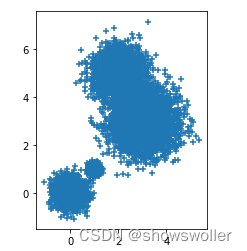
 接下来我们分布查看它们在三个面上的投影 可以看出每个面上的投影都有两个簇重叠的情况

 

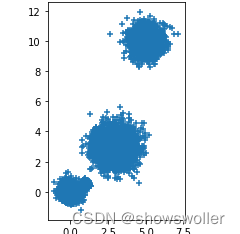
 接着用PCA对它们进行降维，共进行了三次，第一次降到一个二维的平面上，可见可以较好的分开为四个簇，第二次要求保留百分之九十的精度，第三次要求保留百分之九十九精度，此时不能降低维数，否则就达不到该要求

结果如下

 

部分代码如下 需要全部代码请点赞关注收藏后评论区留言私信~~~

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_blobs
X, _ = make_blobs(n_samples=10000, n_features=3, centers=[[0,0,0], [1,1,0.5], [3,3,3], [2,5,10]], cluster_std=[0.3, 0.1, 0.7, 0.5])
fig = plt.figure()
ax = Axes3D(fig)
plt.scatter(X[:, 0], X[:, 1], X[:, 2], marker='+')

创作不易 觉得有帮助请点赞关注收藏~~